Coupled Input-Output Dimension Reduction: Application to Goal-oriented Bayesian Experimental Design and Global Sensitivity Analysis

We introduce a new method to jointly reduce the dimension of the input and output space of a high-dimensional function. Choosing a reduced input subspace influences which output subspace is relevant and vice versa. Conventional methods focus on reducing either the input or output space, even though both are often reduced simultaneously in practice. Our coupled approach naturally supports goal-oriented dimension reduction, where either an input or output quantity of interest is prescribed. We consider, in particular, goal-oriented sensor placement and goal-oriented sensitivity analysis, which can be viewed as dimension reduction where the most important output or, respectively, input components are chosen. Both applications present difficult combinatorial optimization problems with expensive objectives such as the expected information gain and Sobol indices. By optimizing gradient-based bounds, we can determine the most informative sensors and most sensitive parameters as the largest diagonal entries of some diagnostic matrices, thus bypassing the combinatorial optimization and objective evaluation.

Sharp detection of low-dimensional structure in probability measures via dimensional logarithmic Sobolev inequalities

Identifying low-dimensional structure in high-dimensional probability measures is an essential pre-processing step for efficient sampling. We introduce a method for identifying and approximating a target measure $\pi$ as a perturbation of a given reference measure $\mu$ along a few significant directions of $\mathbb{R}^{d}$. The reference measure can be a Gaussian or a nonlinear transformation of a Gaussian, as commonly arising in generative modeling. Our method extends prior work on minimizing majorizations of the Kullback--Leibler divergence to identify optimal approximations within this class of measures. Our main contribution unveils a connection between the \emph{dimensional} logarithmic Sobolev inequality (LSI) and approximations with this ansatz. Specifically, when the target and reference are both Gaussian, we show that minimizing the dimensional LSI is equivalent to minimizing the KL divergence restricted to this ansatz. For general non-Gaussian measures, the dimensional LSI produces majorants that uniformly improve on previous majorants for gradient-based dimension reduction. We further demonstrate the applicability of this analysis to the squared Hellinger distance, where analogous reasoning shows that the dimensional Poincar\'e inequality offers improved bounds.

Sequential transport maps using SoS density estimation and $α$-divergences

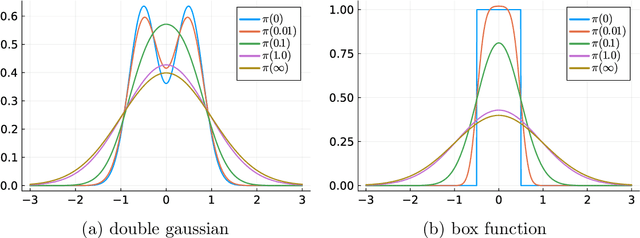
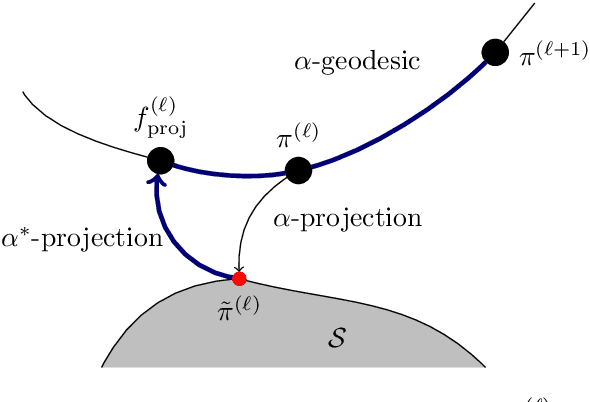
Transport-based density estimation methods are receiving growing interest because of their ability to efficiently generate samples from the approximated density. We further invertigate the sequential transport maps framework proposed from arXiv:2106.04170 arXiv:2303.02554, which builds on a sequence of composed Knothe-Rosenblatt (KR) maps. Each of those maps are built by first estimating an intermediate density of moderate complexity, and then by computing the exact KR map from a reference density to the precomputed approximate density. In our work, we explore the use of Sum-of-Squares (SoS) densities and $\alpha$-divergences for approximating the intermediate densities. Combining SoS densities with $\alpha$-divergence interestingly yields convex optimization problems which can be efficiently solved using semidefinite programming. The main advantage of $\alpha$-divergences is to enable working with unnormalized densities, which provides benefits both numerically and theoretically. In particular, we provide two new convergence analyses of the sequential transport maps: one based on a triangle-like inequality and the second on information geometric properties of $\alpha$-divergences for unnormalizied densities. The choice of intermediate densities is also crucial for the efficiency of the method. While tempered (or annealed) densities are the state-of-the-art, we introduce diffusion-based intermediate densities which permits to approximate densities known from samples only. Such intermediate densities are well-established in machine learning for generative modeling. Finally we propose and try different low-dimensional maps (or lazy maps) for dealing with high-dimensional problems and numerically demonstrate our methods on several benchmarks, including Bayesian inference problems and unsupervised learning task.

Self-reinforced polynomial approximation methods for concentrated probability densities

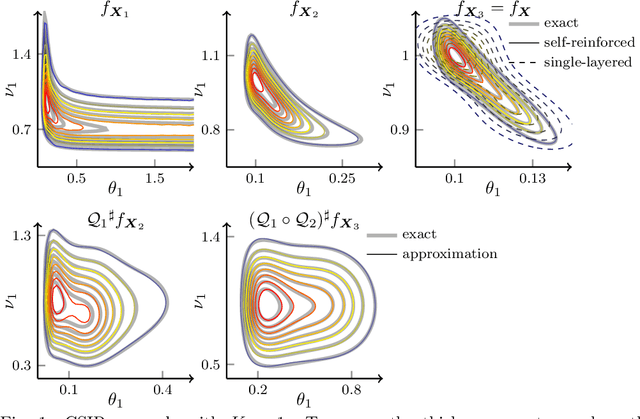
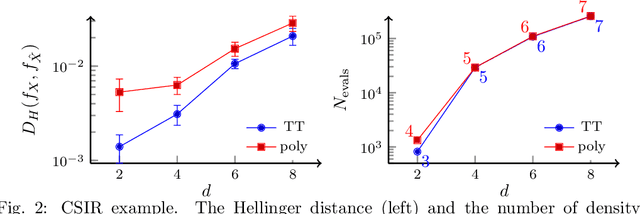
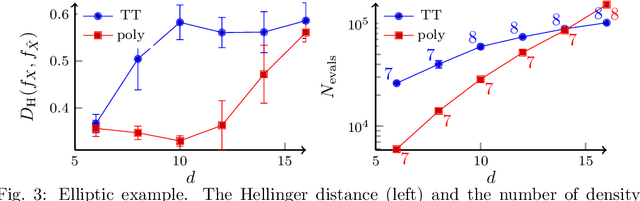
Transport map methods offer a powerful statistical learning tool that can couple a target high-dimensional random variable with some reference random variable using invertible transformations. This paper presents new computational techniques for building the Knothe--Rosenblatt (KR) rearrangement based on general separable functions. We first introduce a new construction of the KR rearrangement -- with guaranteed invertibility in its numerical implementation -- based on approximating the density of the target random variable using tensor-product spectral polynomials and downward closed sparse index sets. Compared to other constructions of KR arrangements based on either multi-linear approximations or nonlinear optimizations, our new construction only relies on a weighted least square approximation procedure. Then, inspired by the recently developed deep tensor trains (Cui and Dolgov, Found. Comput. Math. 22:1863--1922, 2022), we enhance the approximation power of sparse polynomials by preconditioning the density approximation problem using compositions of maps. This is particularly suitable for high-dimensional and concentrated probability densities commonly seen in many applications. We approximate the complicated target density by a composition of self-reinforced KR rearrangements, in which previously constructed KR rearrangements -- based on the same approximation ansatz -- are used to precondition the density approximation problem for building each new KR rearrangement. We demonstrate the efficiency of our proposed methods and the importance of using the composite map on several inverse problems governed by ordinary differential equations (ODEs) and partial differential equations (PDEs).

Conditional Deep Inverse Rosenblatt Transports

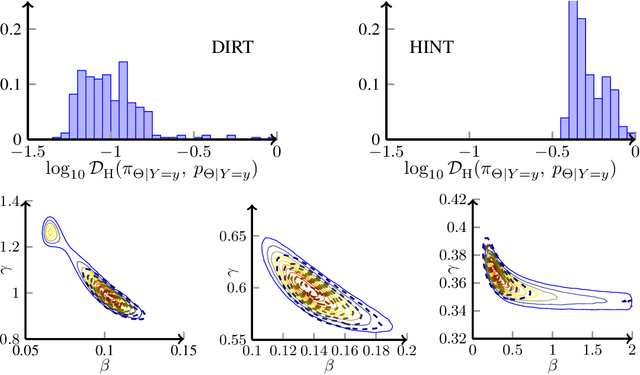
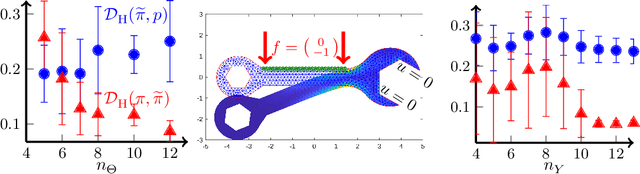
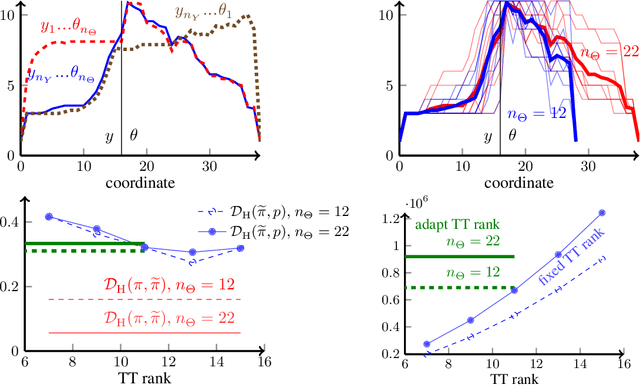
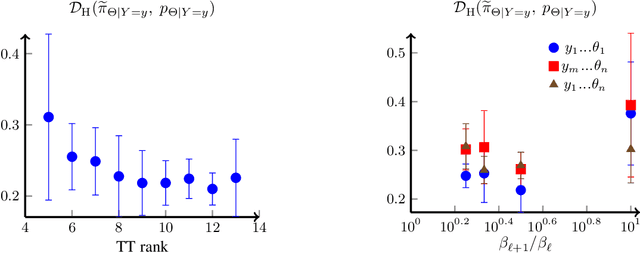
We present a novel offline-online method to mitigate the computational burden of the characterization of conditional beliefs in statistical learning. In the offline phase, the proposed method learns the joint law of the belief random variables and the observational random variables in the tensor-train (TT) format. In the online phase, it utilizes the resulting order-preserving conditional transport map to issue real-time characterization of the conditional beliefs given new observed information. Compared with the state-of-the-art normalizing flows techniques, the proposed method relies on function approximation and is equipped with thorough performance analysis. This also allows us to further extend the capability of transport maps in challenging problems with high-dimensional observations and high-dimensional belief variables. On the one hand, we present novel heuristics to reorder and/or reparametrize the variables to enhance the approximation power of TT. On the other, we integrate the TT-based transport maps and the parameter reordering/reparametrization into layered compositions to further improve the performance of the resulting transport maps. We demonstrate the efficiency of the proposed method on various statistical learning tasks in ordinary differential equations (ODEs) and partial differential equations (PDEs).

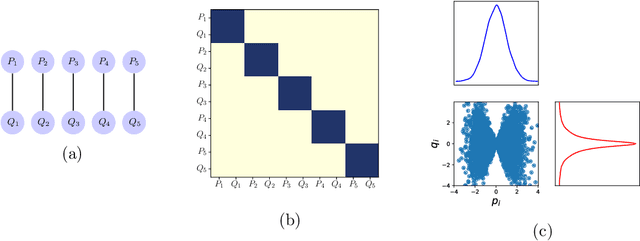
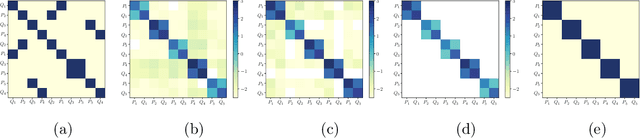
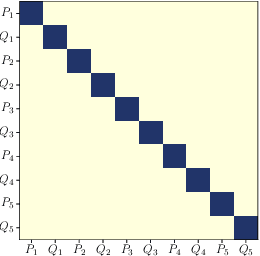
Learning non-Gaussian graphical models via Hessian scores and triangular transport

Undirected probabilistic graphical models represent the conditional dependencies, or Markov properties, of a collection of random variables. Knowing the sparsity of such a graphical model is valuable for modeling multivariate distributions and for efficiently performing inference. While the problem of learning graph structure from data has been studied extensively for certain parametric families of distributions, most existing methods fail to consistently recover the graph structure for non-Gaussian data. Here we propose an algorithm for learning the Markov structure of continuous and non-Gaussian distributions. To characterize conditional independence, we introduce a score based on integrated Hessian information from the joint log-density, and we prove that this score upper bounds the conditional mutual information for a general class of distributions. To compute the score, our algorithm SING estimates the density using a deterministic coupling, induced by a triangular transport map, and iteratively exploits sparse structure in the map to reveal sparsity in the graph. For certain non-Gaussian datasets, we show that our algorithm recovers the graph structure even with a biased approximation to the density. Among other examples, we apply sing to learn the dependencies between the states of a chaotic dynamical system with local interactions.

An adaptive transport framework for joint and conditional density estimation

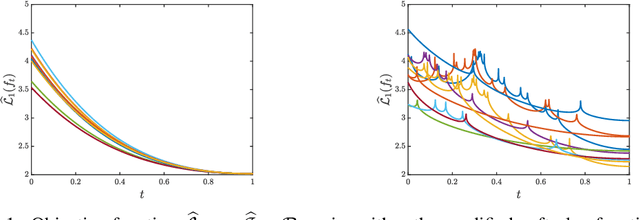
We propose a general framework to robustly characterize joint and conditional probability distributions via transport maps. Transport maps or "flows" deterministically couple two distributions via an expressive monotone transformation. Yet, learning the parameters of such transformations in high dimensions is challenging given few samples from the unknown target distribution, and structural choices for these transformations can have a significant impact on performance. Here we formulate a systematic framework for representing and learning monotone maps, via invertible transformations of smooth functions, and demonstrate that the associated minimization problem has a unique global optimum. Given a hierarchical basis for the appropriate function space, we propose a sample-efficient adaptive algorithm that estimates a sparse approximation for the map. We demonstrate how this framework can learn densities with stable generalization performance across a wide range of sample sizes on real-world datasets.

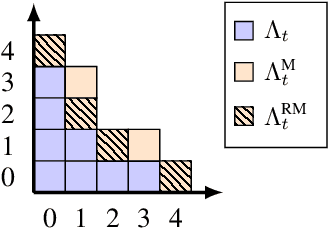
Greedy inference with layers of lazy maps

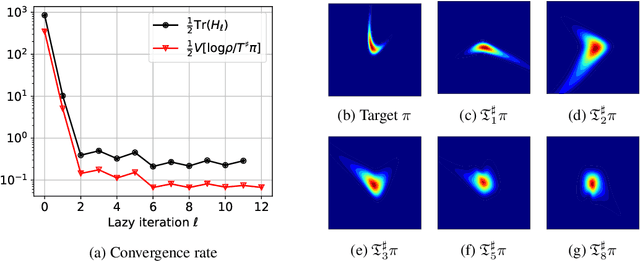
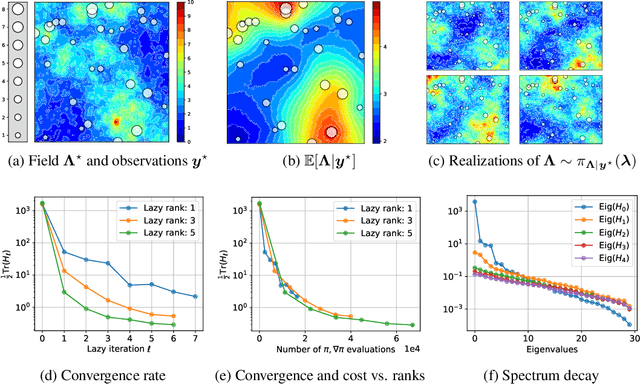
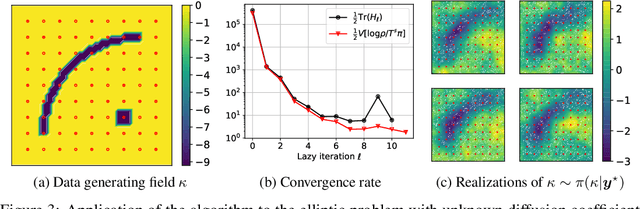
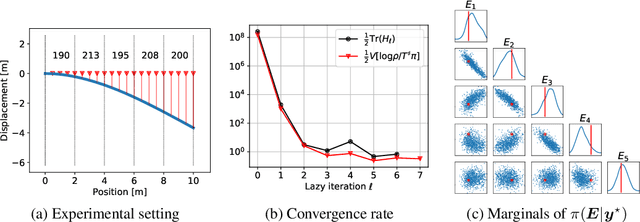
We propose a framework for the greedy approximation of high-dimensional Bayesian inference problems, through the composition of multiple \emph{low-dimensional} transport maps or flows. Our framework operates recursively on a sequence of ``residual'' distributions, given by pulling back the posterior through the previously computed transport maps. The action of each map is confined to a low-dimensional subspace that we identify by minimizing an error bound. At each step, our approach thus identifies (i) a relevant subspace of the residual distribution, and (ii) a low-dimensional transformation between a restriction of the residual onto this subspace and a standard Gaussian. We prove weak convergence of the approach to the posterior distribution, and we demonstrate the algorithm on a range of challenging inference problems in differential equations and spatial statistics.