Coupling techniques for nonlinear ensemble filtering

We consider filtering in high-dimensional non-Gaussian state-space models with intractable transition kernels, nonlinear and possibly chaotic dynamics, and sparse observations in space and time. We propose a novel filtering methodology that harnesses transportation of measures, convex optimization, and ideas from probabilistic graphical models to yield robust ensemble approximations of the filtering distribution in high dimensions. Our approach can be understood as the natural generalization of the ensemble Kalman filter (EnKF) to nonlinear updates, using stochastic or deterministic couplings. The use of nonlinear updates can reduce the intrinsic bias of the EnKF at a marginal increase in computational cost. We avoid any form of importance sampling and introduce non-Gaussian localization approaches for dimension scalability. Our framework achieves state-of-the-art tracking performance on challenging configurations of the Lorenz-96 model in the chaotic regime.

Greedy inference with layers of lazy maps

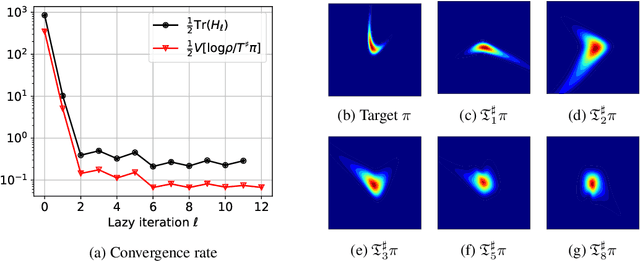
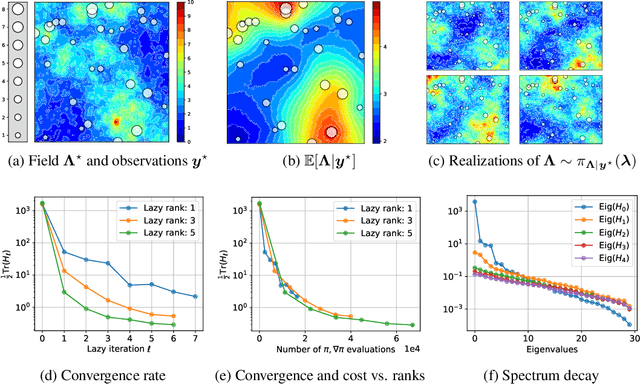
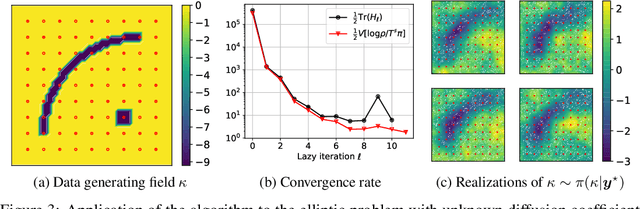
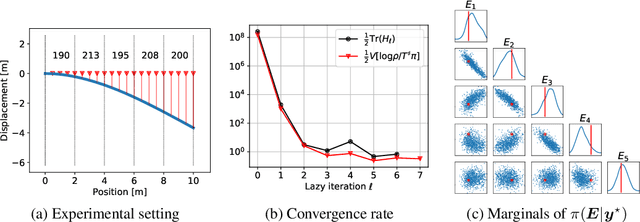
We propose a framework for the greedy approximation of high-dimensional Bayesian inference problems, through the composition of multiple \emph{low-dimensional} transport maps or flows. Our framework operates recursively on a sequence of ``residual'' distributions, given by pulling back the posterior through the previously computed transport maps. The action of each map is confined to a low-dimensional subspace that we identify by minimizing an error bound. At each step, our approach thus identifies (i) a relevant subspace of the residual distribution, and (ii) a low-dimensional transformation between a restriction of the residual onto this subspace and a standard Gaussian. We prove weak convergence of the approach to the posterior distribution, and we demonstrate the algorithm on a range of challenging inference problems in differential equations and spatial statistics.

A Stein variational Newton method

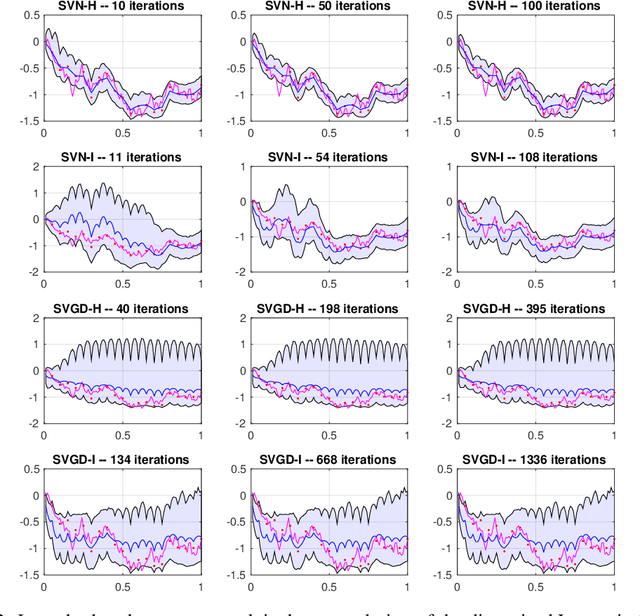
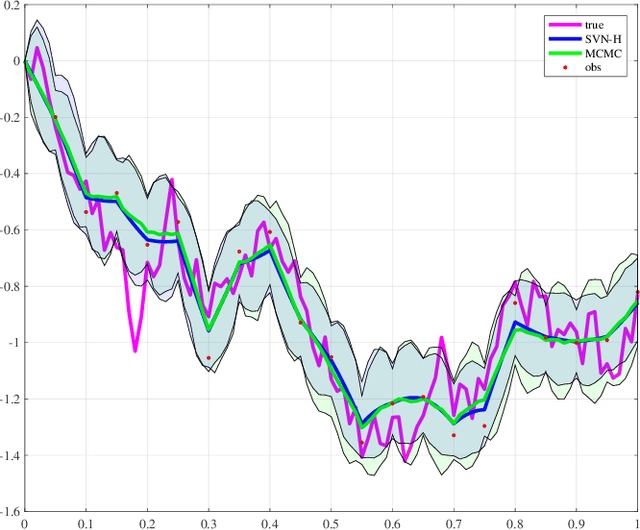
Stein variational gradient descent (SVGD) was recently proposed as a general purpose nonparametric variational inference algorithm [Liu & Wang, NIPS 2016]: it minimizes the Kullback-Leibler divergence between the target distribution and its approximation by implementing a form of functional gradient descent on a reproducing kernel Hilbert space. In this paper, we accelerate and generalize the SVGD algorithm by including second-order information, thereby approximating a Newton-like iteration in function space. We also show how second-order information can lead to more effective choices of kernel. We observe significant computational gains over the original SVGD algorithm in multiple test cases.

Inference via low-dimensional couplings

We investigate the low-dimensional structure of deterministic transformations between random variables, i.e., transport maps between probability measures. In the context of statistics and machine learning, these transformations can be used to couple a tractable "reference" measure (e.g., a standard Gaussian) with a target measure of interest. Direct simulation from the desired measure can then be achieved by pushing forward reference samples through the map. Yet characterizing such a map---e.g., representing and evaluating it---grows challenging in high dimensions. The central contribution of this paper is to establish a link between the Markov properties of the target measure and the existence of low-dimensional couplings, induced by transport maps that are sparse and/or decomposable. Our analysis not only facilitates the construction of transformations in high-dimensional settings, but also suggests new inference methodologies for continuous non-Gaussian graphical models. For instance, in the context of nonlinear state-space models, we describe new variational algorithms for filtering, smoothing, and sequential parameter inference. These algorithms can be understood as the natural generalization---to the non-Gaussian case---of the square-root Rauch-Tung-Striebel Gaussian smoother.