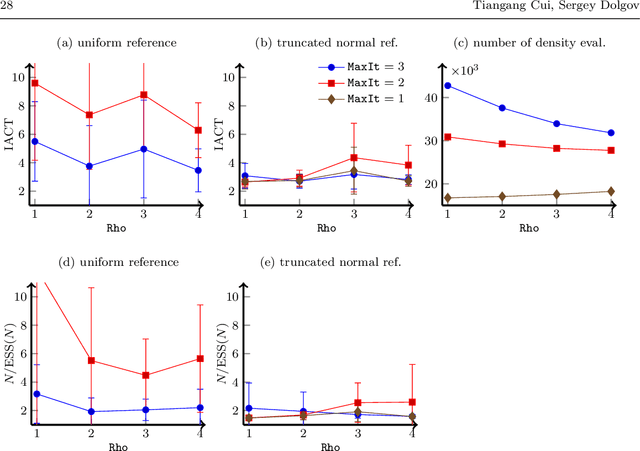
Tiangang Cui
Low-rank Bayesian matrix completion via geodesic Hamiltonian Monte Carlo on Stiefel manifolds
Oct 27, 2024
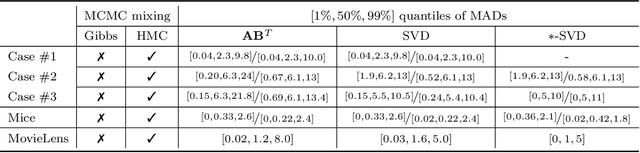
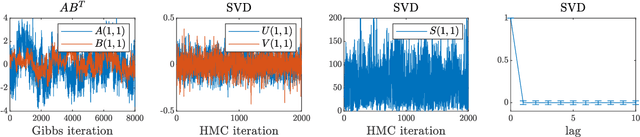
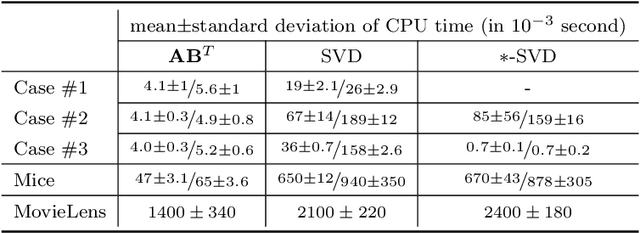
Abstract:We present a new sampling-based approach for enabling efficient computation of low-rank Bayesian matrix completion and quantifying the associated uncertainty. Firstly, we design a new prior model based on the singular-value-decomposition (SVD) parametrization of low-rank matrices. Our prior is analogous to the seminal nuclear-norm regularization used in non-Bayesian setting and enforces orthogonality in the factor matrices by constraining them to Stiefel manifolds. Then, we design a geodesic Hamiltonian Monte Carlo (-within-Gibbs) algorithm for generating posterior samples of the SVD factor matrices. We demonstrate that our approach resolves the sampling difficulties encountered by standard Gibbs samplers for the common two-matrix factorization used in matrix completion. More importantly, the geodesic Hamiltonian sampler allows for sampling in cases with more general likelihoods than the typical Gaussian likelihood and Gaussian prior assumptions adopted in most of the existing Bayesian matrix completion literature. We demonstrate an applications of our approach to fit the categorical data of a mice protein dataset and the MovieLens recommendation problem. Numerical examples demonstrate superior sampling performance, including better mixing and faster convergence to a stationary distribution. Moreover, they demonstrate improved accuracy on the two real-world benchmark problems we considered.
l_inf-approximation of localized distributions
Oct 15, 2024Abstract:Distributions in spatial model often exhibit localized features. Intuitively, this locality implies a low intrinsic dimensionality, which can be exploited for efficient approximation and computation of complex distributions. However, existing approximation theory mainly considers the joint distributions, which does not guarantee that the marginal errors are small. In this work, we establish a dimension independent error bound for the marginals of approximate distributions. This $\ell_\infty$-approximation error is obtained using Stein's method, and we propose a $\delta$-locality condition that quantifies the degree of localization in a distribution. We also show how $\delta$-locality can be derived from different conditions that characterize the distribution's locality. Our $\ell_\infty$ bound motivates the localization of existing approximation methods to respect the locality. As examples, we show how to use localized likelihood-informed subspace method and localized score matching, which not only avoid dimension dependence in the approximation error, but also significantly reduce the computational cost due to the local and parallel implementation based on the localized structure.
Sharp detection of low-dimensional structure in probability measures via dimensional logarithmic Sobolev inequalities
Jun 18, 2024Abstract:Identifying low-dimensional structure in high-dimensional probability measures is an essential pre-processing step for efficient sampling. We introduce a method for identifying and approximating a target measure $\pi$ as a perturbation of a given reference measure $\mu$ along a few significant directions of $\mathbb{R}^{d}$. The reference measure can be a Gaussian or a nonlinear transformation of a Gaussian, as commonly arising in generative modeling. Our method extends prior work on minimizing majorizations of the Kullback--Leibler divergence to identify optimal approximations within this class of measures. Our main contribution unveils a connection between the \emph{dimensional} logarithmic Sobolev inequality (LSI) and approximations with this ansatz. Specifically, when the target and reference are both Gaussian, we show that minimizing the dimensional LSI is equivalent to minimizing the KL divergence restricted to this ansatz. For general non-Gaussian measures, the dimensional LSI produces majorants that uniformly improve on previous majorants for gradient-based dimension reduction. We further demonstrate the applicability of this analysis to the squared Hellinger distance, where analogous reasoning shows that the dimensional Poincar\'e inequality offers improved bounds.
Sequential transport maps using SoS density estimation and $α$-divergences
Feb 27, 2024

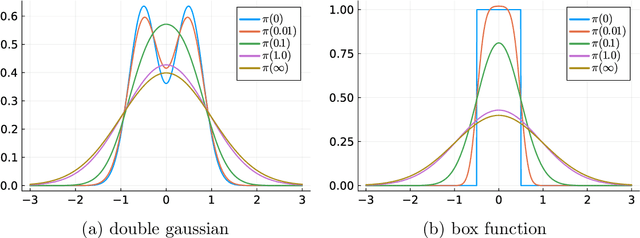
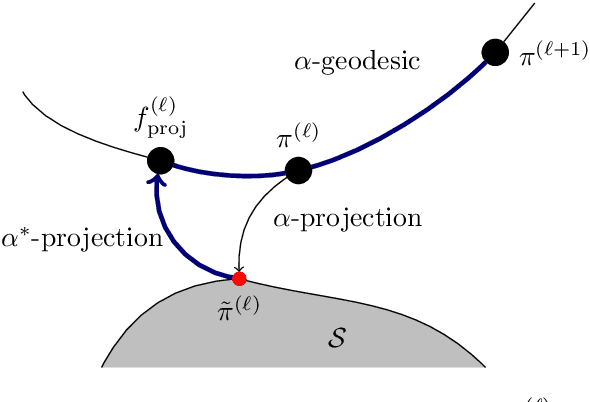
Abstract:Transport-based density estimation methods are receiving growing interest because of their ability to efficiently generate samples from the approximated density. We further invertigate the sequential transport maps framework proposed from arXiv:2106.04170 arXiv:2303.02554, which builds on a sequence of composed Knothe-Rosenblatt (KR) maps. Each of those maps are built by first estimating an intermediate density of moderate complexity, and then by computing the exact KR map from a reference density to the precomputed approximate density. In our work, we explore the use of Sum-of-Squares (SoS) densities and $\alpha$-divergences for approximating the intermediate densities. Combining SoS densities with $\alpha$-divergence interestingly yields convex optimization problems which can be efficiently solved using semidefinite programming. The main advantage of $\alpha$-divergences is to enable working with unnormalized densities, which provides benefits both numerically and theoretically. In particular, we provide two new convergence analyses of the sequential transport maps: one based on a triangle-like inequality and the second on information geometric properties of $\alpha$-divergences for unnormalizied densities. The choice of intermediate densities is also crucial for the efficiency of the method. While tempered (or annealed) densities are the state-of-the-art, we introduce diffusion-based intermediate densities which permits to approximate densities known from samples only. Such intermediate densities are well-established in machine learning for generative modeling. Finally we propose and try different low-dimensional maps (or lazy maps) for dealing with high-dimensional problems and numerically demonstrate our methods on several benchmarks, including Bayesian inference problems and unsupervised learning task.
Self-reinforced polynomial approximation methods for concentrated probability densities
Mar 05, 2023
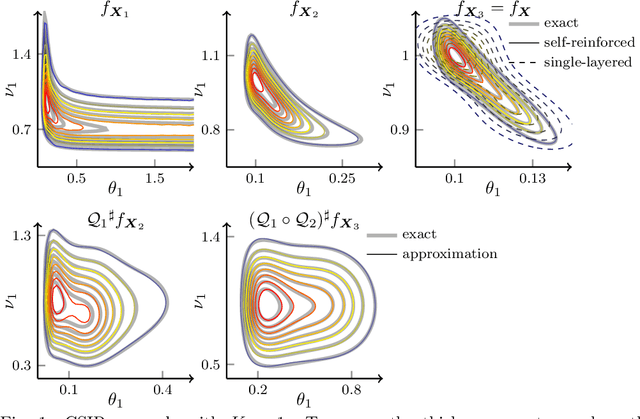
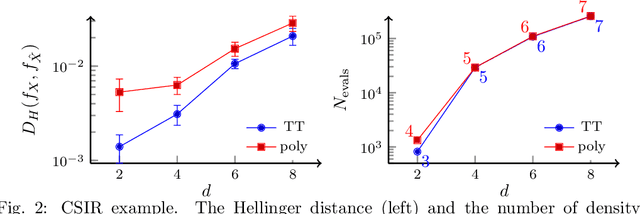
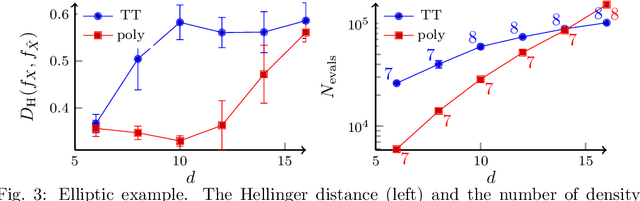
Abstract:Transport map methods offer a powerful statistical learning tool that can couple a target high-dimensional random variable with some reference random variable using invertible transformations. This paper presents new computational techniques for building the Knothe--Rosenblatt (KR) rearrangement based on general separable functions. We first introduce a new construction of the KR rearrangement -- with guaranteed invertibility in its numerical implementation -- based on approximating the density of the target random variable using tensor-product spectral polynomials and downward closed sparse index sets. Compared to other constructions of KR arrangements based on either multi-linear approximations or nonlinear optimizations, our new construction only relies on a weighted least square approximation procedure. Then, inspired by the recently developed deep tensor trains (Cui and Dolgov, Found. Comput. Math. 22:1863--1922, 2022), we enhance the approximation power of sparse polynomials by preconditioning the density approximation problem using compositions of maps. This is particularly suitable for high-dimensional and concentrated probability densities commonly seen in many applications. We approximate the complicated target density by a composition of self-reinforced KR rearrangements, in which previously constructed KR rearrangements -- based on the same approximation ansatz -- are used to precondition the density approximation problem for building each new KR rearrangement. We demonstrate the efficiency of our proposed methods and the importance of using the composite map on several inverse problems governed by ordinary differential equations (ODEs) and partial differential equations (PDEs).
A variational neural network approach for glacier modelling with nonlinear rheology
Sep 05, 2022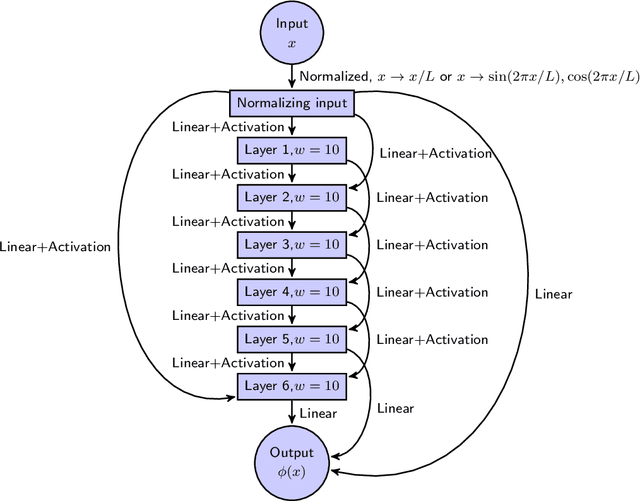
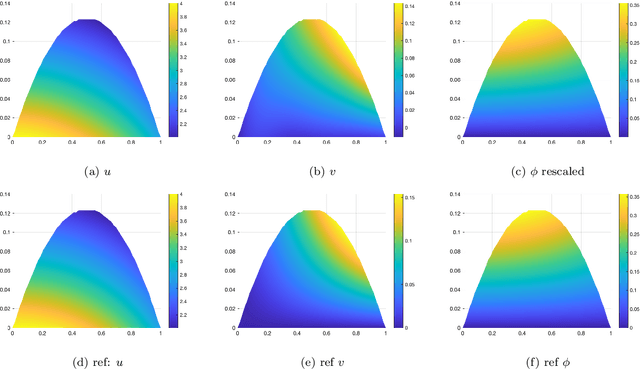
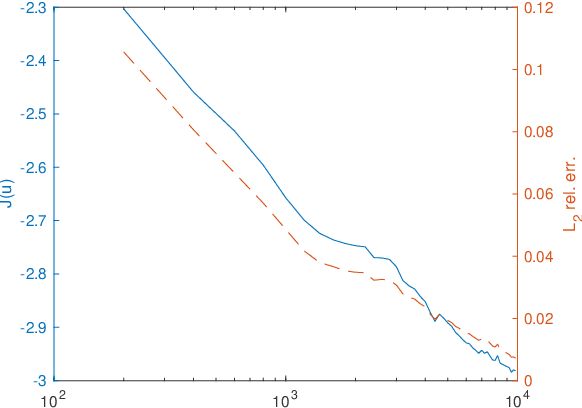
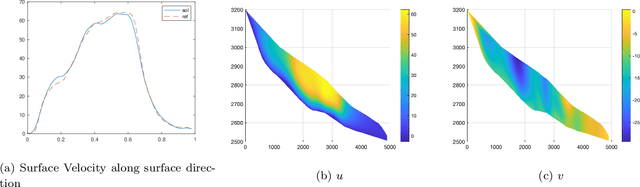
Abstract:In this paper, we propose a mesh-free method to solve full stokes equation which models the glacier movement with nonlinear rheology. Our approach is inspired by the Deep-Ritz method proposed in [12]. We first formulate the solution of non-Newtonian ice flow model into the minimizer of a variational integral with boundary constraints. The solution is then approximated by a deep neural network whose loss function is the variational integral plus soft constraint from the mixed boundary conditions. Instead of introducing mesh grids or basis functions to evaluate the loss function, our method only requires uniform samplers of the domain and boundaries. To address instability in real-world scaling, we re-normalize the input of the network at the first layer and balance the regularizing factors for each individual boundary. Finally, we illustrate the performance of our method by several numerical experiments, including a 2D model with analytical solution, Arolla glacier model with real scaling and a 3D model with periodic boundary conditions. Numerical results show that our proposed method is efficient in solving the non-Newtonian mechanics arising from glacier modeling with nonlinear rheology.
Deep importance sampling using tensor-trains with application to a priori and a posteriori rare event estimation
Sep 05, 2022



Abstract:We propose a deep importance sampling method that is suitable for estimating rare event probabilities in high-dimensional problems. We approximate the optimal importance distribution in a general importance sampling problem as the pushforward of a reference distribution under a composition of order-preserving transformations, in which each transformation is formed by a squared tensor-train decomposition. The squared tensor-train decomposition provides a scalable ansatz for building order-preserving high-dimensional transformations via density approximations. The use of composition of maps moving along a sequence of bridging densities alleviates the difficulty of directly approximating concentrated density functions. To compute expectations over unnormalized probability distributions, we design a ratio estimator that estimates the normalizing constant using a separate importance distribution, again constructed via a composition of transformations in tensor-train format. This offers better theoretical variance reduction compared with self-normalized importance sampling, and thus opens the door to efficient computation of rare event probabilities in Bayesian inference problems. Numerical experiments on problems constrained by differential equations show little to no increase in the computational complexity with the event probability going to zero, and allow to compute hitherto unattainable estimates of rare event probabilities for complex, high-dimensional posterior densities.
Conditional Deep Inverse Rosenblatt Transports
Jun 08, 2021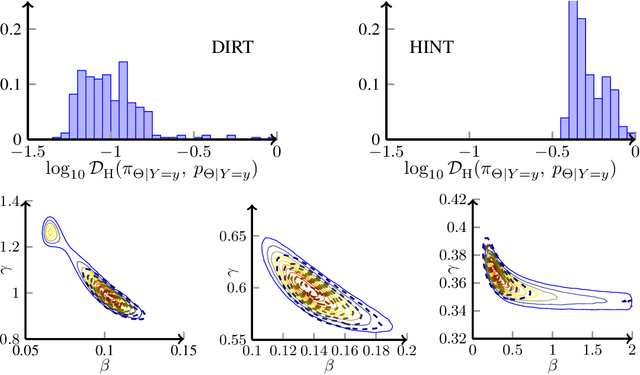
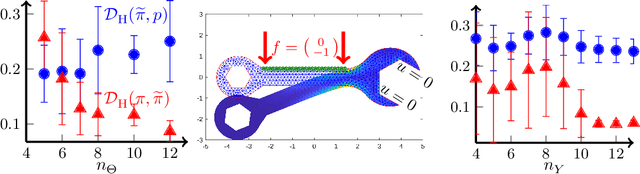
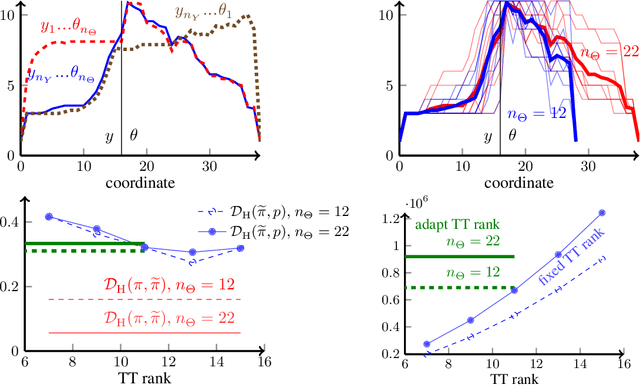
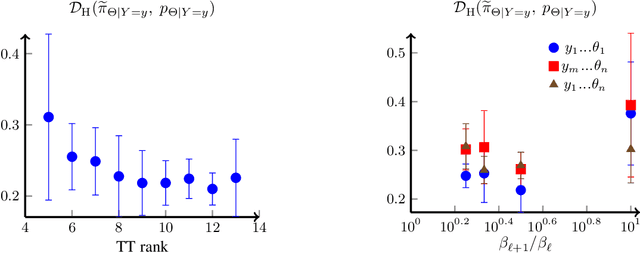
Abstract:We present a novel offline-online method to mitigate the computational burden of the characterization of conditional beliefs in statistical learning. In the offline phase, the proposed method learns the joint law of the belief random variables and the observational random variables in the tensor-train (TT) format. In the online phase, it utilizes the resulting order-preserving conditional transport map to issue real-time characterization of the conditional beliefs given new observed information. Compared with the state-of-the-art normalizing flows techniques, the proposed method relies on function approximation and is equipped with thorough performance analysis. This also allows us to further extend the capability of transport maps in challenging problems with high-dimensional observations and high-dimensional belief variables. On the one hand, we present novel heuristics to reorder and/or reparametrize the variables to enhance the approximation power of TT. On the other, we integrate the TT-based transport maps and the parameter reordering/reparametrization into layered compositions to further improve the performance of the resulting transport maps. We demonstrate the efficiency of the proposed method on various statistical learning tasks in ordinary differential equations (ODEs) and partial differential equations (PDEs).
Identification of brain states, transitions, and communities using functional MRI
Jan 26, 2021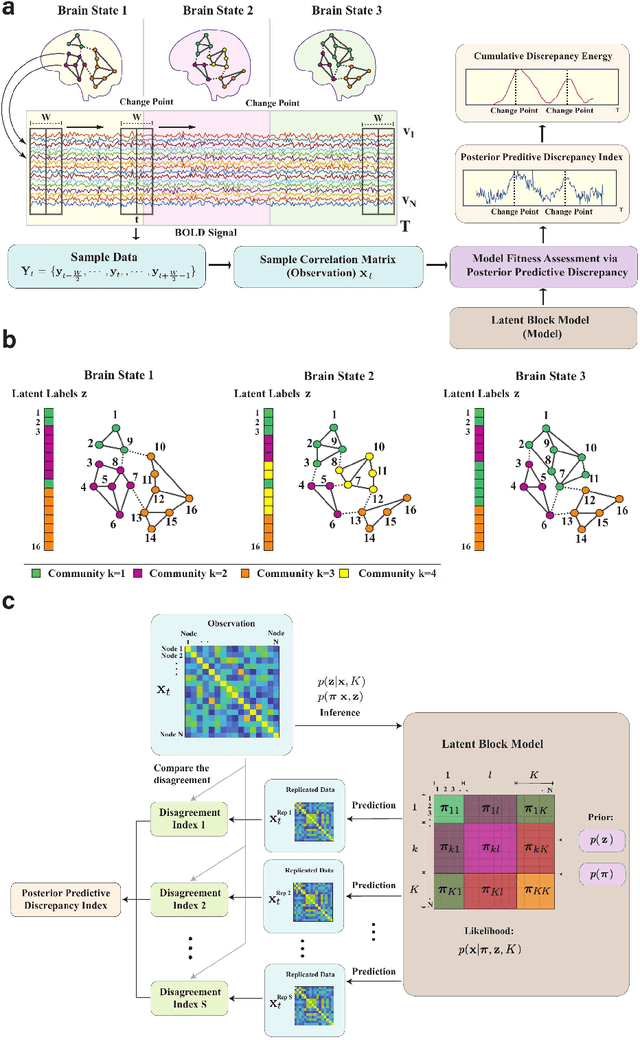
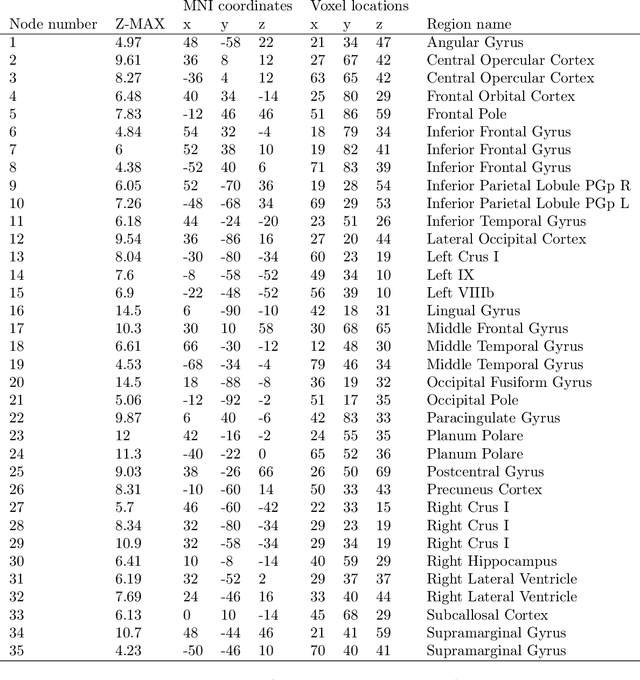
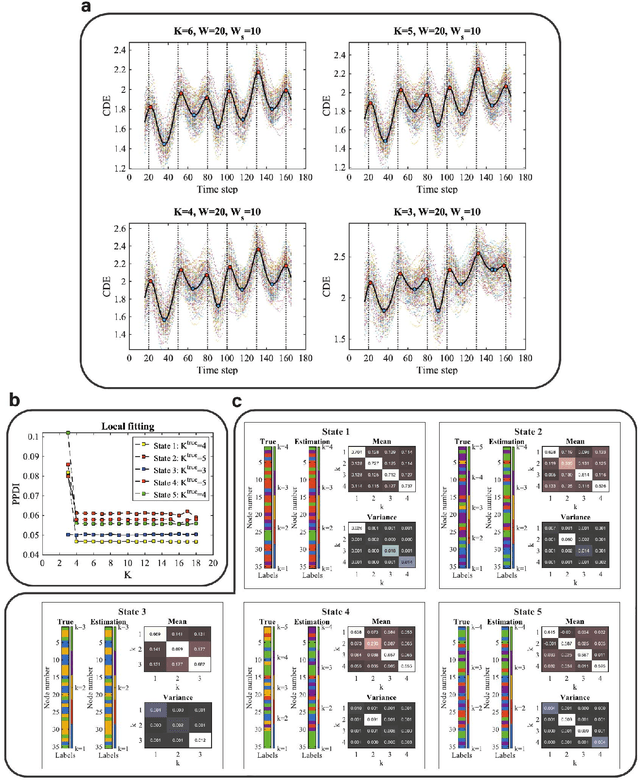

Abstract:Brain function relies on a precisely coordinated and dynamic balance between the functional integration and segregation of distinct neural systems. Characterizing the way in which neural systems reconfigure their interactions to give rise to distinct but hidden brain states remains an open challenge. In this paper, we propose a Bayesian model-based characterization of latent brain states and showcase a novel method based on posterior predictive discrepancy using the latent block model to detect transitions between latent brain states in blood oxygen level-dependent (BOLD) time series. The set of estimated parameters in the model includes a latent label vector that assigns network nodes to communities, and also block model parameters that reflect the weighted connectivity within and between communities. Besides extensive in-silico model evaluation, we also provide empirical validation (and replication) using the Human Connectome Project (HCP) dataset of 100 healthy adults. Our results obtained through an analysis of task-fMRI data during working memory performance show appropriate lags between external task demands and change-points between brain states, with distinctive community patterns distinguishing fixation, low-demand and high-demand task conditions.
Deep Composition of Tensor Trains using Squared Inverse Rosenblatt Transports
Jul 14, 2020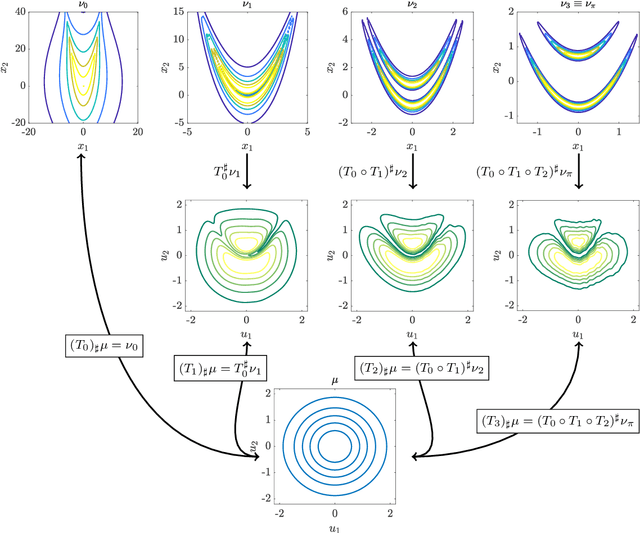
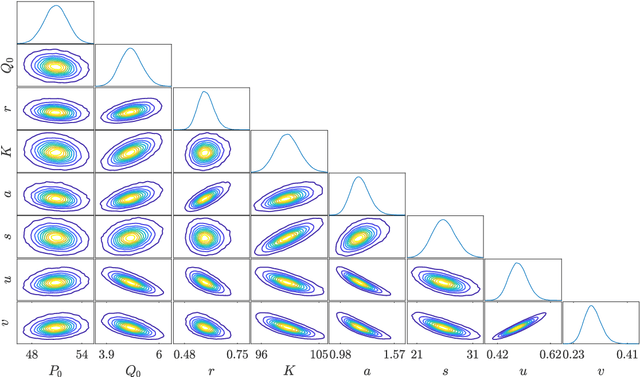

Abstract:Characterising intractable high-dimensional random variables is one of the fundamental challenges in stochastic computation. The recent surge of transport maps offers a mathematical foundation and new insights for tackling this challenge by coupling intractable random variables with tractable reference random variables. This paper generalises a recently developed functional tensor-train (FTT) approximation of the inverse Rosenblatt transport [14] to a wide class of high-dimensional nonnegative functions, such as unnormalised probability density functions. First, we extend the inverse Rosenblatt transform to enable the transport to general reference measures other than the uniform measure. We develop an efficient procedure to compute this transport from a squared FTT decomposition which preserves the monotonicity. More crucially, we integrate the proposed monotonicity-preserving FTT transport into a nested variable transformation framework inspired by deep neural networks. The resulting deep inverse Rosenblatt transport significantly expands the capability of tensor approximations and transport maps to random variables with complicated nonlinear interactions and concentrated density functions. We demonstrate the efficacy of the proposed approach on a range of applications in statistical learning and uncertainty quantification, including parameter estimation for dynamical systems and inverse problems constrained by partial differential equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge