Global Well-posedness and Convergence Analysis of Score-based Generative Models via Sharp Lipschitz Estimates

We establish global well-posedness and convergence of the score-based generative models (SGM) under minimal general assumptions of initial data for score estimation. For the smooth case, we start from a Lipschitz bound of the score function with optimal time length. The optimality is validated by an example whose Lipschitz constant of scores is bounded at initial but blows up in finite time. This necessitates the separation of time scales in conventional bounds for non-log-concave distributions. In contrast, our follow up analysis only relies on a local Lipschitz condition and is valid globally in time. This leads to the convergence of numerical scheme without time separation. For the non-smooth case, we show that the optimal Lipschitz bound is O(1/t) in the point-wise sense for distributions supported on a compact, smooth and low-dimensional manifold with boundary.

One-Shot High-Fidelity Talking-Head Synthesis with Deformable Neural Radiance Field

Talking head generation aims to generate faces that maintain the identity information of the source image and imitate the motion of the driving image. Most pioneering methods rely primarily on 2D representations and thus will inevitably suffer from face distortion when large head rotations are encountered. Recent works instead employ explicit 3D structural representations or implicit neural rendering to improve performance under large pose changes. Nevertheless, the fidelity of identity and expression is not so desirable, especially for novel-view synthesis. In this paper, we propose HiDe-NeRF, which achieves high-fidelity and free-view talking-head synthesis. Drawing on the recently proposed Deformable Neural Radiance Fields, HiDe-NeRF represents the 3D dynamic scene into a canonical appearance field and an implicit deformation field, where the former comprises the canonical source face and the latter models the driving pose and expression. In particular, we improve fidelity from two aspects: (i) to enhance identity expressiveness, we design a generalized appearance module that leverages multi-scale volume features to preserve face shape and details; (ii) to improve expression preciseness, we propose a lightweight deformation module that explicitly decouples the pose and expression to enable precise expression modeling. Extensive experiments demonstrate that our proposed approach can generate better results than previous works. Project page: https://www.waytron.net/hidenerf/

Understanding the diffusion models by conditional expectations

This paper provide several mathematical analyses of the diffusion model in machine learning. The drift term of the backwards sampling process is represented as a conditional expectation involving the data distribution and the forward diffusion. The training process aims to find such a drift function by minimizing the mean-squared residue related to the conditional expectation. Using small-time approximations of the Green's function of the forward diffusion, we show that the analytical mean drift function in DDPM and the score function in SGM asymptotically blow up in the final stages of the sampling process for singular data distributions such as those concentrated on lower-dimensional manifolds, and is therefore difficult to approximate by a network. To overcome this difficulty, we derive a new target function and associated loss, which remains bounded even for singular data distributions. We illustrate the theoretical findings with several numerical examples.

A variational neural network approach for glacier modelling with nonlinear rheology

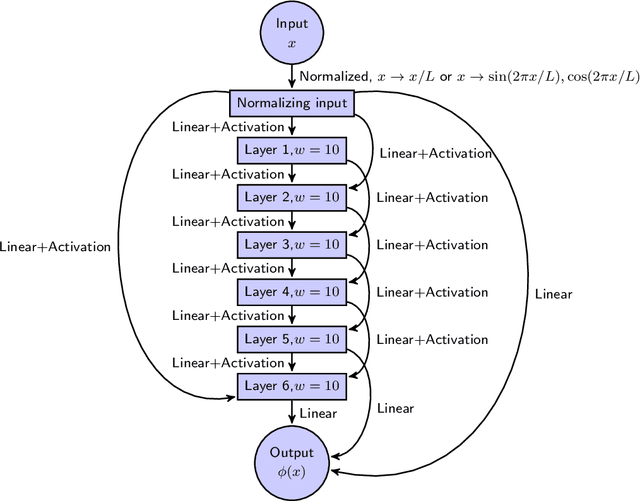
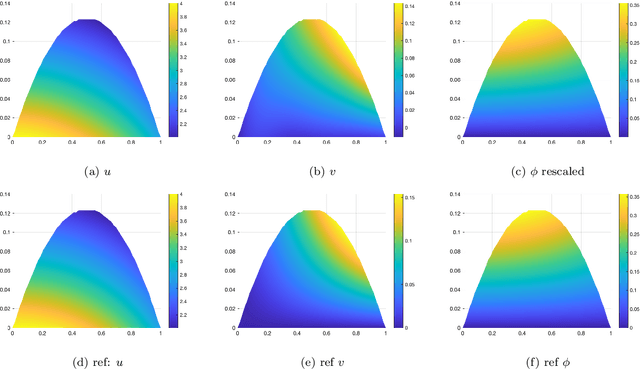
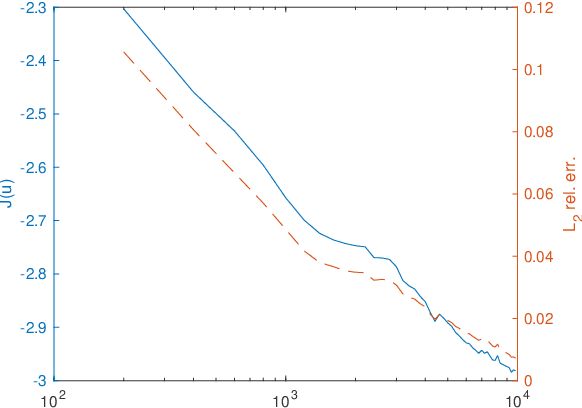
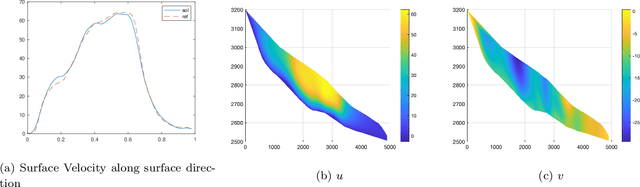
In this paper, we propose a mesh-free method to solve full stokes equation which models the glacier movement with nonlinear rheology. Our approach is inspired by the Deep-Ritz method proposed in [12]. We first formulate the solution of non-Newtonian ice flow model into the minimizer of a variational integral with boundary constraints. The solution is then approximated by a deep neural network whose loss function is the variational integral plus soft constraint from the mixed boundary conditions. Instead of introducing mesh grids or basis functions to evaluate the loss function, our method only requires uniform samplers of the domain and boundaries. To address instability in real-world scaling, we re-normalize the input of the network at the first layer and balance the regularizing factors for each individual boundary. Finally, we illustrate the performance of our method by several numerical experiments, including a 2D model with analytical solution, Arolla glacier model with real scaling and a 3D model with periodic boundary conditions. Numerical results show that our proposed method is efficient in solving the non-Newtonian mechanics arising from glacier modeling with nonlinear rheology.

DeepParticle: learning invariant measure by a deep neural network minimizing Wasserstein distance on data generated from an interacting particle method

We introduce the so called DeepParticle method to learn and generate invariant measures of stochastic dynamical systems with physical parameters based on data computed from an interacting particle method (IPM). We utilize the expressiveness of deep neural networks (DNNs) to represent the transform of samples from a given input (source) distribution to an arbitrary target distribution, neither assuming distribution functions in closed form nor a finite state space for the samples. In training, we update the network weights to minimize a discrete Wasserstein distance between the input and target samples. To reduce computational cost, we propose an iterative divide-and-conquer (a mini-batch interior point) algorithm, to find the optimal transition matrix in the Wasserstein distance. We present numerical results to demonstrate the performance of our method for accelerating IPM computation of invariant measures of stochastic dynamical systems arising in computing reaction-diffusion front speeds through chaotic flows. The physical parameter is a large Pecl\'et number reflecting the advection dominated regime of our interest.