Reservoir Computing with Error Correction: Long-term Behaviors of Stochastic Dynamical Systems

The prediction of stochastic dynamical systems and the capture of dynamical behaviors are profound problems. In this article, we propose a data-driven framework combining Reservoir Computing and Normalizing Flow to study this issue, which mimics error modeling to improve the traditional Reservoir Computing performance and takes advantage of both approaches. This model-free method successfully predicts the long-term evolution of stochastic dynamical systems and replicates dynamical behaviors. With few assumptions about the underlying stochastic dynamical systems, we deal with Markov/non-Markov and stationary/non-stationary stochastic processes defined by linear/nonlinear stochastic differential equations or stochastic delay differential equations. We verify the effectiveness of the proposed framework in five experiments, including the Ornstein-Uhlenbeck process, Double-Well system, El Ni\~no Southern Oscillation simplified model, and stochastic Lorenz system. Additionally, we explore the noise-induced tipping phenomena and the replication of the strange attractor.

Meta contrastive label correction for financial time series

Financial applications such as stock price forecasting, usually face an issue that under the predefined labeling rules, it is hard to accurately predict the directions of stock movement. This is because traditional ways of labeling, taking Triple Barrier Method, for example, usually gives us inaccurate or even corrupted labels. To address this issue, we focus on two main goals. One is that our proposed method can automatically generate correct labels for noisy time series patterns, while at the same time, the method is capable of boosting classification performance on this new labeled dataset. Based on the aforementioned goals, our approach has the following three novelties: First, we fuse a new contrastive learning algorithm into the meta-learning framework to estimate correct labels iteratively when updating the classification model inside. Moreover, we utilize images generated from time series data through Gramian angular field and representative learning. Most important of all, we adopt multi-task learning to forecast temporal-variant labels. In the experiments, we work on 6% clean data and the rest unlabeled data. It is shown that our method is competitive and outperforms a lot compared with benchmarks.

Understanding the diffusion models by conditional expectations

This paper provide several mathematical analyses of the diffusion model in machine learning. The drift term of the backwards sampling process is represented as a conditional expectation involving the data distribution and the forward diffusion. The training process aims to find such a drift function by minimizing the mean-squared residue related to the conditional expectation. Using small-time approximations of the Green's function of the forward diffusion, we show that the analytical mean drift function in DDPM and the score function in SGM asymptotically blow up in the final stages of the sampling process for singular data distributions such as those concentrated on lower-dimensional manifolds, and is therefore difficult to approximate by a network. To overcome this difficulty, we derive a new target function and associated loss, which remains bounded even for singular data distributions. We illustrate the theoretical findings with several numerical examples.

An end-to-end deep learning approach for extracting stochastic dynamical systems with $α$-stable Lévy noise

Recently, extracting data-driven governing laws of dynamical systems through deep learning frameworks has gained a lot of attention in various fields. Moreover, a growing amount of research work tends to transfer deterministic dynamical systems to stochastic dynamical systems, especially those driven by non-Gaussian multiplicative noise. However, lots of log-likelihood based algorithms that work well for Gaussian cases cannot be directly extended to non-Gaussian scenarios which could have high error and low convergence issues. In this work, we overcome some of these challenges and identify stochastic dynamical systems driven by $\alpha$-stable L\'evy noise from only random pairwise data. Our innovations include: (1) designing a deep learning approach to learn both drift and diffusion terms for L\'evy induced noise with $\alpha$ across all values, (2) learning complex multiplicative noise without restrictions on small noise intensity, (3) proposing an end-to-end complete framework for stochastic systems identification under a general input data assumption, that is, $\alpha$-stable random variable. Finally, numerical experiments and comparisons with the non-local Kramers-Moyal formulas with moment generating function confirm the effectiveness of our method.

Time Series Forecasting with Ensembled Stochastic Differential Equations Driven by Lévy Noise

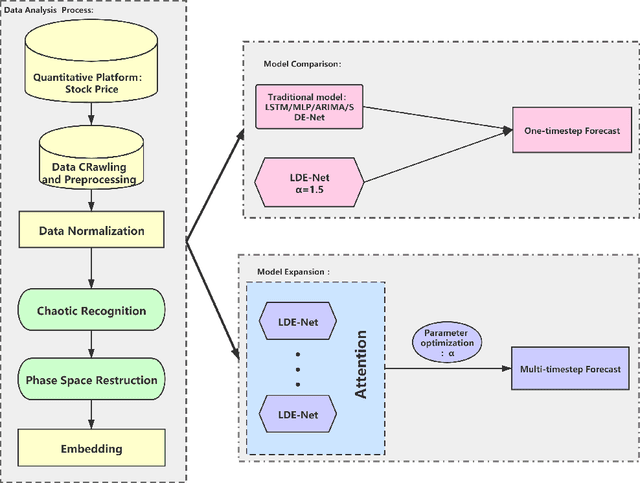
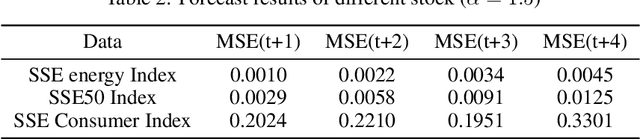
With the fast development of modern deep learning techniques, the study of dynamic systems and neural networks is increasingly benefiting each other in a lot of different ways. Since uncertainties often arise in real world observations, SDEs (stochastic differential equations) come to play an important role. To be more specific, in this paper, we use a collection of SDEs equipped with neural networks to predict long-term trend of noisy time series which has big jump properties and high probability distribution shift. Our contributions are, first, we use the phase space reconstruction method to extract intrinsic dimension of the time series data so as to determine the input structure for our forecasting model. Second, we explore SDEs driven by $\alpha$-stable L\'evy motion to model the time series data and solve the problem through neural network approximation. Third, we construct the attention mechanism to achieve multi-time step prediction. Finally, we illustrate our method by applying it to stock marketing time series prediction and show the results outperform several baseline deep learning models.

Extracting stochastic dynamical systems with $α$-stable Lévy noise from data

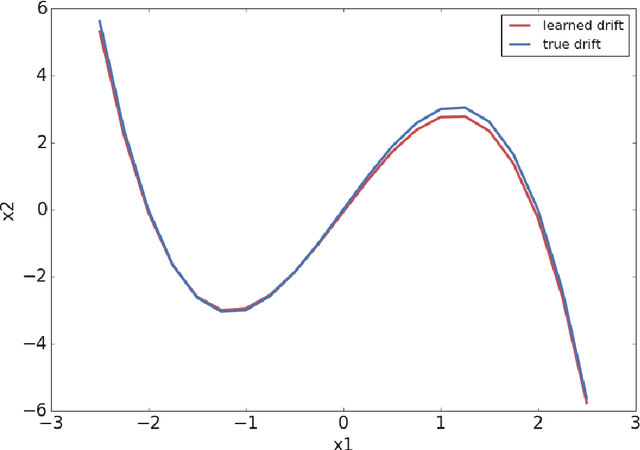
With the rapid increase of valuable observational, experimental and simulated data for complex systems, much efforts have been devoted to identifying governing laws underlying the evolution of these systems. Despite the wide applications of non-Gaussian fluctuations in numerous physical phenomena, the data-driven approaches to extract stochastic dynamical systems with (non-Gaussian) L\'evy noise are relatively few so far. In this work, we propose a data-driven method to extract stochastic dynamical systems with $\alpha$-stable L\'evy noise from short burst data based on the properties of $\alpha$-stable distributions. More specifically, we first estimate the L\'evy jump measure and noise intensity via computing mean and variance of the amplitude of the increment of the sample paths. Then we approximate the drift coefficient by combining nonlocal Kramers-Moyal formulas with normalizing flows. Numerical experiments on one- and two-dimensional prototypical examples illustrate the accuracy and effectiveness of our method. This approach will become an effective scientific tool in discovering stochastic governing laws of complex phenomena and understanding dynamical behaviors under non-Gaussian fluctuations.

Extracting Stochastic Governing Laws by Nonlocal Kramers-Moyal Formulas

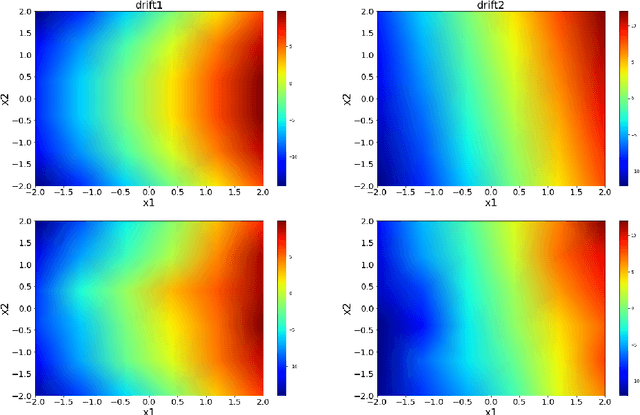
With the rapid development of computational techniques and scientific tools, great progress of data-driven analysis has been made to extract governing laws of dynamical systems from data. Despite the wide occurrences of non-Gaussian fluctuations, the effective data-driven methods to identify stochastic differential equations with non-Gaussian L\'evy noise are relatively few so far. In this work, we propose a data-driven approach to extract stochastic governing laws with both (Gaussian) Brownian motion and (non-Gaussian) L\'evy motion, from short bursts of simulation data. Specifically, we use the normalizing flows technology to estimate the transition probability density function (solution of nonlocal Fokker-Planck equation) from data, and then substitute it into the recently proposed nonlocal Kramers-Moyal formulas to approximate L\'evy jump measure, drift coefficient and diffusion coefficient. We demonstrate that this approach can learn the stochastic differential equation with L\'evy motion. We present examples with one- and two-dimensional, decoupled and coupled systems to illustrate our method. This approach will become an effective tool for discovering stochastic governing laws and understanding complex dynamical behaviors.

Learning the temporal evolution of multivariate densities via normalizing flows

In this work, we propose a method to learn probability distributions using sample path data from stochastic differential equations. Specifically, we consider temporally evolving probability distributions (e.g., those produced by integrating local or nonlocal Fokker-Planck equations). We analyze this evolution through machine learning assisted construction of a time-dependent mapping that takes a reference distribution (say, a Gaussian) to each and every instance of our evolving distribution. If the reference distribution is the initial condition of a Fokker-Planck equation, what we learn is the time-T map of the corresponding solution. Specifically, the learned map is a normalizing flow that deforms the support of the reference density to the support of each and every density snapshot in time. We demonstrate that this approach can learn solutions to non-local Fokker-Planck equations, such as those arising in systems driven by both Brownian and L\'evy noise. We present examples with two- and three-dimensional, uni- and multimodal distributions to validate the method.