An evolutionary approach for discovering non-Gaussian stochastic dynamical systems based on nonlocal Kramers-Moyal formulas

Discovering explicit governing equations of stochastic dynamical systems with both (Gaussian) Brownian noise and (non-Gaussian) L\'evy noise from data is chanllenging due to possible intricate functional forms and the inherent complexity of L\'evy motion. This present research endeavors to develop an evolutionary symbol sparse regression (ESSR) approach to extract non-Gaussian stochastic dynamical systems from sample path data, based on nonlocal Kramers-Moyal formulas, genetic programming, and sparse regression. More specifically, the genetic programming is employed to generate a diverse array of candidate functions, the sparse regression technique aims at learning the coefficients associated with these candidates, and the nonlocal Kramers-Moyal formulas serve as the foundation for constructing the fitness measure in genetic programming and the loss function in sparse regression. The efficacy and capabilities of this approach are showcased through its application to several illustrative models. This approach stands out as a potent instrument for deciphering non-Gaussian stochastic dynamics from available datasets, indicating a wide range of applications across different fields.

CtrSVDD: A Benchmark Dataset and Baseline Analysis for Controlled Singing Voice Deepfake Detection

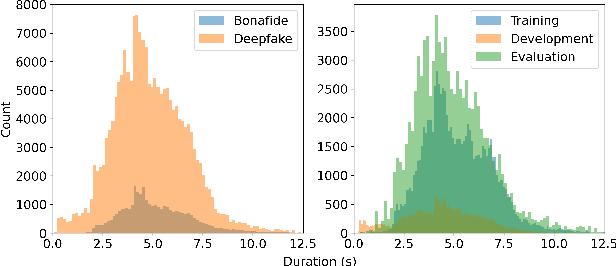
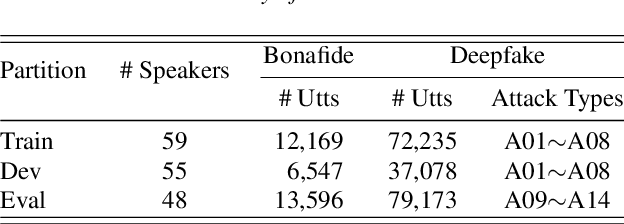
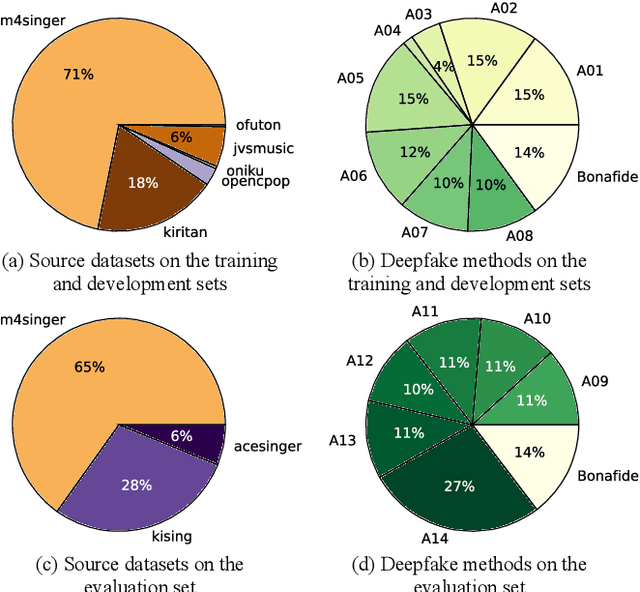
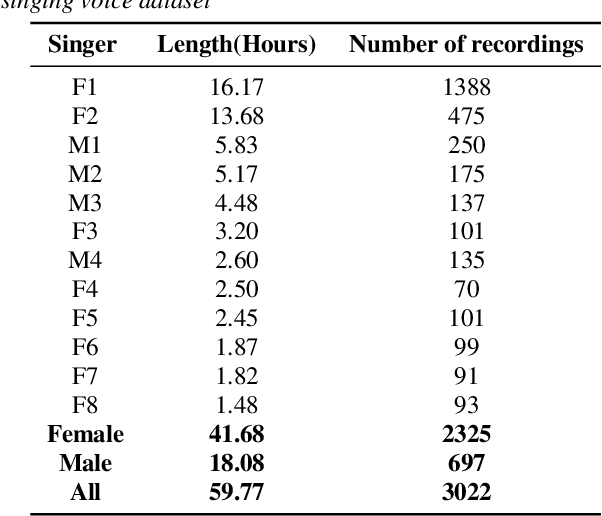
Recent singing voice synthesis and conversion advancements necessitate robust singing voice deepfake detection (SVDD) models. Current SVDD datasets face challenges due to limited controllability, diversity in deepfake methods, and licensing restrictions. Addressing these gaps, we introduce CtrSVDD, a large-scale, diverse collection of bonafide and deepfake singing vocals. These vocals are synthesized using state-of-the-art methods from publicly accessible singing voice datasets. CtrSVDD includes 47.64 hours of bonafide and 260.34 hours of deepfake singing vocals, spanning 14 deepfake methods and involving 164 singer identities. We also present a baseline system with flexible front-end features, evaluated against a structured train/dev/eval split. The experiments show the importance of feature selection and highlight a need for generalization towards deepfake methods that deviate further from training distribution. The CtrSVDD dataset and baselines are publicly accessible.

Controlling mean exit time of stochastic dynamical systems based on quasipotential and machine learning

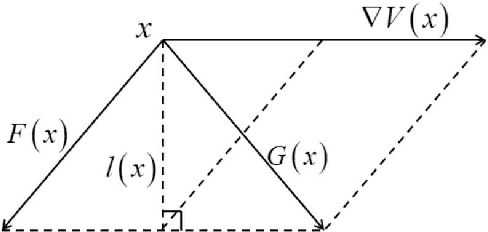
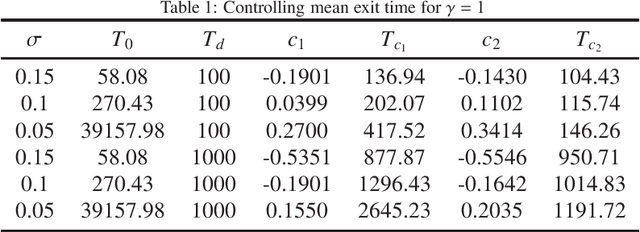
The mean exit time escaping basin of attraction in the presence of white noise is of practical importance in various scientific fields. In this work, we propose a strategy to control mean exit time of general stochastic dynamical systems to achieve a desired value based on the quasipotential concept and machine learning. Specifically, we develop a neural network architecture to compute the global quasipotential function. Then we design a systematic iterated numerical algorithm to calculate the controller for a given mean exit time. Moreover, we identify the most probable path between metastable attractors with help of the effective Hamilton-Jacobi scheme and the trained neural network. Numerical experiments demonstrate that our control strategy is effective and sufficiently accurate.

Human Mobility Prediction with Causal and Spatial-constrained Multi-task Network

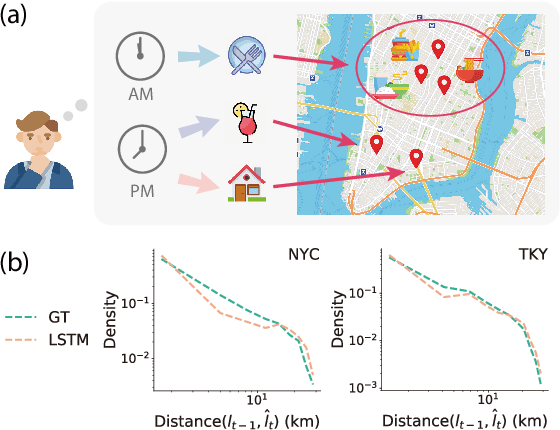
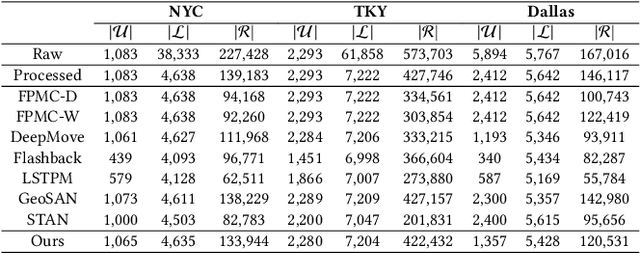
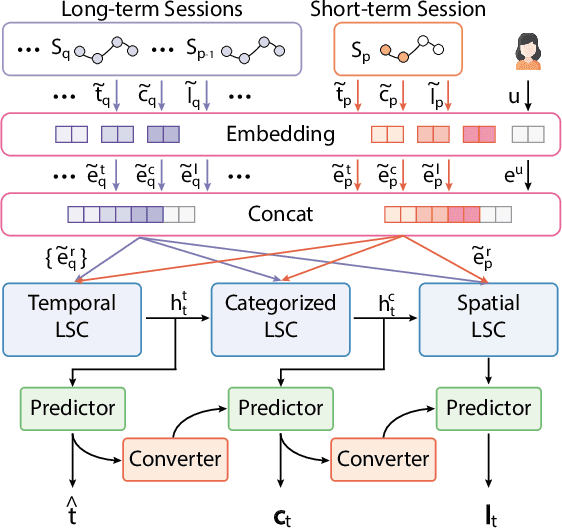
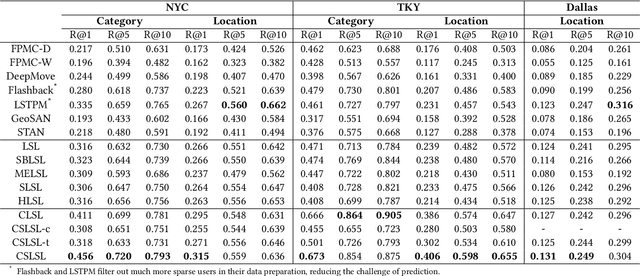
Modeling human mobility helps to understand how people are accessing resources and physically contacting with each other in cities, and thus contributes to various applications such as urban planning, epidemic control, and location-based advertisement. Next location prediction is one decisive task in individual human mobility modeling and is usually viewed as sequence modeling, solved with Markov or RNN-based methods. However, the existing models paid little attention to the logic of individual travel decisions and the reproducibility of the collective behavior of population. To this end, we propose a Causal and Spatial-constrained Long and Short-term Learner (CSLSL) for next location prediction. CSLSL utilizes a causal structure based on multi-task learning to explicitly model the "when$\rightarrow$what$\rightarrow$where", a.k.a. "time$\rightarrow$activity$\rightarrow$location" decision logic. We next propose a spatial-constrained loss function as an auxiliary task, to ensure the consistency between the predicted and actual spatial distribution of travelers' destinations. Moreover, CSLSL adopts modules named Long and Short-term Capturer (LSC) to learn the transition regularities across different time spans. Extensive experiments on three real-world datasets show a 33.4% performance improvement of CSLSL over baselines and confirm the effectiveness of introducing the causality and consistency constraints. The implementation is available at https://github.com/urbanmobility/CSLSL.

RefineGAN: Universally Generating Waveform Better than Ground Truth with Highly Accurate Pitch and Intensity Responses

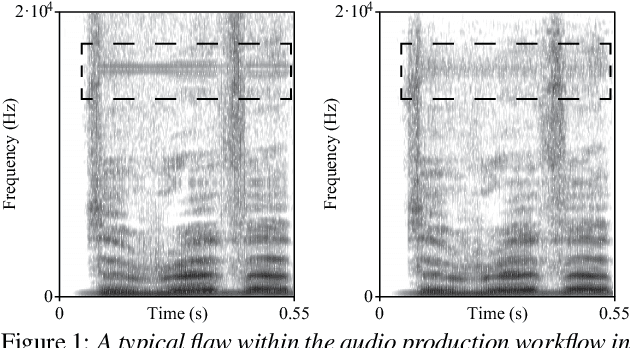
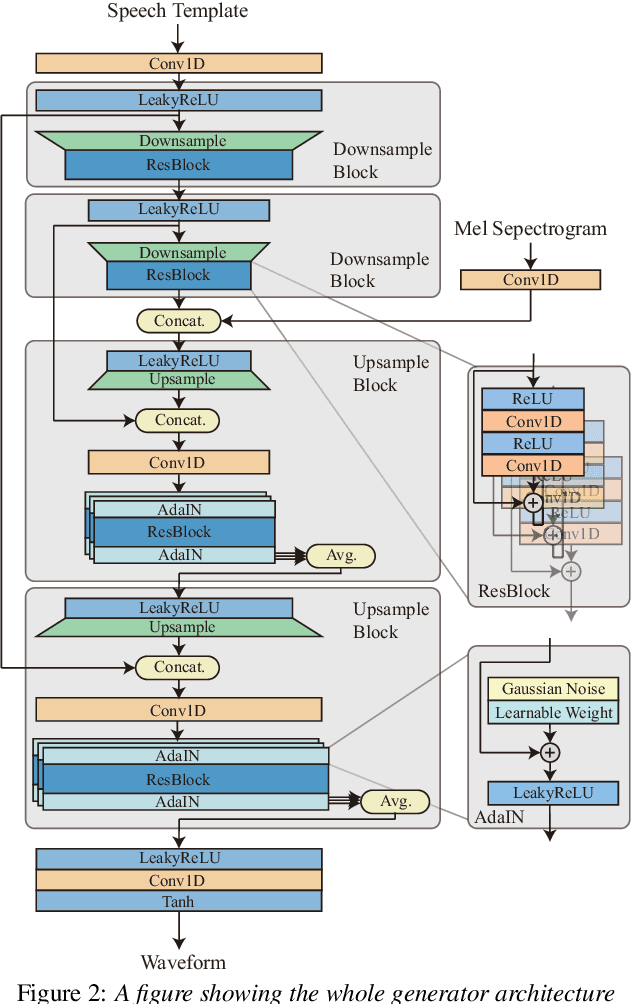
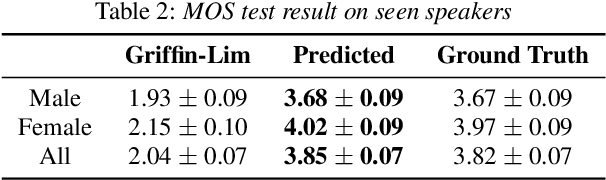
Most GAN(Generative Adversarial Network)-based approaches towards high-fidelity waveform generation heavily rely on discriminators to improve their performance. However, the over-use of this GAN method introduces much uncertainty into the generation process and often result in mismatches of pitch and intensity, which is fatal when it comes to sensitive using cases such as singing voice synthesis(SVS). To address this problem, we propose RefineGAN, a high-fidelity neural vocoder with faster-than-real-time generation capability, and focused on the robustness, pitch and intensity accuracy, and full-band audio generation. We employed a pitch-guided refine architecture with a multi-scale spectrogram-based loss function to help stabilize the training process and maintain the robustness of the neural vocoder while using the GAN-based training method. Audio generated using this method shows a better performance in subjective tests when compared with the ground-truth audio. This result shows that the fidelity is even improved during the waveform reconstruction by eliminating defects produced by the speaker and the recording procedure. Moreover, a further study shows that models trained on a specified type of data can perform on totally unseen language and unseen speaker identically well. Generated sample pairs are provided on https://timedomain-tech.github.io/refinegan/.

Extracting stochastic dynamical systems with $α$-stable Lévy noise from data

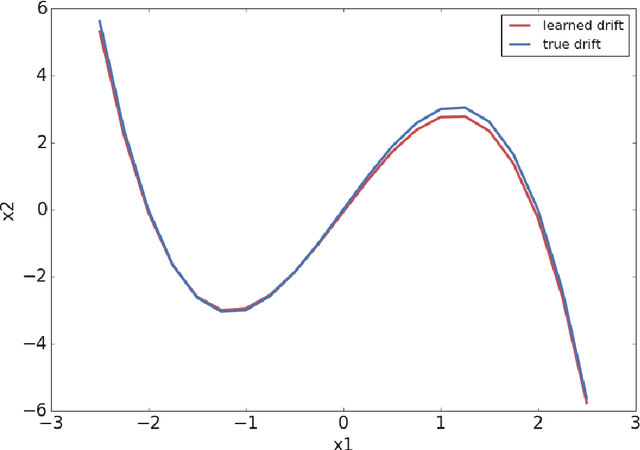
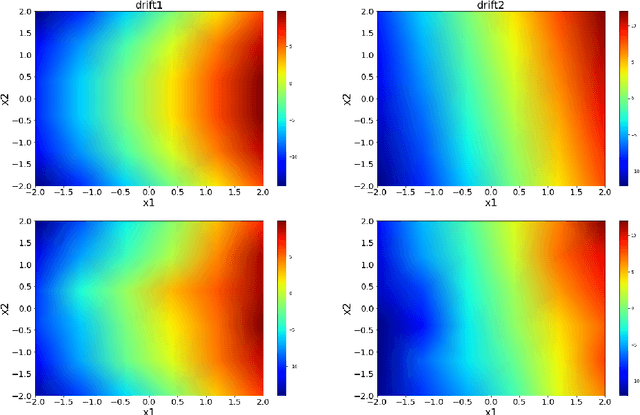
With the rapid increase of valuable observational, experimental and simulated data for complex systems, much efforts have been devoted to identifying governing laws underlying the evolution of these systems. Despite the wide applications of non-Gaussian fluctuations in numerous physical phenomena, the data-driven approaches to extract stochastic dynamical systems with (non-Gaussian) L\'evy noise are relatively few so far. In this work, we propose a data-driven method to extract stochastic dynamical systems with $\alpha$-stable L\'evy noise from short burst data based on the properties of $\alpha$-stable distributions. More specifically, we first estimate the L\'evy jump measure and noise intensity via computing mean and variance of the amplitude of the increment of the sample paths. Then we approximate the drift coefficient by combining nonlocal Kramers-Moyal formulas with normalizing flows. Numerical experiments on one- and two-dimensional prototypical examples illustrate the accuracy and effectiveness of our method. This approach will become an effective scientific tool in discovering stochastic governing laws of complex phenomena and understanding dynamical behaviors under non-Gaussian fluctuations.