Computing large deviation prefactors of stochastic dynamical systems based on machine learning

In this paper, we present large deviation theory that characterizes the exponential estimate for rare events of stochastic dynamical systems in the limit of weak noise. We aim to consider next-to-leading-order approximation for more accurate calculation of mean exit time via computing large deviation prefactors with the research efforts of machine learning. More specifically, we design a neural network framework to compute quasipotential, most probable paths and prefactors based on the orthogonal decomposition of vector field. We corroborate the higher effectiveness and accuracy of our algorithm with a practical example. Numerical experiments demonstrate its powerful function in exploring internal mechanism of rare events triggered by weak random fluctuations.

Controlling mean exit time of stochastic dynamical systems based on quasipotential and machine learning

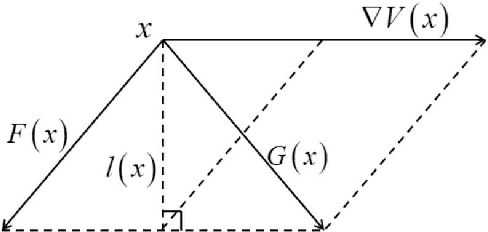
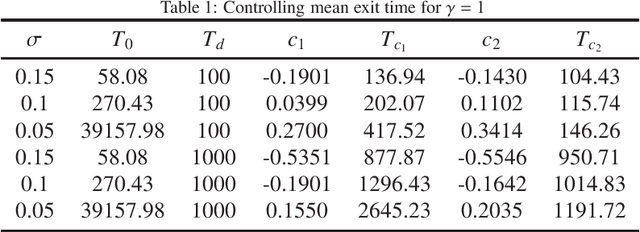
The mean exit time escaping basin of attraction in the presence of white noise is of practical importance in various scientific fields. In this work, we propose a strategy to control mean exit time of general stochastic dynamical systems to achieve a desired value based on the quasipotential concept and machine learning. Specifically, we develop a neural network architecture to compute the global quasipotential function. Then we design a systematic iterated numerical algorithm to calculate the controller for a given mean exit time. Moreover, we identify the most probable path between metastable attractors with help of the effective Hamilton-Jacobi scheme and the trained neural network. Numerical experiments demonstrate that our control strategy is effective and sufficiently accurate.