Learning Chemical Reaction Representation with Reactant-Product Alignment

Organic synthesis stands as a cornerstone of chemical industry. The development of robust machine learning models to support tasks associated with organic reactions is of significant interest. However, current methods rely on hand-crafted features or direct adaptations of model architectures from other domains, which lacks feasibility as data scales increase or overlook the rich chemical information inherent in reactions. To address these issues, this paper introduces {\modelname}, a novel chemical reaction representation learning model tailored for a variety of organic-reaction-related tasks. By integrating atomic correspondence between reactants and products, our model discerns the molecular transformations that occur during the reaction, thereby enhancing the comprehension of the reaction mechanism. We have designed an adapter structure to incorporate reaction conditions into the chemical reaction representation, allowing the model to handle diverse reaction conditions and adapt to various datasets and downstream tasks, e.g., reaction performance prediction. Additionally, we introduce a reaction-center aware attention mechanism that enables the model to concentrate on key functional groups, thereby generating potent representations for chemical reactions. Our model has been evaluated on a range of downstream tasks, including reaction condition prediction, reaction yield prediction, and reaction selectivity prediction. Experimental results indicate that our model markedly outperforms existing chemical reaction representation learning architectures across all tasks. Notably, our model significantly outperforms all the baselines with up to 25\% (top-1) and 16\% (top-10) increased accuracy over the strongest baseline on USPTO\_CONDITION dataset for reaction condition prediction. We plan to open-source the code contingent upon the acceptance of the paper.

Computing large deviation prefactors of stochastic dynamical systems based on machine learning

In this paper, we present large deviation theory that characterizes the exponential estimate for rare events of stochastic dynamical systems in the limit of weak noise. We aim to consider next-to-leading-order approximation for more accurate calculation of mean exit time via computing large deviation prefactors with the research efforts of machine learning. More specifically, we design a neural network framework to compute quasipotential, most probable paths and prefactors based on the orthogonal decomposition of vector field. We corroborate the higher effectiveness and accuracy of our algorithm with a practical example. Numerical experiments demonstrate its powerful function in exploring internal mechanism of rare events triggered by weak random fluctuations.

The Multi-Modal Video Reasoning and Analyzing Competition

In this paper, we introduce the Multi-Modal Video Reasoning and Analyzing Competition (MMVRAC) workshop in conjunction with ICCV 2021. This competition is composed of four different tracks, namely, video question answering, skeleton-based action recognition, fisheye video-based action recognition, and person re-identification, which are based on two datasets: SUTD-TrafficQA and UAV-Human. We summarize the top-performing methods submitted by the participants in this competition and show their results achieved in the competition.

A Machine Learning Framework for Computing the Most Probable Paths of Stochastic Dynamical Systems

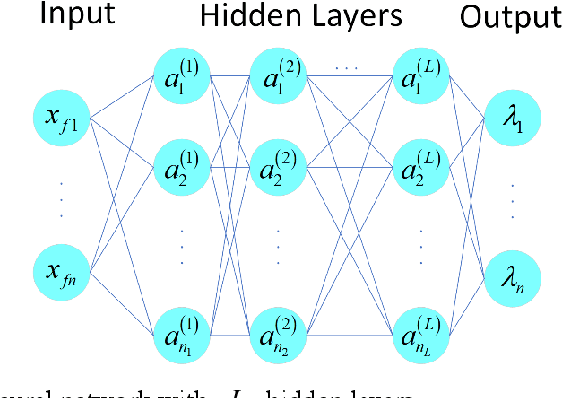
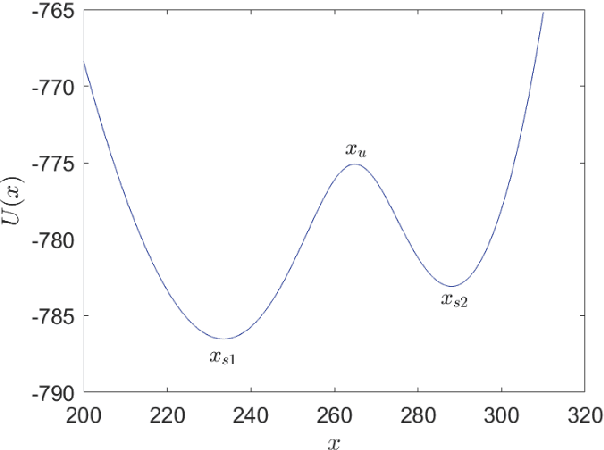
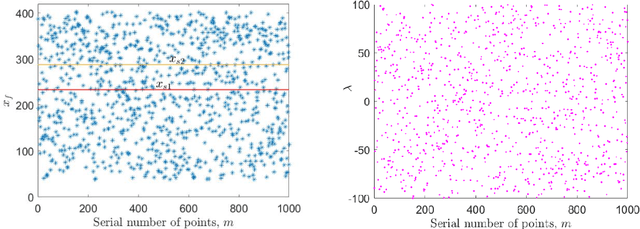
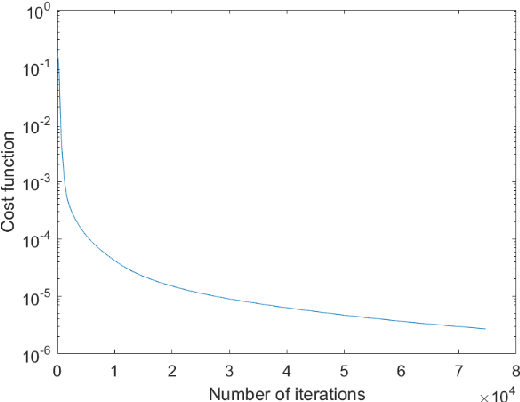
The emergence of transition phenomena between metastable states induced by noise plays a fundamental role in a broad range of nonlinear systems. The computation of the most probable paths is a key issue to understand the mechanism of transition behaviors. Shooting method is a common technique for this purpose, while losing its efficacy in high-dimensional systems. In the present work, we develop a machine learning framework to compute the most probable paths in the sense of Onsager-Machlup theory. Specifically, we reformulate the boundary value problem of Hamiltonian system and design a neural network to remedy the shortcomings of shooting method. The successful applications of our algorithms to several prototypical examples demonstrate its efficacy and accuracy for stochastic systems with both (Gaussian) Brownian noise and (non-Gaussian) L\'evy noise. This novel approach is effective in exploring the internal mechanisms of rare events triggered by random fluctuations in various scientific fields.