An evolutionary approach for discovering non-Gaussian stochastic dynamical systems based on nonlocal Kramers-Moyal formulas

Discovering explicit governing equations of stochastic dynamical systems with both (Gaussian) Brownian noise and (non-Gaussian) L\'evy noise from data is chanllenging due to possible intricate functional forms and the inherent complexity of L\'evy motion. This present research endeavors to develop an evolutionary symbol sparse regression (ESSR) approach to extract non-Gaussian stochastic dynamical systems from sample path data, based on nonlocal Kramers-Moyal formulas, genetic programming, and sparse regression. More specifically, the genetic programming is employed to generate a diverse array of candidate functions, the sparse regression technique aims at learning the coefficients associated with these candidates, and the nonlocal Kramers-Moyal formulas serve as the foundation for constructing the fitness measure in genetic programming and the loss function in sparse regression. The efficacy and capabilities of this approach are showcased through its application to several illustrative models. This approach stands out as a potent instrument for deciphering non-Gaussian stochastic dynamics from available datasets, indicating a wide range of applications across different fields.

Stochastic parameter reduced-order model based on hybrid machine learning approaches

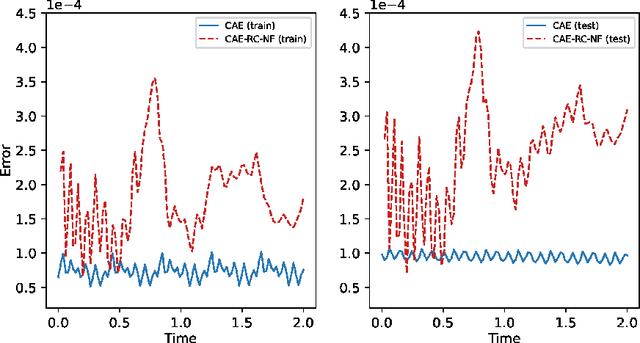
Establishing appropriate mathematical models for complex systems in natural phenomena not only helps deepen our understanding of nature but can also be used for state estimation and prediction. However, the extreme complexity of natural phenomena makes it extremely challenging to develop full-order models (FOMs) and apply them to studying many quantities of interest. In contrast, appropriate reduced-order models (ROMs) are favored due to their high computational efficiency and ability to describe the key dynamics and statistical characteristics of natural phenomena. Taking the viscous Burgers equation as an example, this paper constructs a Convolutional Autoencoder-Reservoir Computing-Normalizing Flow algorithm framework, where the Convolutional Autoencoder is used to construct latent space representations, and the Reservoir Computing-Normalizing Flow framework is used to characterize the evolution of latent state variables. In this way, a data-driven stochastic parameter reduced-order model is constructed to describe the complex system and its dynamic behavior.

Diffusion Model Conditioning on Gaussian Mixture Model and Negative Gaussian Mixture Gradient

Diffusion models (DMs) are a type of generative model that has a huge impact on image synthesis and beyond. They achieve state-of-the-art generation results in various generative tasks. A great diversity of conditioning inputs, such as text or bounding boxes, are accessible to control the generation. In this work, we propose a conditioning mechanism utilizing Gaussian mixture models (GMMs) as feature conditioning to guide the denoising process. Based on set theory, we provide a comprehensive theoretical analysis that shows that conditional latent distribution based on features and classes is significantly different, so that conditional latent distribution on features produces fewer defect generations than conditioning on classes. Two diffusion models conditioned on the Gaussian mixture model are trained separately for comparison. Experiments support our findings. A novel gradient function called the negative Gaussian mixture gradient (NGMG) is proposed and applied in diffusion model training with an additional classifier. Training stability has improved. We also theoretically prove that NGMG shares the same benefit as the Earth Mover distance (Wasserstein) as a more sensible cost function when learning distributions supported by low-dimensional manifolds.

Early Warning via tipping-preserving latent stochastic dynamical system and meta label correcting

Early warning for epilepsy patients is crucial for their safety and well-being, in terms of preventing or minimizing the severity of seizures. Through the patients' EEG data, we propose a meta learning framework for improving prediction on early ictal signals. To better utilize the meta label corrector method, we fuse the information from both the real data and the augmented data from the latent Stochastic differential equation(SDE). Besides, we also optimally select the latent dynamical system via distribution of transition time between real data and that from the latent SDE. In this way, the extracted tipping dynamical feature is also integrated into the meta network to better label the noisy data. To validate our method, LSTM is implemented as the baseline model. We conduct a series of experiments to predict seizure in various long-term window from 1-2 seconds input data and find surprisingly increment of prediction accuracy.

Early warning via transitions in latent stochastic dynamical systems

Early warnings for dynamical transitions in complex systems or high-dimensional observation data are essential in many real world applications, such as gene mutation, brain diseases, natural disasters, financial crises, and engineering reliability. To effectively extract early warning signals, we develop a novel approach: the directed anisotropic diffusion map that captures the latent evolutionary dynamics in low-dimensional manifold. Applying the methodology to authentic electroencephalogram (EEG) data, we successfully find the appropriate effective coordinates, and derive early warning signals capable of detecting the tipping point during the state transition. Our method bridges the latent dynamics with the original dataset. The framework is validated to be accurate and effective through numerical experiments, in terms of density and transition probability. It is shown that the second coordinate holds meaningful information for critical transition in various evaluation metrics.

Learning Stochastic Dynamical Systems as an Implicit Regularization with Graph Neural Networks

Stochastic Gumbel graph networks are proposed to learn high-dimensional time series, where the observed dimensions are often spatially correlated. To that end, the observed randomness and spatial-correlations are captured by learning the drift and diffusion terms of the stochastic differential equation with a Gumble matrix embedding, respectively. In particular, this novel framework enables us to investigate the implicit regularization effect of the noise terms in S-GGNs. We provide a theoretical guarantee for the proposed S-GGNs by deriving the difference between the two corresponding loss functions in a small neighborhood of weight. Then, we employ Kuramoto's model to generate data for comparing the spectral density from the Hessian Matrix of the two loss functions. Experimental results on real-world data, demonstrate that S-GGNs exhibit superior convergence, robustness, and generalization, compared with state-of-the-arts.

Reservoir Computing with Error Correction: Long-term Behaviors of Stochastic Dynamical Systems

The prediction of stochastic dynamical systems and the capture of dynamical behaviors are profound problems. In this article, we propose a data-driven framework combining Reservoir Computing and Normalizing Flow to study this issue, which mimics error modeling to improve the traditional Reservoir Computing performance and takes advantage of both approaches. This model-free method successfully predicts the long-term evolution of stochastic dynamical systems and replicates dynamical behaviors. With few assumptions about the underlying stochastic dynamical systems, we deal with Markov/non-Markov and stationary/non-stationary stochastic processes defined by linear/nonlinear stochastic differential equations or stochastic delay differential equations. We verify the effectiveness of the proposed framework in five experiments, including the Ornstein-Uhlenbeck process, Double-Well system, El Ni\~no Southern Oscillation simplified model, and stochastic Lorenz system. Additionally, we explore the noise-induced tipping phenomena and the replication of the strange attractor.

Meta contrastive label correction for financial time series

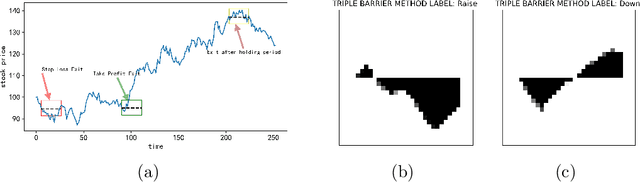
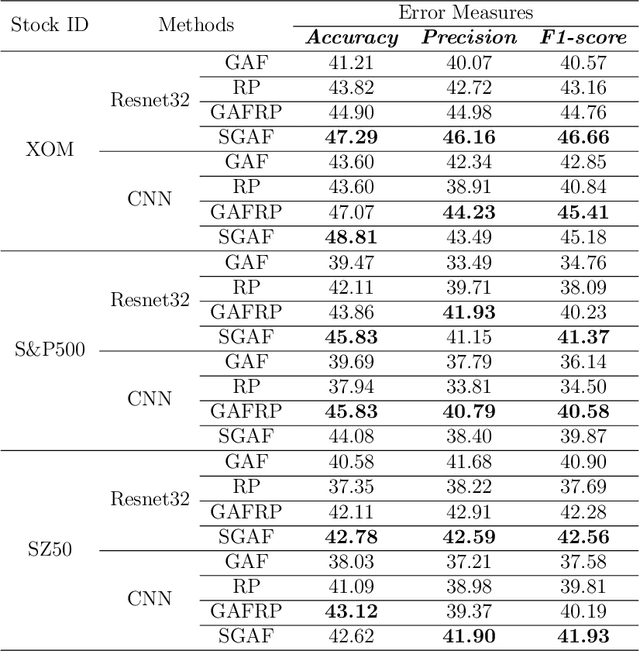
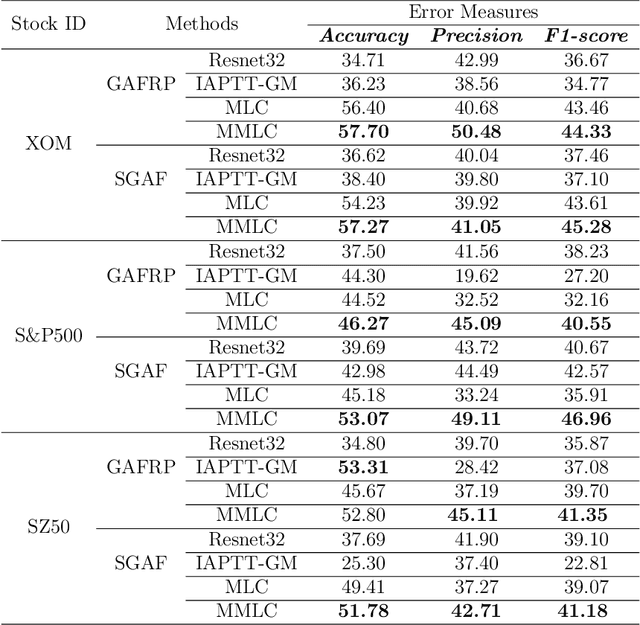
Financial applications such as stock price forecasting, usually face an issue that under the predefined labeling rules, it is hard to accurately predict the directions of stock movement. This is because traditional ways of labeling, taking Triple Barrier Method, for example, usually gives us inaccurate or even corrupted labels. To address this issue, we focus on two main goals. One is that our proposed method can automatically generate correct labels for noisy time series patterns, while at the same time, the method is capable of boosting classification performance on this new labeled dataset. Based on the aforementioned goals, our approach has the following three novelties: First, we fuse a new contrastive learning algorithm into the meta-learning framework to estimate correct labels iteratively when updating the classification model inside. Moreover, we utilize images generated from time series data through Gramian angular field and representative learning. Most important of all, we adopt multi-task learning to forecast temporal-variant labels. In the experiments, we work on 6% clean data and the rest unlabeled data. It is shown that our method is competitive and outperforms a lot compared with benchmarks.

Auto-SDE: Learning effective reduced dynamics from data-driven stochastic dynamical systems

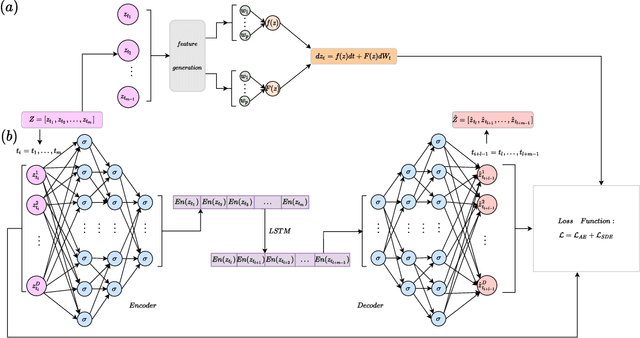
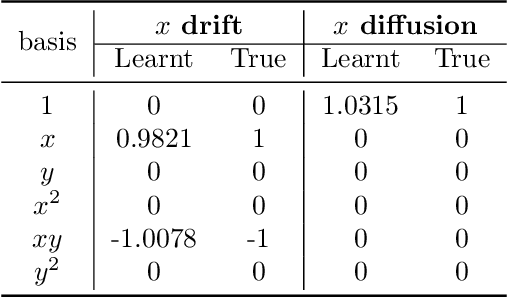
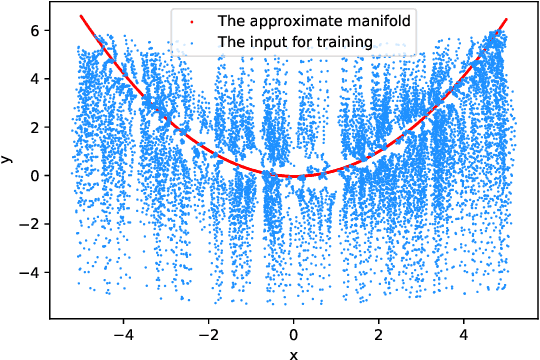
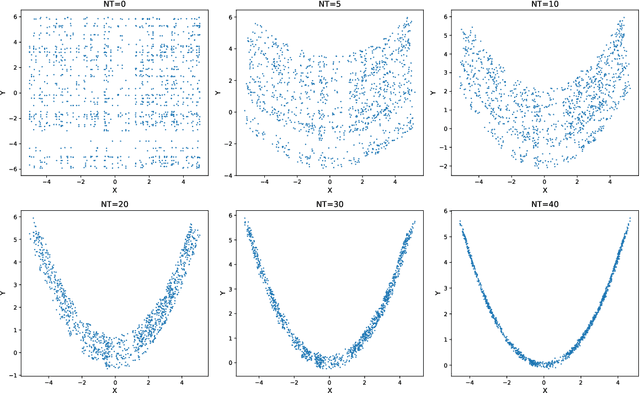
Multiscale stochastic dynamical systems have been widely adopted to scientific and engineering problems due to their capability of depicting complex phenomena in many real world applications. This work is devoted to investigating the effective reduced dynamics for a slow-fast stochastic dynamical system. Given observation data on a short-term period satisfying some unknown slow-fast stochastic system, we propose a novel algorithm including a neural network called Auto-SDE to learn invariant slow manifold. Our approach captures the evolutionary nature of a series of time-dependent autoencoder neural networks with the loss constructed from a discretized stochastic differential equation. Our algorithm is also proved to be accurate, stable and effective through numerical experiments under various evaluation metrics.

An Optimal Control Method to Compute the Most Likely Transition Path for Stochastic Dynamical Systems with Jumps

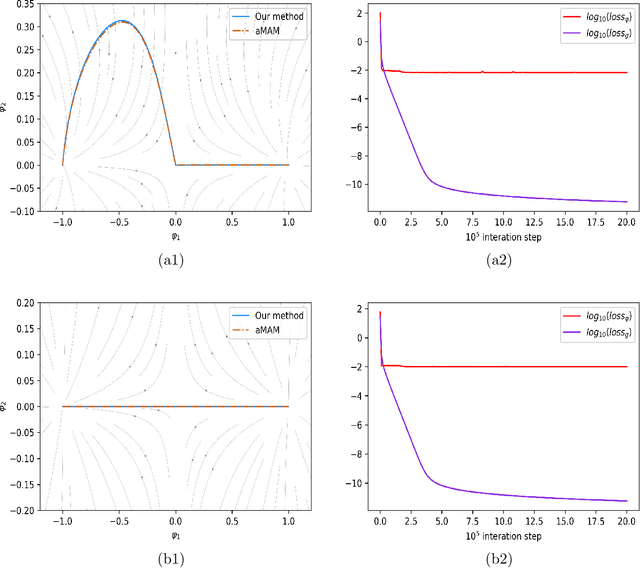
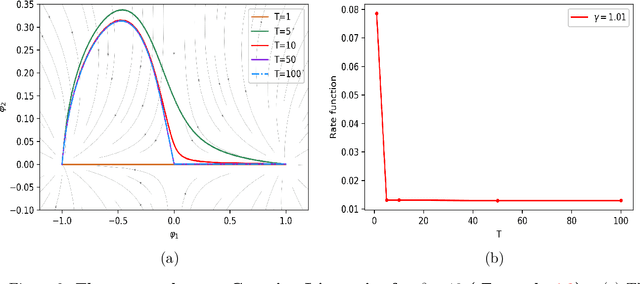
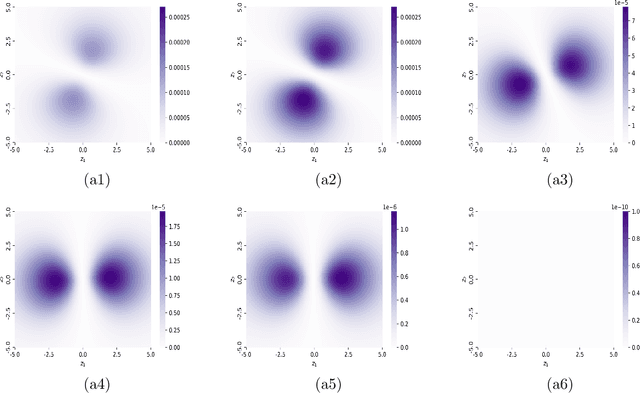
Many complex real world phenomena exhibit abrupt, intermittent or jumping behaviors, which are more suitable to be described by stochastic differential equations under non-Gaussian L\'evy noise. Among these complex phenomena, the most likely transition paths between metastable states are important since these rare events may have high impact in certain scenarios. Based on the large deviation principle, the most likely transition path could be treated as the minimizer of the rate function upon paths that connect two points. One of the challenges to calculate the most likely transition path for stochastic dynamical systems under non-Gaussian L\'evy noise is that the associated rate function can not be explicitly expressed by paths. For this reason, we formulate an optimal control problem to obtain the optimal state as the most likely transition path. We then develop a neural network method to solve this issue. Several experiments are investigated for both Gaussian and non-Gaussian cases.