Hierarchical-Graph-Structured Edge Partition Models for Learning Evolving Community Structure

We propose a novel dynamic network model to capture evolving latent communities within temporal networks. To achieve this, we decompose each observed dynamic edge between vertices using a Poisson-gamma edge partition model, assigning each vertex to one or more latent communities through \emph{nonnegative} vertex-community memberships. Specifically, hierarchical transition kernels are employed to model the interactions between these latent communities in the observed temporal network. A hierarchical graph prior is placed on the transition structure of the latent communities, allowing us to model how they evolve and interact over time. Consequently, our dynamic network enables the inferred community structure to merge, split, and interact with one another, providing a comprehensive understanding of complex network dynamics. Experiments on various real-world network datasets demonstrate that the proposed model not only effectively uncovers interpretable latent structures but also surpasses other state-of-the art dynamic network models in the tasks of link prediction and community detection.

On Your Mark, Get Set, Predict! Modeling Continuous-Time Dynamics of Cascades for Information Popularity Prediction

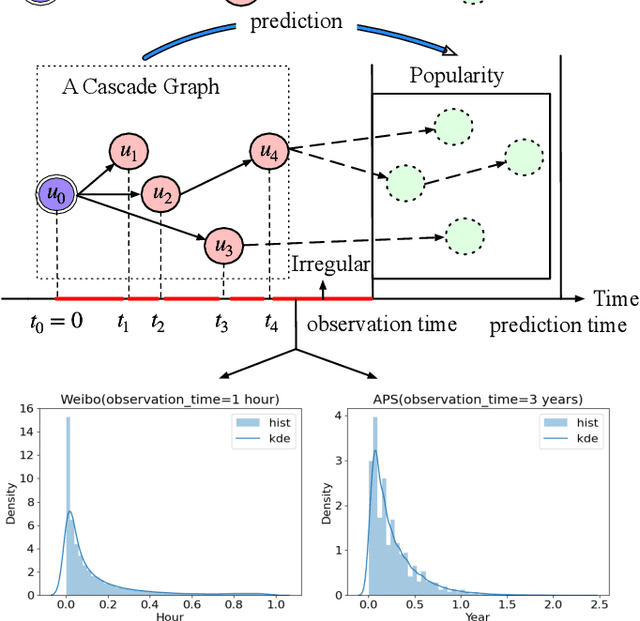
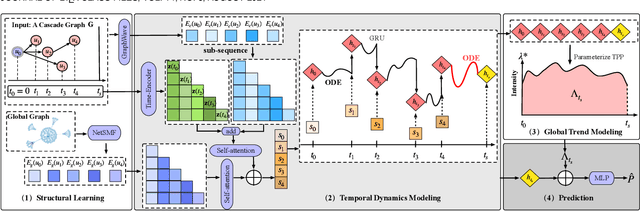
Information popularity prediction is important yet challenging in various domains, including viral marketing and news recommendations. The key to accurately predicting information popularity lies in subtly modeling the underlying temporal information diffusion process behind observed events of an information cascade, such as the retweets of a tweet. To this end, most existing methods either adopt recurrent networks to capture the temporal dynamics from the first to the last observed event or develop a statistical model based on self-exciting point processes to make predictions. However, information diffusion is intrinsically a complex continuous-time process with irregularly observed discrete events, which is oversimplified using recurrent networks as they fail to capture the irregular time intervals between events, or using self-exciting point processes as they lack flexibility to capture the complex diffusion process. Against this background, we propose ConCat, modeling the Continuous-time dynamics of Cascades for information popularity prediction. On the one hand, it leverages neural Ordinary Differential Equations (ODEs) to model irregular events of a cascade in continuous time based on the cascade graph and sequential event information. On the other hand, it considers cascade events as neural temporal point processes (TPPs) parameterized by a conditional intensity function which can also benefit the popularity prediction task. We conduct extensive experiments to evaluate ConCat on three real-world datasets. Results show that ConCat achieves superior performance compared to state-of-the-art baselines, yielding a 2.3%-33.2% improvement over the best-performing baselines across the three datasets.

Negative-Binomial Randomized Gamma Markov Processes for Heterogeneous Overdispersed Count Time Series

Modeling count-valued time series has been receiving increasing attention since count time series naturally arise in physical and social domains. Poisson gamma dynamical systems (PGDSs) are newly-developed methods, which can well capture the expressive latent transition structure and bursty dynamics behind count sequences. In particular, PGDSs demonstrate superior performance in terms of data imputation and prediction, compared with canonical linear dynamical system (LDS) based methods. Despite these advantages, PGDS cannot capture the heterogeneous overdispersed behaviours of the underlying dynamic processes. To mitigate this defect, we propose a negative-binomial-randomized gamma Markov process, which not only significantly improves the predictive performance of the proposed dynamical system, but also facilitates the fast convergence of the inference algorithm. Moreover, we develop methods to estimate both factor-structured and graph-structured transition dynamics, which enable us to infer more explainable latent structure, compared with PGDSs. Finally, we demonstrate the explainable latent structure learned by the proposed method, and show its superior performance in imputing missing data and forecasting future observations, compared with the related models.

Scaling up Dynamic Edge Partition Models via Stochastic Gradient MCMC

The edge partition model (EPM) is a generative model for extracting an overlapping community structure from static graph-structured data. In the EPM, the gamma process (GaP) prior is adopted to infer the appropriate number of latent communities, and each vertex is endowed with a gamma distributed positive memberships vector. Despite having many attractive properties, inference in the EPM is typically performed using Markov chain Monte Carlo (MCMC) methods that prevent it from being applied to massive network data. In this paper, we generalize the EPM to account for dynamic enviroment by representing each vertex with a positive memberships vector constructed using Dirichlet prior specification, and capturing the time-evolving behaviour of vertices via a Dirichlet Markov chain construction. A simple-to-implement Gibbs sampler is proposed to perform posterior computation using Negative- Binomial augmentation technique. For large network data, we propose a stochastic gradient Markov chain Monte Carlo (SG-MCMC) algorithm for scalable inference in the proposed model. The experimental results show that the novel methods achieve competitive performance in terms of link prediction, while being much faster.

Poisson-Gamma Dynamical Systems with Non-Stationary Transition Dynamics

Bayesian methodologies for handling count-valued time series have gained prominence due to their ability to infer interpretable latent structures and to estimate uncertainties, and thus are especially suitable for dealing with noisy and incomplete count data. Among these Bayesian models, Poisson-Gamma Dynamical Systems (PGDSs) are proven to be effective in capturing the evolving dynamics underlying observed count sequences. However, the state-of-the-art PGDS still falls short in capturing the time-varying transition dynamics that are commonly observed in real-world count time series. To mitigate this limitation, a non-stationary PGDS is proposed to allow the underlying transition matrices to evolve over time, and the evolving transition matrices are modeled by sophisticatedly-designed Dirichlet Markov chains. Leveraging Dirichlet-Multinomial-Beta data augmentation techniques, a fully-conjugate and efficient Gibbs sampler is developed to perform posterior simulation. Experiments show that, in comparison with related models, the proposed non-stationary PGDS achieves improved predictive performance due to its capacity to learn non-stationary dependency structure captured by the time-evolving transition matrices.

Dynamic Latent Graph-Guided Neural Temporal Point Processes

Continuously-observed event occurrences, often exhibit self- and mutually-exciting effects, which can be well modeled using temporal point processes. Beyond that, these event dynamics may also change over time, with certain periodic trends. We propose a novel variational auto-encoder to capture such a mixture of temporal dynamics. More specifically, the whole time interval of the input sequence is partitioned into a set of sub-intervals. The event dynamics are assumed to be stationary within each sub-interval, but could be changing across those sub-intervals. In particular, we use a sequential latent variable model to learn a dependency graph between the observed dimensions, for each sub-interval. The model predicts the future event times, by using the learned dependency graph to remove the noncontributing influences of past events. By doing so, the proposed model demonstrates its higher accuracy in predicting inter-event times and event types for several real-world event sequences, compared with existing state of the art neural point processes.

Learning Stochastic Dynamical Systems as an Implicit Regularization with Graph Neural Networks

Stochastic Gumbel graph networks are proposed to learn high-dimensional time series, where the observed dimensions are often spatially correlated. To that end, the observed randomness and spatial-correlations are captured by learning the drift and diffusion terms of the stochastic differential equation with a Gumble matrix embedding, respectively. In particular, this novel framework enables us to investigate the implicit regularization effect of the noise terms in S-GGNs. We provide a theoretical guarantee for the proposed S-GGNs by deriving the difference between the two corresponding loss functions in a small neighborhood of weight. Then, we employ Kuramoto's model to generate data for comparing the spectral density from the Hessian Matrix of the two loss functions. Experimental results on real-world data, demonstrate that S-GGNs exhibit superior convergence, robustness, and generalization, compared with state-of-the-arts.

Estimating Latent Population Flows from Aggregated Data via Inversing Multi-Marginal Optimal Transport

We study the problem of estimating latent population flows from aggregated count data. This problem arises when individual trajectories are not available due to privacy issues or measurement fidelity. Instead, the aggregated observations are measured over discrete-time points, for estimating the population flows among states. Most related studies tackle the problems by learning the transition parameters of a time-homogeneous Markov process. Nonetheless, most real-world population flows can be influenced by various uncertainties such as traffic jam and weather conditions. Thus, in many cases, a time-homogeneous Markov model is a poor approximation of the much more complex population flows. To circumvent this difficulty, we resort to a multi-marginal optimal transport (MOT) formulation that can naturally represent aggregated observations with constrained marginals, and encode time-dependent transition matrices by the cost functions. In particular, we propose to estimate the transition flows from aggregated data by learning the cost functions of the MOT framework, which enables us to capture time-varying dynamic patterns. The experiments demonstrate the improved accuracy of the proposed algorithms than the related methods in estimating several real-world transition flows.

Collapsed Variational Inference for Nonparametric Bayesian Group Factor Analysis

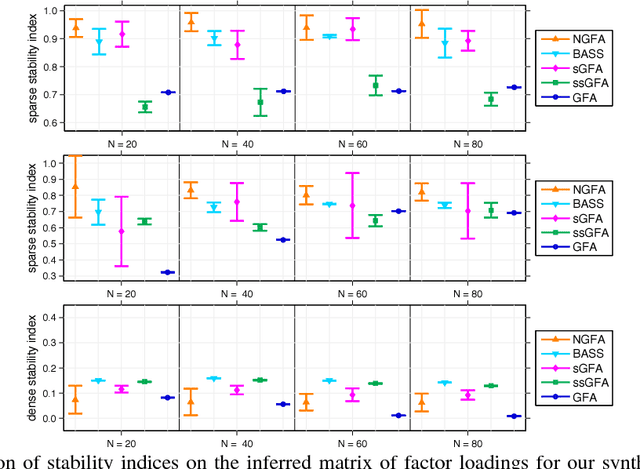
Group factor analysis (GFA) methods have been widely used to infer the common structure and the group-specific signals from multiple related datasets in various fields including systems biology and neuroimaging. To date, most available GFA models require Gibbs sampling or slice sampling to perform inference, which prevents the practical application of GFA to large-scale data. In this paper we present an efficient collapsed variational inference (CVI) algorithm for the nonparametric Bayesian group factor analysis (NGFA) model built upon an hierarchical beta Bernoulli process. Our CVI algorithm proceeds by marginalizing out the group-specific beta process parameters, and then approximating the true posterior in the collapsed space using mean field methods. Experimental results on both synthetic and real-world data demonstrate the effectiveness of our CVI algorithm for the NGFA compared with state-of-the-art GFA methods.