Zero-shot Robotic Manipulation with Language-guided Instruction and Formal Task Planning

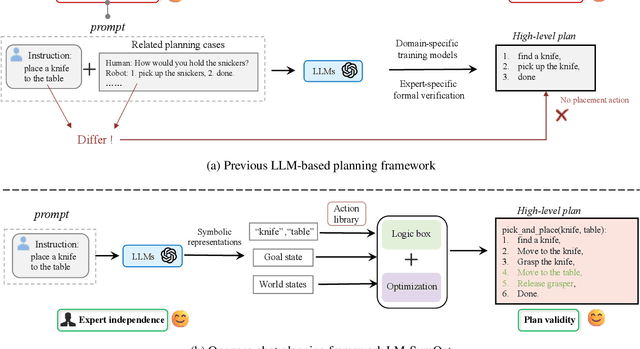
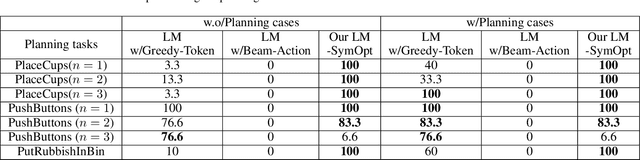
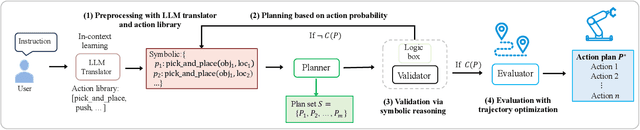
Robotic manipulation is often challenging due to the long-horizon tasks and the complex object relationships. A common solution is to develop a task and motion planning framework that integrates planning for high-level task and low-level motion. Recently, inspired by the powerful reasoning ability of Large Language Models (LLMs), LLM-based planning approaches have achieved remarkable progress. However, these methods still heavily rely on expert-specific knowledge, often generating invalid plans for unseen and unfamiliar tasks. To address this issue, we propose an innovative language-guided symbolic task planning (LM-SymOpt) framework with optimization. It is the first expert-free planning framework since we combine the world knowledge from LLMs with formal reasoning, resulting in improved generalization capability to new tasks. Specifically, differ to most existing work, our LM-SymOpt employs LLMs to translate natural language instructions into symbolic representations, thereby representing actions as high-level symbols and reducing the search space for planning. Next, after evaluating the action probability of completing the task using LLMs, a weighted random sampling method is introduced to generate candidate plans. Their feasibility is assessed through symbolic reasoning and their cost efficiency is then evaluated using trajectory optimization for selecting the optimal planning. Our experimental results show that LM-SymOpt outperforms existing LLM-based planning approaches.

Early Warning via tipping-preserving latent stochastic dynamical system and meta label correcting

Early warning for epilepsy patients is crucial for their safety and well-being, in terms of preventing or minimizing the severity of seizures. Through the patients' EEG data, we propose a meta learning framework for improving prediction on early ictal signals. To better utilize the meta label corrector method, we fuse the information from both the real data and the augmented data from the latent Stochastic differential equation(SDE). Besides, we also optimally select the latent dynamical system via distribution of transition time between real data and that from the latent SDE. In this way, the extracted tipping dynamical feature is also integrated into the meta network to better label the noisy data. To validate our method, LSTM is implemented as the baseline model. We conduct a series of experiments to predict seizure in various long-term window from 1-2 seconds input data and find surprisingly increment of prediction accuracy.

Early warning via transitions in latent stochastic dynamical systems

Early warnings for dynamical transitions in complex systems or high-dimensional observation data are essential in many real world applications, such as gene mutation, brain diseases, natural disasters, financial crises, and engineering reliability. To effectively extract early warning signals, we develop a novel approach: the directed anisotropic diffusion map that captures the latent evolutionary dynamics in low-dimensional manifold. Applying the methodology to authentic electroencephalogram (EEG) data, we successfully find the appropriate effective coordinates, and derive early warning signals capable of detecting the tipping point during the state transition. Our method bridges the latent dynamics with the original dataset. The framework is validated to be accurate and effective through numerical experiments, in terms of density and transition probability. It is shown that the second coordinate holds meaningful information for critical transition in various evaluation metrics.

Learning Stochastic Dynamical Systems as an Implicit Regularization with Graph Neural Networks

Stochastic Gumbel graph networks are proposed to learn high-dimensional time series, where the observed dimensions are often spatially correlated. To that end, the observed randomness and spatial-correlations are captured by learning the drift and diffusion terms of the stochastic differential equation with a Gumble matrix embedding, respectively. In particular, this novel framework enables us to investigate the implicit regularization effect of the noise terms in S-GGNs. We provide a theoretical guarantee for the proposed S-GGNs by deriving the difference between the two corresponding loss functions in a small neighborhood of weight. Then, we employ Kuramoto's model to generate data for comparing the spectral density from the Hessian Matrix of the two loss functions. Experimental results on real-world data, demonstrate that S-GGNs exhibit superior convergence, robustness, and generalization, compared with state-of-the-arts.

Reservoir Computing with Error Correction: Long-term Behaviors of Stochastic Dynamical Systems

The prediction of stochastic dynamical systems and the capture of dynamical behaviors are profound problems. In this article, we propose a data-driven framework combining Reservoir Computing and Normalizing Flow to study this issue, which mimics error modeling to improve the traditional Reservoir Computing performance and takes advantage of both approaches. This model-free method successfully predicts the long-term evolution of stochastic dynamical systems and replicates dynamical behaviors. With few assumptions about the underlying stochastic dynamical systems, we deal with Markov/non-Markov and stationary/non-stationary stochastic processes defined by linear/nonlinear stochastic differential equations or stochastic delay differential equations. We verify the effectiveness of the proposed framework in five experiments, including the Ornstein-Uhlenbeck process, Double-Well system, El Ni\~no Southern Oscillation simplified model, and stochastic Lorenz system. Additionally, we explore the noise-induced tipping phenomena and the replication of the strange attractor.

Meta contrastive label correction for financial time series

Financial applications such as stock price forecasting, usually face an issue that under the predefined labeling rules, it is hard to accurately predict the directions of stock movement. This is because traditional ways of labeling, taking Triple Barrier Method, for example, usually gives us inaccurate or even corrupted labels. To address this issue, we focus on two main goals. One is that our proposed method can automatically generate correct labels for noisy time series patterns, while at the same time, the method is capable of boosting classification performance on this new labeled dataset. Based on the aforementioned goals, our approach has the following three novelties: First, we fuse a new contrastive learning algorithm into the meta-learning framework to estimate correct labels iteratively when updating the classification model inside. Moreover, we utilize images generated from time series data through Gramian angular field and representative learning. Most important of all, we adopt multi-task learning to forecast temporal-variant labels. In the experiments, we work on 6% clean data and the rest unlabeled data. It is shown that our method is competitive and outperforms a lot compared with benchmarks.

GT-CausIn: a novel causal-based insight for traffic prediction

Traffic forecasting is an important application of spatiotemporal series prediction. Among different methods, graph neural networks have achieved so far the most promising results, learning relations between graph nodes then becomes a crucial task. However, improvement space is very limited when these relations are learned in a node-to-node manner. The challenge stems from (1) obscure temporal dependencies between different stations, (2) difficulties in defining variables beyond the node level, and (3) no ready-made method to validate the learned relations. To confront these challenges, we define legitimate traffic causal variables to discover the causal relation inside the traffic network, which is carefully checked with statistic tools and case analysis. We then present a novel model named Graph Spatial-Temporal Network Based on Causal Insight (GT-CausIn), where prior learned causal information is integrated with graph diffusion layers and temporal convolutional network (TCN) layers. Experiments are carried out on two real-world traffic datasets: PEMS-BAY and METR-LA, which show that GT-CausIn significantly outperforms the state-of-the-art models on mid-term and long-term prediction.

Stock Trading Optimization through Model-based Reinforcement Learning with Resistance Support Relative Strength

Reinforcement learning (RL) is gaining attention by more and more researchers in quantitative finance as the agent-environment interaction framework is aligned with decision making process in many business problems. Most of the current financial applications using RL algorithms are based on model-free method, which still faces stability and adaptivity challenges. As lots of cutting-edge model-based reinforcement learning (MBRL) algorithms mature in applications such as video games or robotics, we design a new approach that leverages resistance and support (RS) level as regularization terms for action in MBRL, to improve the algorithm's efficiency and stability. From the experiment results, we can see RS level, as a market timing technique, enhances the performance of pure MBRL models in terms of various measurements and obtains better profit gain with less riskiness. Besides, our proposed method even resists big drop (less maximum drawdown) during COVID-19 pandemic period when the financial market got unpredictable crisis. Explanations on why control of resistance and support level can boost MBRL is also investigated through numerical experiments, such as loss of actor-critic network and prediction error of the transition dynamical model. It shows that RS indicators indeed help the MBRL algorithms to converge faster at early stage and obtain smaller critic loss as training episodes increase.

Auto-SDE: Learning effective reduced dynamics from data-driven stochastic dynamical systems

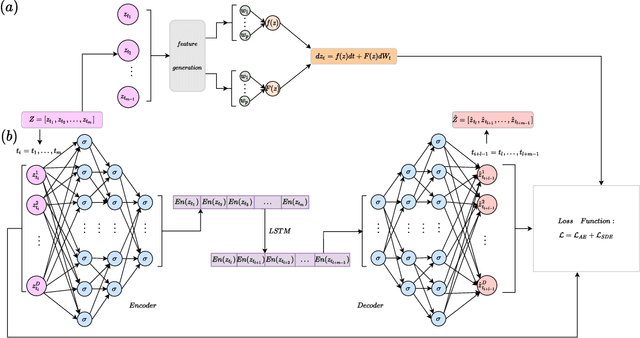
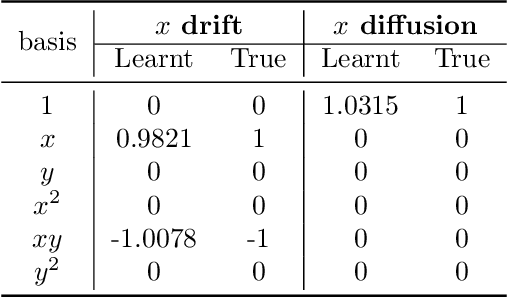
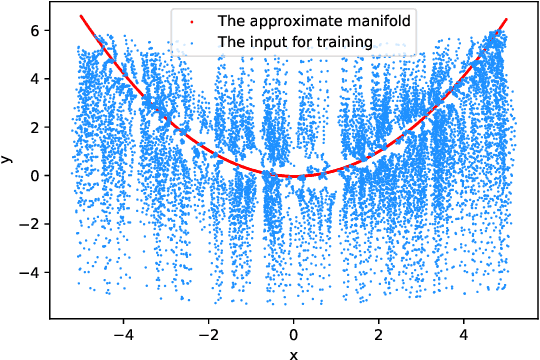
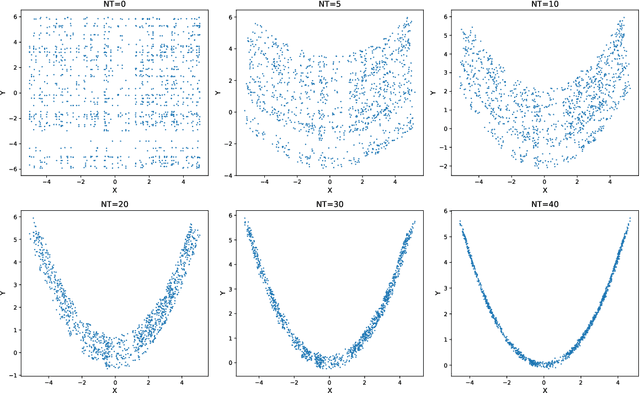
Multiscale stochastic dynamical systems have been widely adopted to scientific and engineering problems due to their capability of depicting complex phenomena in many real world applications. This work is devoted to investigating the effective reduced dynamics for a slow-fast stochastic dynamical system. Given observation data on a short-term period satisfying some unknown slow-fast stochastic system, we propose a novel algorithm including a neural network called Auto-SDE to learn invariant slow manifold. Our approach captures the evolutionary nature of a series of time-dependent autoencoder neural networks with the loss constructed from a discretized stochastic differential equation. Our algorithm is also proved to be accurate, stable and effective through numerical experiments under various evaluation metrics.

An Optimal Control Method to Compute the Most Likely Transition Path for Stochastic Dynamical Systems with Jumps

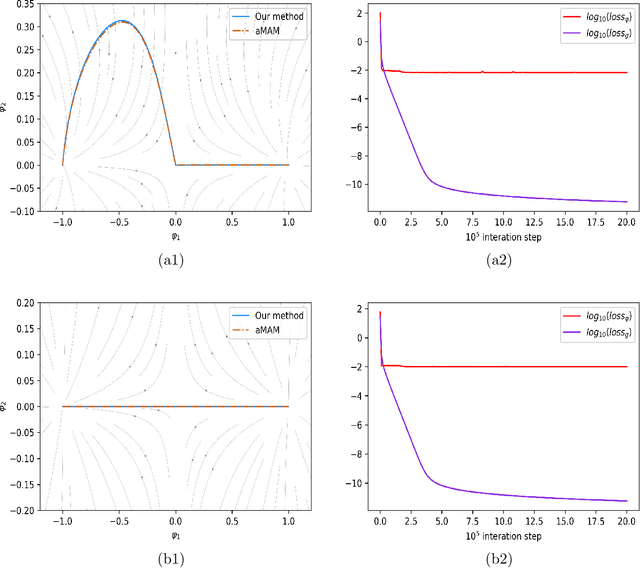
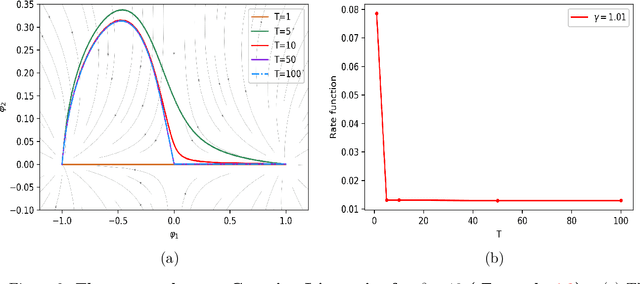
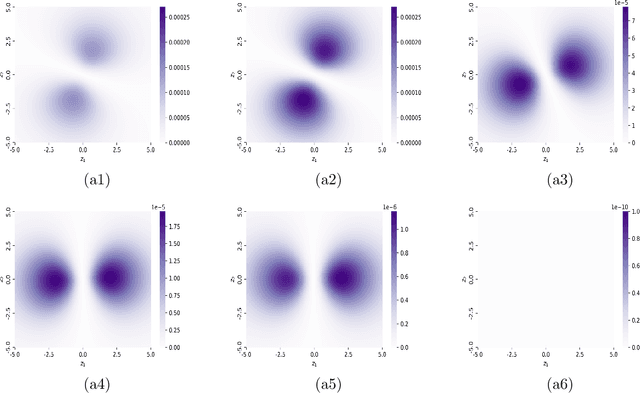
Many complex real world phenomena exhibit abrupt, intermittent or jumping behaviors, which are more suitable to be described by stochastic differential equations under non-Gaussian L\'evy noise. Among these complex phenomena, the most likely transition paths between metastable states are important since these rare events may have high impact in certain scenarios. Based on the large deviation principle, the most likely transition path could be treated as the minimizer of the rate function upon paths that connect two points. One of the challenges to calculate the most likely transition path for stochastic dynamical systems under non-Gaussian L\'evy noise is that the associated rate function can not be explicitly expressed by paths. For this reason, we formulate an optimal control problem to obtain the optimal state as the most likely transition path. We then develop a neural network method to solve this issue. Several experiments are investigated for both Gaussian and non-Gaussian cases.