Early warning via transitions in latent stochastic dynamical systems

Early warnings for dynamical transitions in complex systems or high-dimensional observation data are essential in many real world applications, such as gene mutation, brain diseases, natural disasters, financial crises, and engineering reliability. To effectively extract early warning signals, we develop a novel approach: the directed anisotropic diffusion map that captures the latent evolutionary dynamics in low-dimensional manifold. Applying the methodology to authentic electroencephalogram (EEG) data, we successfully find the appropriate effective coordinates, and derive early warning signals capable of detecting the tipping point during the state transition. Our method bridges the latent dynamics with the original dataset. The framework is validated to be accurate and effective through numerical experiments, in terms of density and transition probability. It is shown that the second coordinate holds meaningful information for critical transition in various evaluation metrics.

Auto-SDE: Learning effective reduced dynamics from data-driven stochastic dynamical systems

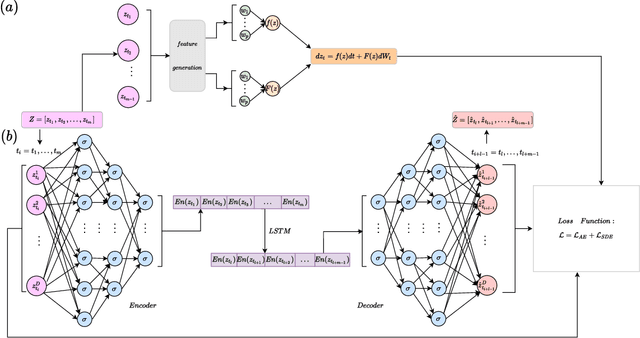
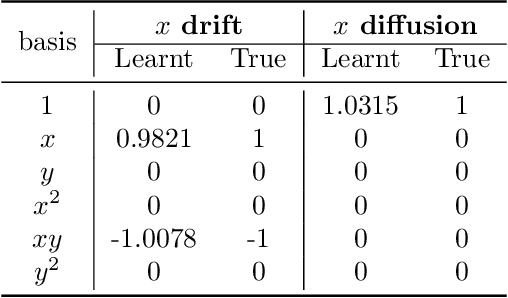
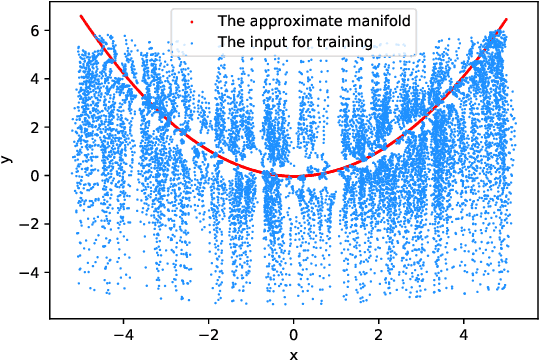
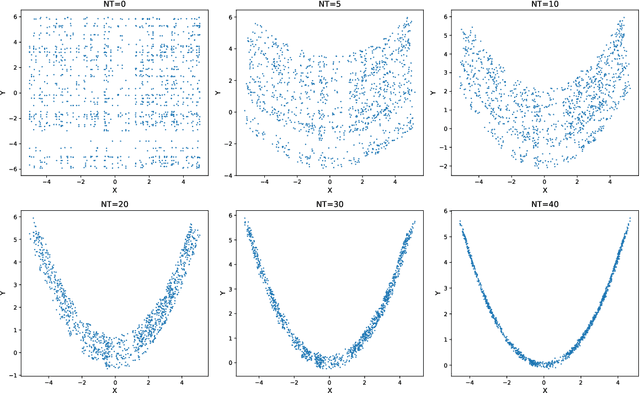
Multiscale stochastic dynamical systems have been widely adopted to scientific and engineering problems due to their capability of depicting complex phenomena in many real world applications. This work is devoted to investigating the effective reduced dynamics for a slow-fast stochastic dynamical system. Given observation data on a short-term period satisfying some unknown slow-fast stochastic system, we propose a novel algorithm including a neural network called Auto-SDE to learn invariant slow manifold. Our approach captures the evolutionary nature of a series of time-dependent autoencoder neural networks with the loss constructed from a discretized stochastic differential equation. Our algorithm is also proved to be accurate, stable and effective through numerical experiments under various evaluation metrics.