Xiaoli Chen
Constructing Custom Thermodynamics Using Deep Learning
Aug 08, 2023Abstract:One of the most exciting applications of AI is automated scientific discovery based on previously amassed data, coupled with restrictions provided by the known physical principles, including symmetries and conservation laws. Such automated hypothesis creation and verification can assist scientists in studying complex phenomena, where traditional physical intuition may fail. Of particular importance are complex dynamic systems where their time evolution is strongly influenced by varying external parameters. In this paper we develop a platform based on a generalised Onsager principle to learn macroscopic dynamical descriptions of arbitrary stochastic dissipative systems directly from observations of their microscopic trajectories. We focus on systems whose complexity and sheer sizes render complete microscopic description impractical, and constructing theoretical macroscopic models requires extensive domain knowledge or trial-and-error. Our machine learning approach addresses this by simultaneously constructing reduced thermodynamic coordinates and interpreting the dynamics on these coordinates. We demonstrate our method by studying theoretically and validating experimentally, the stretching of long polymer chains in an externally applied field. Specifically, we learn three interpretable thermodynamic coordinates and build a dynamical landscape of polymer stretching, including (1) the identification of stable and transition states and (2) the control of the stretching rate. We further demonstrate the universality of our approach by applying it to an unrelated problem in a different domain: constructing macroscopic dynamics for spatial epidemics, showing that our method addresses wide scientific and technological applications.
An Optimal Control Method to Compute the Most Likely Transition Path for Stochastic Dynamical Systems with Jumps
Mar 31, 2022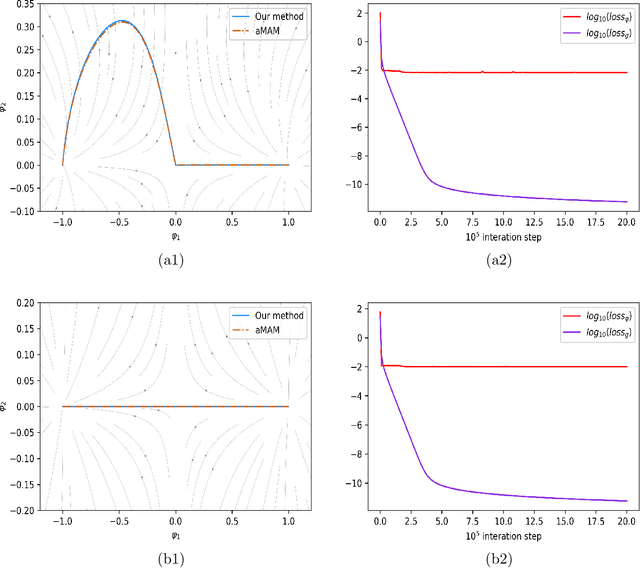
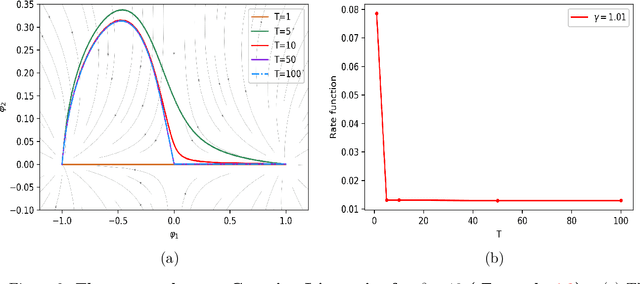
Abstract:Many complex real world phenomena exhibit abrupt, intermittent or jumping behaviors, which are more suitable to be described by stochastic differential equations under non-Gaussian L\'evy noise. Among these complex phenomena, the most likely transition paths between metastable states are important since these rare events may have high impact in certain scenarios. Based on the large deviation principle, the most likely transition path could be treated as the minimizer of the rate function upon paths that connect two points. One of the challenges to calculate the most likely transition path for stochastic dynamical systems under non-Gaussian L\'evy noise is that the associated rate function can not be explicitly expressed by paths. For this reason, we formulate an optimal control problem to obtain the optimal state as the most likely transition path. We then develop a neural network method to solve this issue. Several experiments are investigated for both Gaussian and non-Gaussian cases.
Solving Inverse Stochastic Problems from Discrete Particle Observations Using the Fokker-Planck Equation and Physics-informed Neural Networks
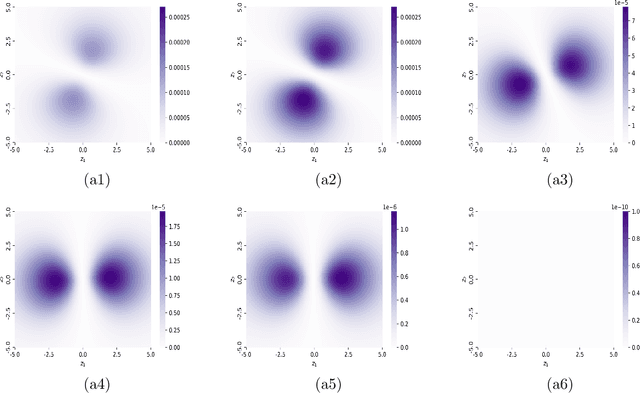
Aug 24, 2020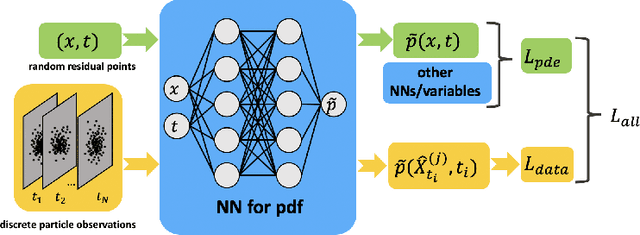
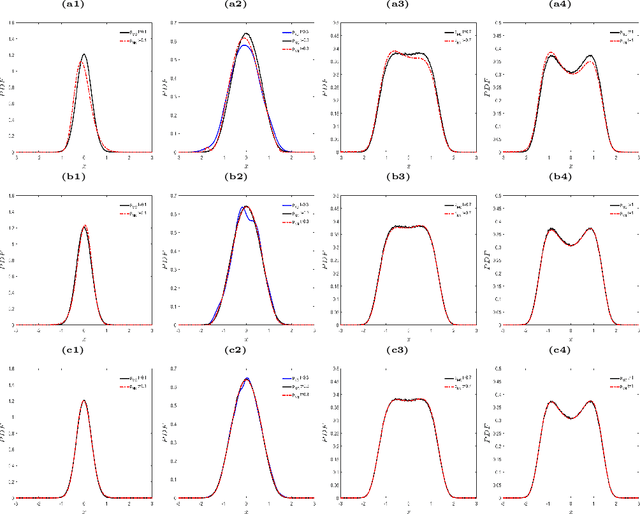
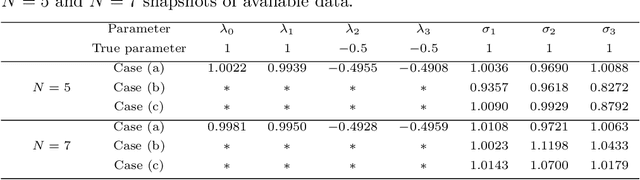
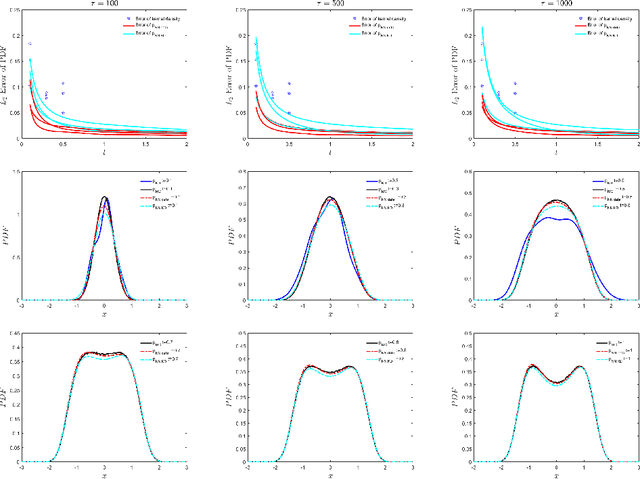
Abstract:The Fokker-Planck (FP) equation governing the evolution of the probability density function (PDF) is applicable to many disciplines but it requires specification of the coefficients for each case, which can be functions of space-time and not just constants, hence requiring the development of a data-driven modeling approach. When the data available is directly on the PDF, then there exist methods for inverse problems that can be employed to infer the coefficients and thus determine the FP equation and subsequently obtain its solution. Herein, we address a more realistic scenario, where only sparse data are given on the particles' positions at a few time instants, which are not sufficient to accurately construct directly the PDF even at those times from existing methods, e.g., kernel estimation algorithms. To this end, we develop a general framework based on physics-informed neural networks (PINNs) that introduces a new loss function using the Kullback-Leibler divergence to connect the stochastic samples with the FP equation, to simultaneously learn the equation and infer the multi-dimensional PDF at all times. In particular, we consider two types of inverse problems, type I where the FP equation is known but the initial PDF is unknown, and type II in which, in addition to unknown initial PDF, the drift and diffusion terms are also unknown. In both cases, we investigate problems with either Brownian or Levy noise or a combination of both. We demonstrate the new PINN framework in detail in the one-dimensional case (1D) but we also provide results for up to 5D demonstrating that we can infer both the FP equation and} dynamics simultaneously at all times with high accuracy using only very few discrete observations of the particles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge