An Optimal Control Method to Compute the Most Likely Transition Path for Stochastic Dynamical Systems with Jumps

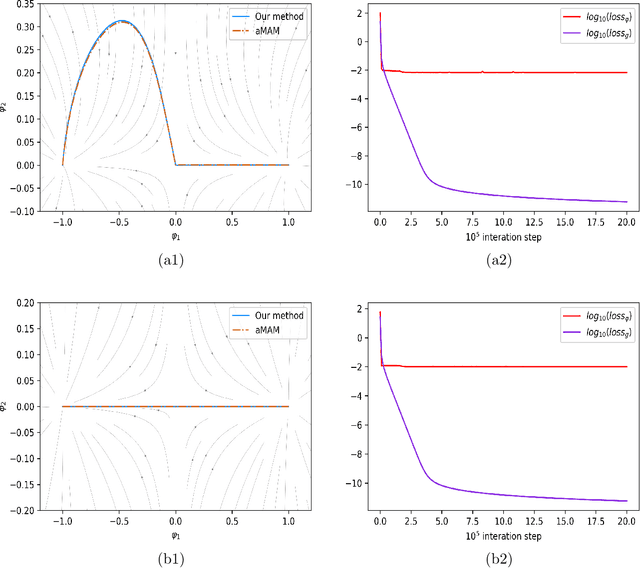
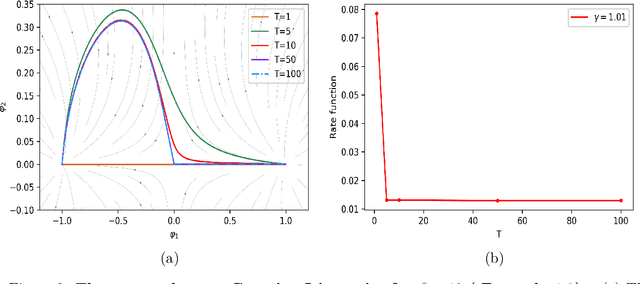
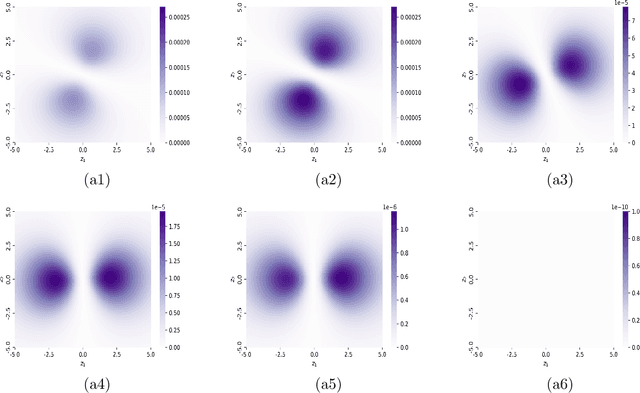
Many complex real world phenomena exhibit abrupt, intermittent or jumping behaviors, which are more suitable to be described by stochastic differential equations under non-Gaussian L\'evy noise. Among these complex phenomena, the most likely transition paths between metastable states are important since these rare events may have high impact in certain scenarios. Based on the large deviation principle, the most likely transition path could be treated as the minimizer of the rate function upon paths that connect two points. One of the challenges to calculate the most likely transition path for stochastic dynamical systems under non-Gaussian L\'evy noise is that the associated rate function can not be explicitly expressed by paths. For this reason, we formulate an optimal control problem to obtain the optimal state as the most likely transition path. We then develop a neural network method to solve this issue. Several experiments are investigated for both Gaussian and non-Gaussian cases.