Solving Inverse Stochastic Problems from Discrete Particle Observations Using the Fokker-Planck Equation and Physics-informed Neural Networks
Paper and Code
Aug 24, 2020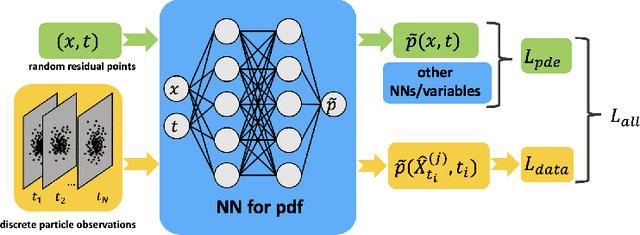
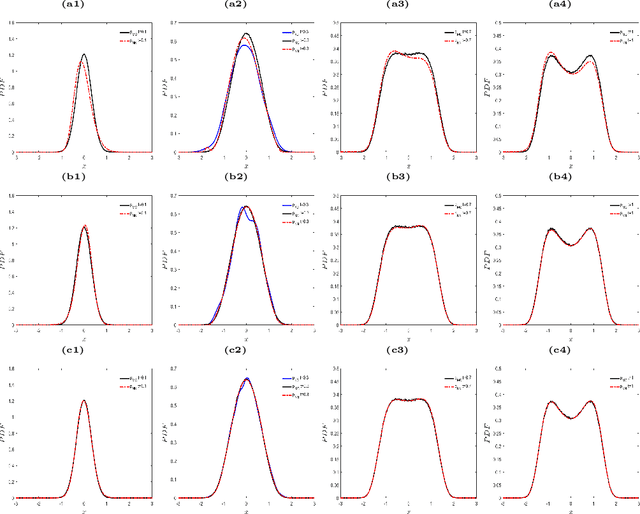
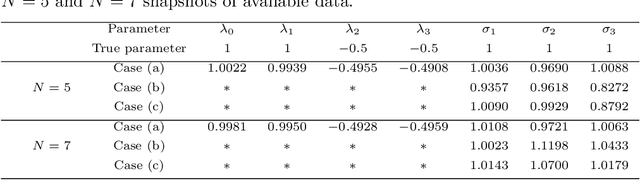
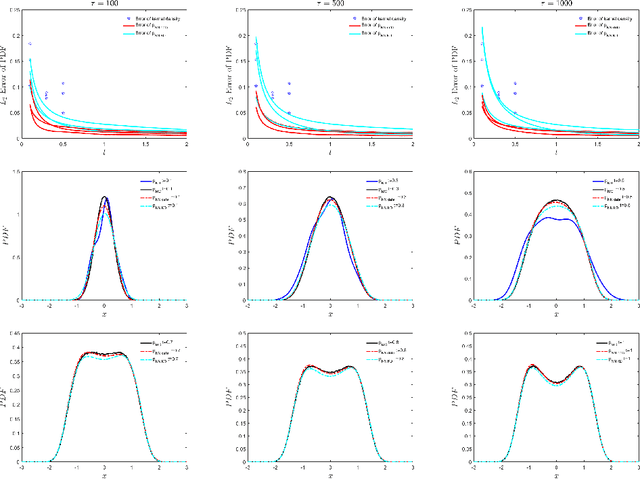
The Fokker-Planck (FP) equation governing the evolution of the probability density function (PDF) is applicable to many disciplines but it requires specification of the coefficients for each case, which can be functions of space-time and not just constants, hence requiring the development of a data-driven modeling approach. When the data available is directly on the PDF, then there exist methods for inverse problems that can be employed to infer the coefficients and thus determine the FP equation and subsequently obtain its solution. Herein, we address a more realistic scenario, where only sparse data are given on the particles' positions at a few time instants, which are not sufficient to accurately construct directly the PDF even at those times from existing methods, e.g., kernel estimation algorithms. To this end, we develop a general framework based on physics-informed neural networks (PINNs) that introduces a new loss function using the Kullback-Leibler divergence to connect the stochastic samples with the FP equation, to simultaneously learn the equation and infer the multi-dimensional PDF at all times. In particular, we consider two types of inverse problems, type I where the FP equation is known but the initial PDF is unknown, and type II in which, in addition to unknown initial PDF, the drift and diffusion terms are also unknown. In both cases, we investigate problems with either Brownian or Levy noise or a combination of both. We demonstrate the new PINN framework in detail in the one-dimensional case (1D) but we also provide results for up to 5D demonstrating that we can infer both the FP equation and} dynamics simultaneously at all times with high accuracy using only very few discrete observations of the particles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge