On Your Mark, Get Set, Predict! Modeling Continuous-Time Dynamics of Cascades for Information Popularity Prediction
Paper and Code
Sep 25, 2024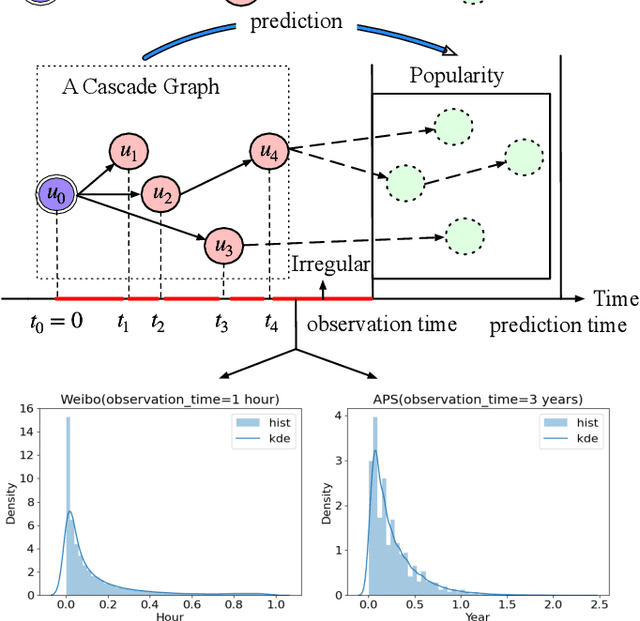
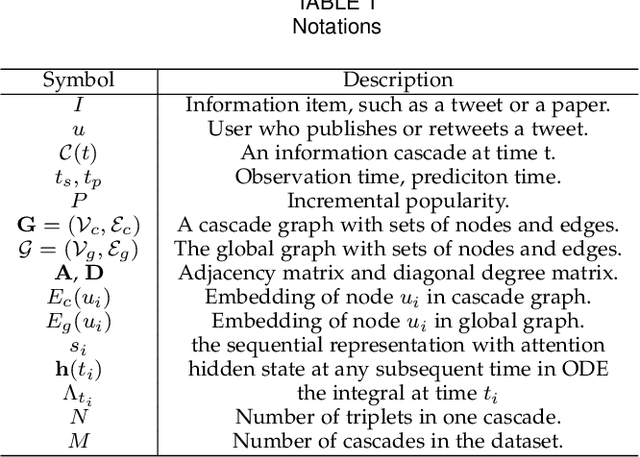
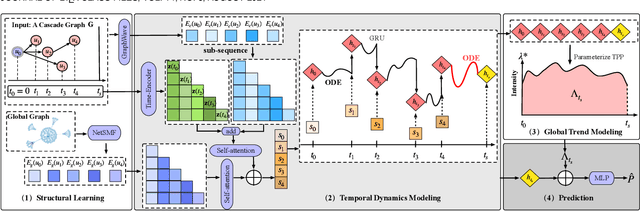

Information popularity prediction is important yet challenging in various domains, including viral marketing and news recommendations. The key to accurately predicting information popularity lies in subtly modeling the underlying temporal information diffusion process behind observed events of an information cascade, such as the retweets of a tweet. To this end, most existing methods either adopt recurrent networks to capture the temporal dynamics from the first to the last observed event or develop a statistical model based on self-exciting point processes to make predictions. However, information diffusion is intrinsically a complex continuous-time process with irregularly observed discrete events, which is oversimplified using recurrent networks as they fail to capture the irregular time intervals between events, or using self-exciting point processes as they lack flexibility to capture the complex diffusion process. Against this background, we propose ConCat, modeling the Continuous-time dynamics of Cascades for information popularity prediction. On the one hand, it leverages neural Ordinary Differential Equations (ODEs) to model irregular events of a cascade in continuous time based on the cascade graph and sequential event information. On the other hand, it considers cascade events as neural temporal point processes (TPPs) parameterized by a conditional intensity function which can also benefit the popularity prediction task. We conduct extensive experiments to evaluate ConCat on three real-world datasets. Results show that ConCat achieves superior performance compared to state-of-the-art baselines, yielding a 2.3%-33.2% improvement over the best-performing baselines across the three datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge