Stochastic parameter reduced-order model based on hybrid machine learning approaches
Paper and Code
Mar 24, 2024


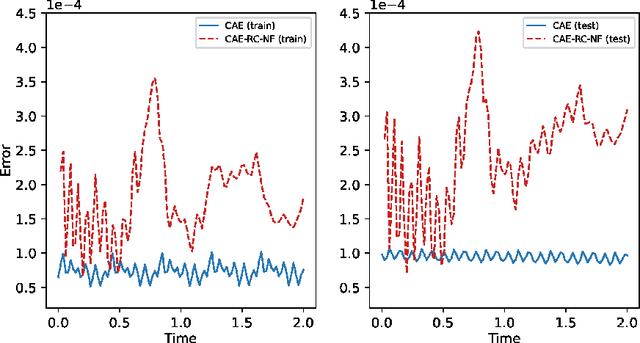
Establishing appropriate mathematical models for complex systems in natural phenomena not only helps deepen our understanding of nature but can also be used for state estimation and prediction. However, the extreme complexity of natural phenomena makes it extremely challenging to develop full-order models (FOMs) and apply them to studying many quantities of interest. In contrast, appropriate reduced-order models (ROMs) are favored due to their high computational efficiency and ability to describe the key dynamics and statistical characteristics of natural phenomena. Taking the viscous Burgers equation as an example, this paper constructs a Convolutional Autoencoder-Reservoir Computing-Normalizing Flow algorithm framework, where the Convolutional Autoencoder is used to construct latent space representations, and the Reservoir Computing-Normalizing Flow framework is used to characterize the evolution of latent state variables. In this way, a data-driven stochastic parameter reduced-order model is constructed to describe the complex system and its dynamic behavior.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge