A Machine Learning Framework for Computing the Most Probable Paths of Stochastic Dynamical Systems

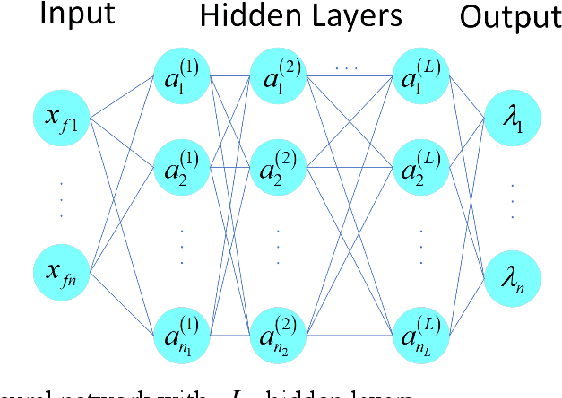
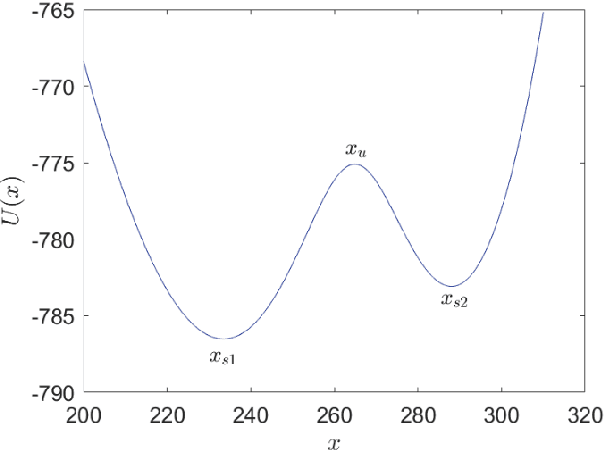
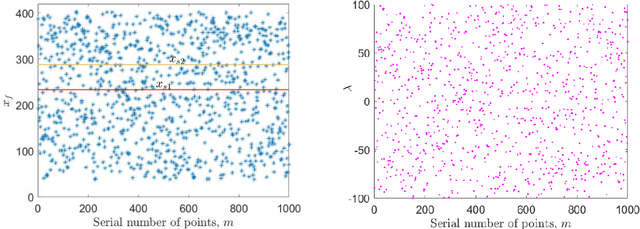
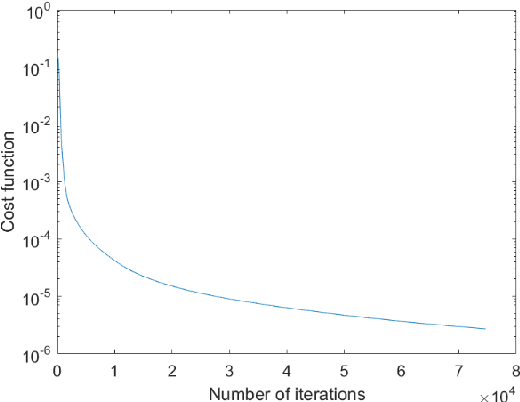
The emergence of transition phenomena between metastable states induced by noise plays a fundamental role in a broad range of nonlinear systems. The computation of the most probable paths is a key issue to understand the mechanism of transition behaviors. Shooting method is a common technique for this purpose, while losing its efficacy in high-dimensional systems. In the present work, we develop a machine learning framework to compute the most probable paths in the sense of Onsager-Machlup theory. Specifically, we reformulate the boundary value problem of Hamiltonian system and design a neural network to remedy the shortcomings of shooting method. The successful applications of our algorithms to several prototypical examples demonstrate its efficacy and accuracy for stochastic systems with both (Gaussian) Brownian noise and (non-Gaussian) L\'evy noise. This novel approach is effective in exploring the internal mechanisms of rare events triggered by random fluctuations in various scientific fields.