Deep importance sampling using tensor-trains with application to a priori and a posteriori rare event estimation

We propose a deep importance sampling method that is suitable for estimating rare event probabilities in high-dimensional problems. We approximate the optimal importance distribution in a general importance sampling problem as the pushforward of a reference distribution under a composition of order-preserving transformations, in which each transformation is formed by a squared tensor-train decomposition. The squared tensor-train decomposition provides a scalable ansatz for building order-preserving high-dimensional transformations via density approximations. The use of composition of maps moving along a sequence of bridging densities alleviates the difficulty of directly approximating concentrated density functions. To compute expectations over unnormalized probability distributions, we design a ratio estimator that estimates the normalizing constant using a separate importance distribution, again constructed via a composition of transformations in tensor-train format. This offers better theoretical variance reduction compared with self-normalized importance sampling, and thus opens the door to efficient computation of rare event probabilities in Bayesian inference problems. Numerical experiments on problems constrained by differential equations show little to no increase in the computational complexity with the event probability going to zero, and allow to compute hitherto unattainable estimates of rare event probabilities for complex, high-dimensional posterior densities.

HINT: Hierarchical Invertible Neural Transport for General and Sequential Bayesian inference

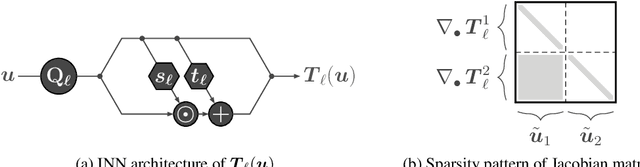
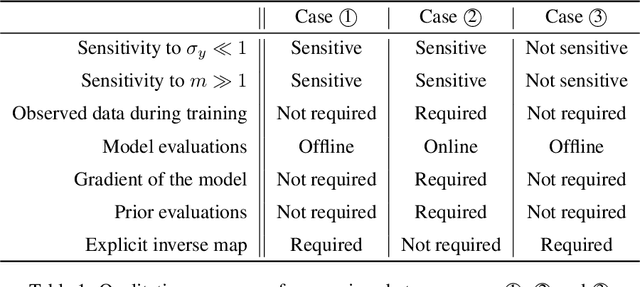
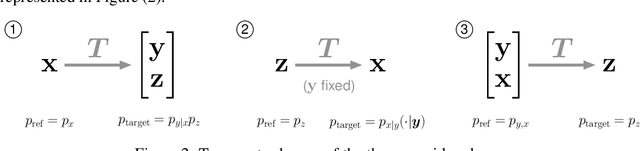
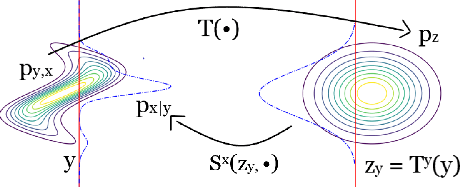
In this paper, we introduce Hierarchical Invertible Neural Transport (HINT), an algorithm that merges Invertible Neural Networks and optimal transport to sample from a posterior distribution in a Bayesian framework. This method exploits a hierarchical architecture to construct a Knothe-Rosenblatt transport map between an arbitrary density and the joint density of hidden variables and observations. After training the map, samples from the posterior can be immediately recovered for any contingent observation. Any underlying model evaluation can be performed fully offline from training without the need of a model-gradient. Furthermore, no analytical evaluation of the prior is necessary, which makes HINT an ideal candidate for sequential Bayesian inference. We demonstrate the efficacy of HINT on two numerical experiments.

A Stein variational Newton method

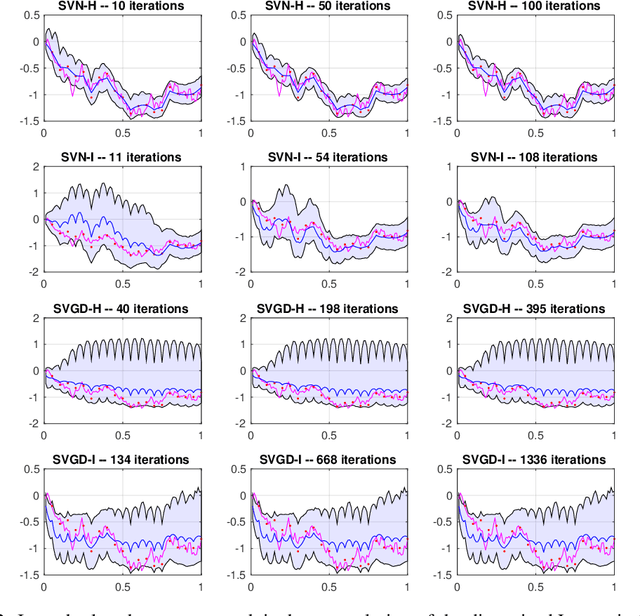
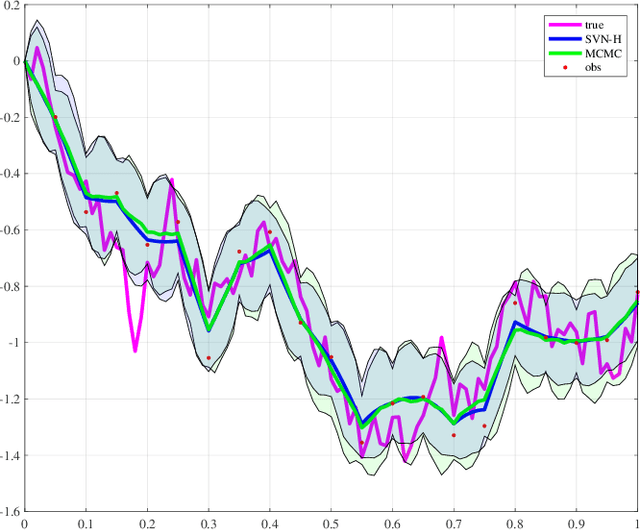
Stein variational gradient descent (SVGD) was recently proposed as a general purpose nonparametric variational inference algorithm [Liu & Wang, NIPS 2016]: it minimizes the Kullback-Leibler divergence between the target distribution and its approximation by implementing a form of functional gradient descent on a reproducing kernel Hilbert space. In this paper, we accelerate and generalize the SVGD algorithm by including second-order information, thereby approximating a Newton-like iteration in function space. We also show how second-order information can lead to more effective choices of kernel. We observe significant computational gains over the original SVGD algorithm in multiple test cases.