Jakob Kruse
Towards Learned Emulation of Interannual Water Isotopologue Variations in General Circulation Models
Jan 31, 2023Abstract:Simulating abundances of stable water isotopologues, i.e. molecules differing in their isotopic composition, within climate models allows for comparisons with proxy data and, thus, for testing hypotheses about past climate and validating climate models under varying climatic conditions. However, many models are run without explicitly simulating water isotopologues. We investigate the possibility to replace the explicit physics-based simulation of oxygen isotopic composition in precipitation using machine learning methods. These methods estimate isotopic composition at each time step for given fields of surface temperature and precipitation amount. We implement convolutional neural networks (CNNs) based on the successful UNet architecture and test whether a spherical network architecture outperforms the naive approach of treating Earth's latitude-longitude grid as a flat image. Conducting a case study on a last millennium run with the iHadCM3 climate model, we find that roughly 40\% of the temporal variance in the isotopic composition is explained by the emulations on interannual and monthly timescale, with spatially varying emulation quality. A modified version of the standard UNet architecture for flat images yields results that are equally good as the predictions by the spherical CNN. We test generalization to last millennium runs of other climate models and find that while the tested deep learning methods yield the best results on iHadCM3 data, the performance drops when predicting on other models and is comparable to simple pixel-wise linear regression. An extended choice of predictor variables and improving the robustness of learned climate--oxygen isotope relationships should be explored in future work.
Conditional Invertible Neural Networks for Diverse Image-to-Image Translation
May 05, 2021



Abstract:We introduce a new architecture called a conditional invertible neural network (cINN), and use it to address the task of diverse image-to-image translation for natural images. This is not easily possible with existing INN models due to some fundamental limitations. The cINN combines the purely generative INN model with an unconstrained feed-forward network, which efficiently preprocesses the conditioning image into maximally informative features. All parameters of a cINN are jointly optimized with a stable, maximum likelihood-based training procedure. Even though INN-based models have received far less attention in the literature than GANs, they have been shown to have some remarkable properties absent in GANs, e.g. apparent immunity to mode collapse. We find that our cINNs leverage these properties for image-to-image translation, demonstrated on day to night translation and image colorization. Furthermore, we take advantage of our bidirectional cINN architecture to explore and manipulate emergent properties of the latent space, such as changing the image style in an intuitive way.
Benchmarking Invertible Architectures on Inverse Problems
Jan 26, 2021



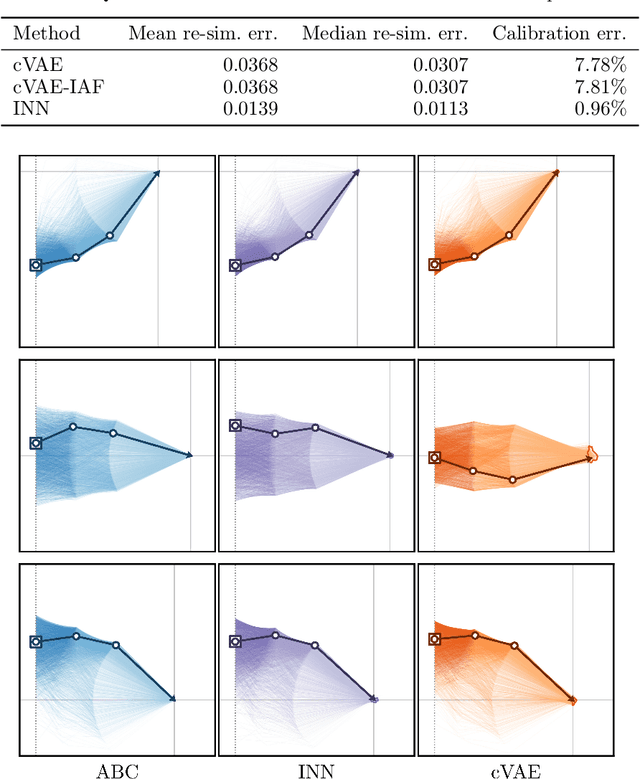
Abstract:Recent work demonstrated that flow-based invertible neural networks are promising tools for solving ambiguous inverse problems. Following up on this, we investigate how ten invertible architectures and related models fare on two intuitive, low-dimensional benchmark problems, obtaining the best results with coupling layers and simple autoencoders. We hope that our initial efforts inspire other researchers to evaluate their invertible architectures in the same setting and put forth additional benchmarks, so our evaluation may eventually grow into an official community challenge.
Technical report: Training Mixture Density Networks with full covariance matrices
Mar 04, 2020
Abstract:Mixture Density Networks are a tried and tested tool for modelling conditional probability distributions. As such, they constitute a great baseline for novel approaches to this problem. In the standard formulation, an MDN takes some input and outputs parameters for a Gaussian mixture model with restrictions on the mixture components' covariance. Since covariance between random variables is a central issue in the conditional modeling problems we were investigating, I derived and implemented an MDN formulation with unrestricted covariances. It is likely that this has been done before, but I could not find any resources online. For this reason, I have documented my approach in the form of this technical report, in hopes that it may be useful to others facing a similar situation.
Guided Image Generation with Conditional Invertible Neural Networks
Jul 10, 2019



Abstract:In this work, we address the task of natural image generation guided by a conditioning input. We introduce a new architecture called conditional invertible neural network (cINN). The cINN combines the purely generative INN model with an unconstrained feed-forward network, which efficiently preprocesses the conditioning input into useful features. All parameters of the cINN are jointly optimized with a stable, maximum likelihood-based training procedure. By construction, the cINN does not experience mode collapse and generates diverse samples, in contrast to e.g. cGANs. At the same time our model produces sharp images since no reconstruction loss is required, in contrast to e.g. VAEs. We demonstrate these properties for the tasks of MNIST digit generation and image colorization. Furthermore, we take advantage of our bi-directional cINN architecture to explore and manipulate emergent properties of the latent space, such as changing the image style in an intuitive way.
HINT: Hierarchical Invertible Neural Transport for General and Sequential Bayesian inference
May 25, 2019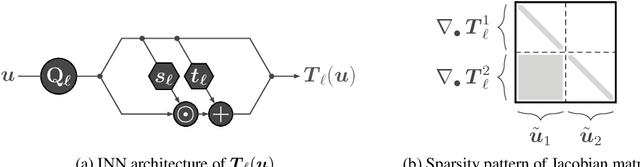
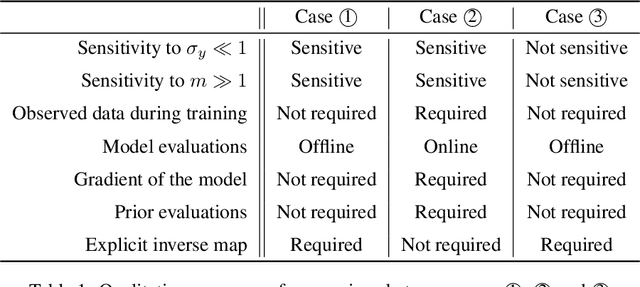
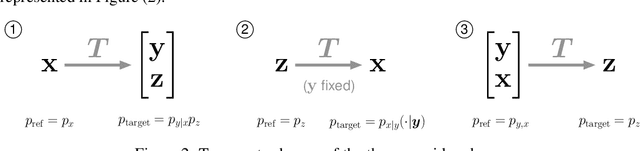
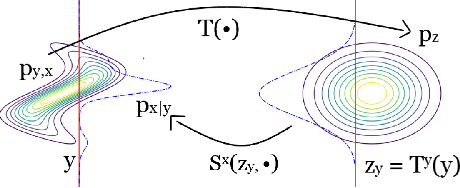
Abstract:In this paper, we introduce Hierarchical Invertible Neural Transport (HINT), an algorithm that merges Invertible Neural Networks and optimal transport to sample from a posterior distribution in a Bayesian framework. This method exploits a hierarchical architecture to construct a Knothe-Rosenblatt transport map between an arbitrary density and the joint density of hidden variables and observations. After training the map, samples from the posterior can be immediately recovered for any contingent observation. Any underlying model evaluation can be performed fully offline from training without the need of a model-gradient. Furthermore, no analytical evaluation of the prior is necessary, which makes HINT an ideal candidate for sequential Bayesian inference. We demonstrate the efficacy of HINT on two numerical experiments.
Uncertainty-aware performance assessment of optical imaging modalities with invertible neural networks
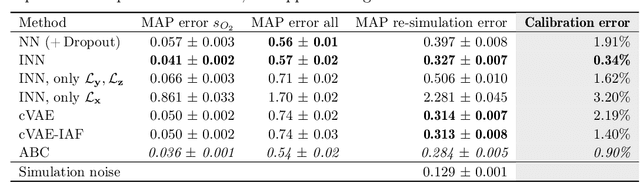
Mar 08, 2019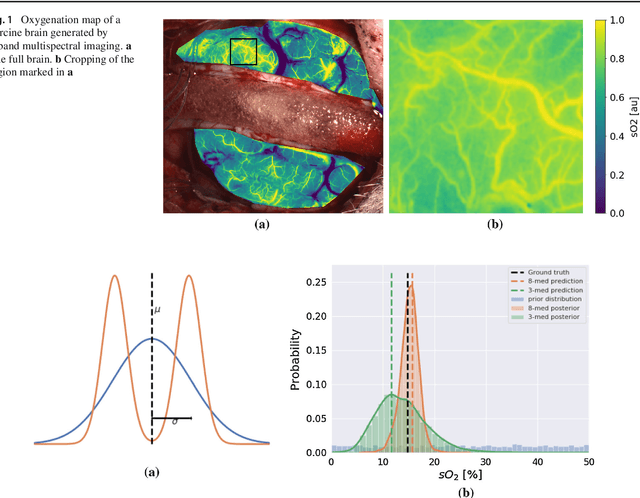


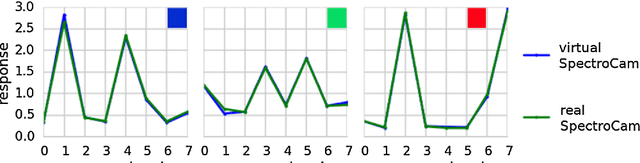
Abstract:Purpose: Optical imaging is evolving as a key technique for advanced sensing in the operating room. Recent research has shown that machine learning algorithms can be used to address the inverse problem of converting pixel-wise multispectral reflectance measurements to underlying tissue parameters, such as oxygenation. Assessment of the specific hardware used in conjunction with such algorithms, however, has not properly addressed the possibility that the problem may be ill-posed. Methods: We present a novel approach to the assessment of optical imaging modalities, which is sensitive to the different types of uncertainties that may occur when inferring tissue parameters. Based on the concept of invertible neural networks, our framework goes beyond point estimates and maps each multispectral measurement to a full posterior probability distribution which is capable of representing ambiguity in the solution via multiple modes. Performance metrics for a hardware setup can then be computed from the characteristics of the posteriors. Results: Application of the assessment framework to the specific use case of camera selection for physiological parameter estimation yields the following insights: (1) Estimation of tissue oxygenation from multispectral images is a well-posed problem, while (2) blood volume fraction may not be recovered without ambiguity. (3) In general, ambiguity may be reduced by increasing the number of spectral bands in the camera. Conclusion: Our method could help to optimize optical camera design in an application-specific manner.
Analyzing Inverse Problems with Invertible Neural Networks
Sep 10, 2018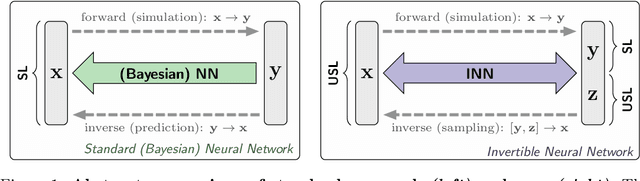
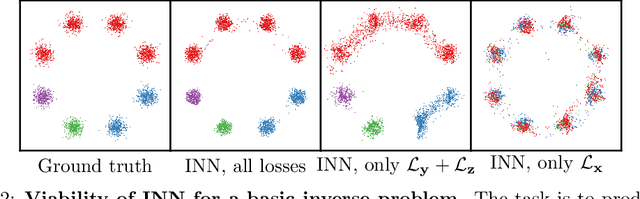
Abstract:In many tasks, in particular in natural science, the goal is to determine hidden system parameters from a set of measurements. Often, the forward process from parameter- to measurement-space is a well-defined function, whereas the inverse problem is ambiguous: one measurement may map to multiple different sets of parameters. In this setting, the posterior parameter distribution, conditioned on an input measurement, has to be determined. We argue that a particular class of neural networks is well suited for this task -- so-called Invertible Neural Networks (INNs). Although INNs are not new, they have, so far, received little attention in literature. While classical neural networks attempt to solve the ambiguous inverse problem directly, INNs are able to learn it jointly with the well-defined forward process, using additional latent output variables to capture the information otherwise lost. Given a specific measurement and sampled latent variables, the inverse pass of the INN provides a full distribution over parameter space. We verify experimentally, on artificial data and real-world problems from astrophysics and medicine, that INNs are a powerful analysis tool to find multi-modalities in parameter space, to uncover parameter correlations, and to identify unrecoverable parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge