Exoplanet Characterization using Conditional Invertible Neural Networks

The characterization of an exoplanet's interior is an inverse problem, which requires statistical methods such as Bayesian inference in order to be solved. Current methods employ Markov Chain Monte Carlo (MCMC) sampling to infer the posterior probability of planetary structure parameters for a given exoplanet. These methods are time consuming since they require the calculation of a large number of planetary structure models. To speed up the inference process when characterizing an exoplanet, we propose to use conditional invertible neural networks (cINNs) to calculate the posterior probability of the internal structure parameters. cINNs are a special type of neural network which excel in solving inverse problems. We constructed a cINN using FrEIA, which was then trained on a database of $5.6\cdot 10^6$ internal structure models to recover the inverse mapping between internal structure parameters and observable features (i.e., planetary mass, planetary radius and composition of the host star). The cINN method was compared to a Metropolis-Hastings MCMC. For that we repeated the characterization of the exoplanet K2-111 b, using both the MCMC method and the trained cINN. We show that the inferred posterior probability of the internal structure parameters from both methods are very similar, with the biggest differences seen in the exoplanet's water content. Thus cINNs are a possible alternative to the standard time-consuming sampling methods. Indeed, using cINNs allows for orders of magnitude faster inference of an exoplanet's composition than what is possible using an MCMC method, however, it still requires the computation of a large database of internal structures to train the cINN. Since this database is only computed once, we found that using a cINN is more efficient than an MCMC, when more than 10 exoplanets are characterized using the same cINN.

Analyzing Inverse Problems with Invertible Neural Networks

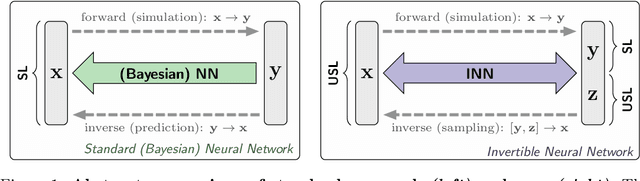
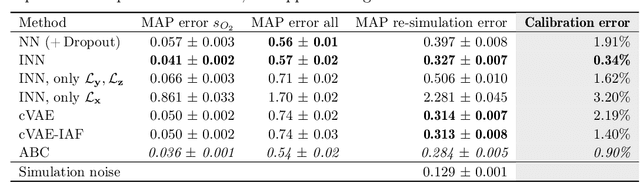
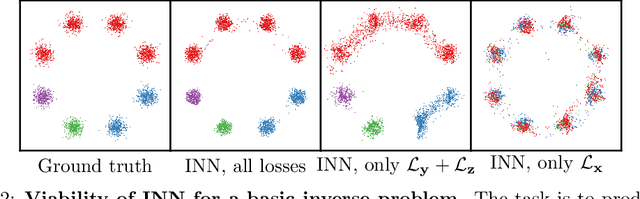
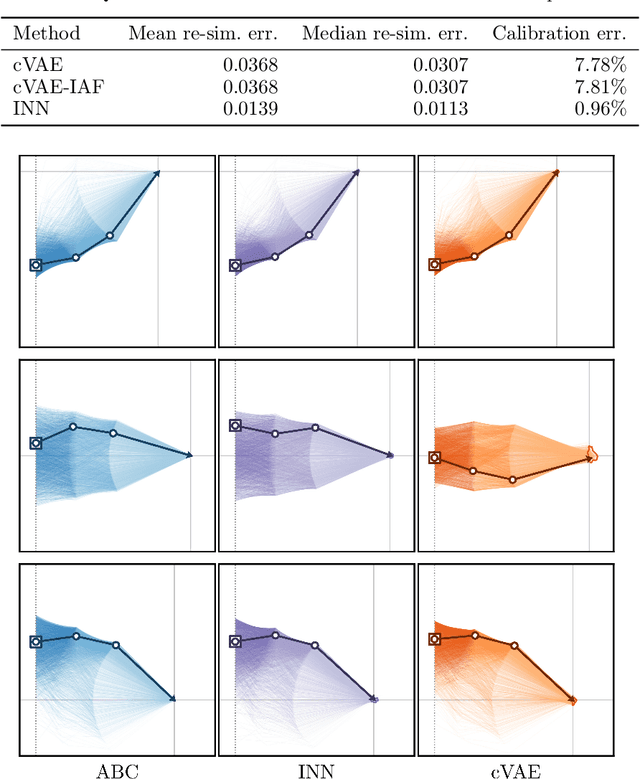
In many tasks, in particular in natural science, the goal is to determine hidden system parameters from a set of measurements. Often, the forward process from parameter- to measurement-space is a well-defined function, whereas the inverse problem is ambiguous: one measurement may map to multiple different sets of parameters. In this setting, the posterior parameter distribution, conditioned on an input measurement, has to be determined. We argue that a particular class of neural networks is well suited for this task -- so-called Invertible Neural Networks (INNs). Although INNs are not new, they have, so far, received little attention in literature. While classical neural networks attempt to solve the ambiguous inverse problem directly, INNs are able to learn it jointly with the well-defined forward process, using additional latent output variables to capture the information otherwise lost. Given a specific measurement and sampled latent variables, the inverse pass of the INN provides a full distribution over parameter space. We verify experimentally, on artificial data and real-world problems from astrophysics and medicine, that INNs are a powerful analysis tool to find multi-modalities in parameter space, to uncover parameter correlations, and to identify unrecoverable parameters.