Cost-Effective Hallucination Detection for LLMs

Large language models (LLMs) can be prone to hallucinations - generating unreliable outputs that are unfaithful to their inputs, external facts or internally inconsistent. In this work, we address several challenges for post-hoc hallucination detection in production settings. Our pipeline for hallucination detection entails: first, producing a confidence score representing the likelihood that a generated answer is a hallucination; second, calibrating the score conditional on attributes of the inputs and candidate response; finally, performing detection by thresholding the calibrated score. We benchmark a variety of state-of-the-art scoring methods on different datasets, encompassing question answering, fact checking, and summarization tasks. We employ diverse LLMs to ensure a comprehensive assessment of performance. We show that calibrating individual scoring methods is critical for ensuring risk-aware downstream decision making. Based on findings that no individual score performs best in all situations, we propose a multi-scoring framework, which combines different scores and achieves top performance across all datasets. We further introduce cost-effective multi-scoring, which can match or even outperform more expensive detection methods, while significantly reducing computational overhead.

Multicalibration for Confidence Scoring in LLMs

This paper proposes the use of "multicalibration" to yield interpretable and reliable confidence scores for outputs generated by large language models (LLMs). Multicalibration asks for calibration not just marginally, but simultaneously across various intersecting groupings of the data. We show how to form groupings for prompt/completion pairs that are correlated with the probability of correctness via two techniques: clustering within an embedding space, and "self-annotation" - querying the LLM by asking it various yes-or-no questions about the prompt. We also develop novel variants of multicalibration algorithms that offer performance improvements by reducing their tendency to overfit. Through systematic benchmarking across various question answering datasets and LLMs, we show how our techniques can yield confidence scores that provide substantial improvements in fine-grained measures of both calibration and accuracy compared to existing methods.

Fortuna: A Library for Uncertainty Quantification in Deep Learning

We present Fortuna, an open-source library for uncertainty quantification in deep learning. Fortuna supports a range of calibration techniques, such as conformal prediction that can be applied to any trained neural network to generate reliable uncertainty estimates, and scalable Bayesian inference methods that can be applied to Flax-based deep neural networks trained from scratch for improved uncertainty quantification and accuracy. By providing a coherent framework for advanced uncertainty quantification methods, Fortuna simplifies the process of benchmarking and helps practitioners build robust AI systems.

Uncertainty Calibration in Bayesian Neural Networks via Distance-Aware Priors

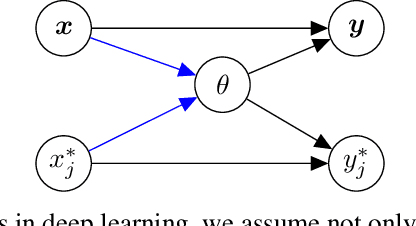
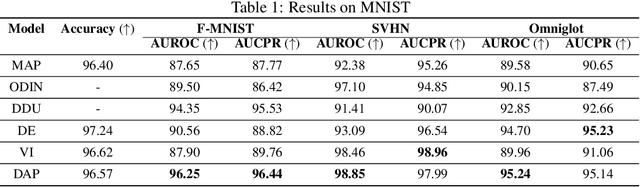
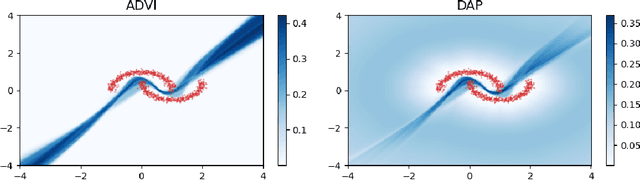
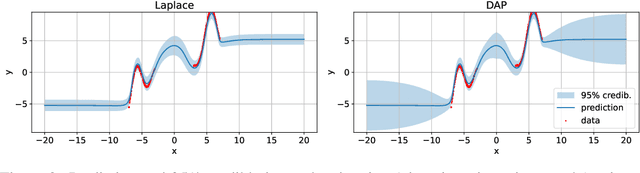
As we move away from the data, the predictive uncertainty should increase, since a great variety of explanations are consistent with the little available information. We introduce Distance-Aware Prior (DAP) calibration, a method to correct overconfidence of Bayesian deep learning models outside of the training domain. We define DAPs as prior distributions over the model parameters that depend on the inputs through a measure of their distance from the training set. DAP calibration is agnostic to the posterior inference method, and it can be performed as a post-processing step. We demonstrate its effectiveness against several baselines in a variety of classification and regression problems, including benchmarks designed to test the quality of predictive distributions away from the data.

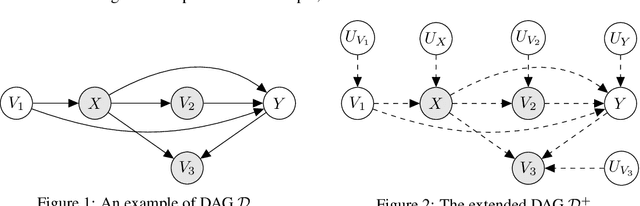
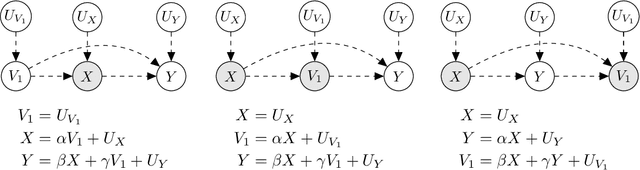
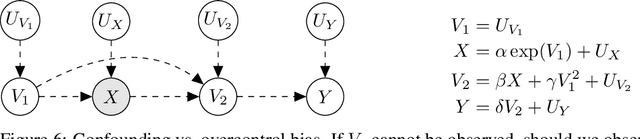
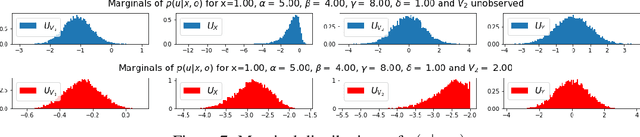
Causal Bias Quantification for Continuous Treatment

In this work we develop a novel characterization of marginal causal effect and causal bias in the continuous treatment setting. We show they can be expressed as an expectation with respect to a conditional probability distribution, which can be estimated via standard statistical and probabilistic methods. All terms in the expectations can be computed via automatic differentiation, also for highly non-linear models. We further develop a new complete criterion for identifiability of causal effects via covariate adjustment, showing the bias equals zero if the criterion is met. We study the effectiveness of our framework in three different scenarios: linear models under confounding, overcontrol and endogenous selection bias; a non-linear model where full identifiability cannot be achieved because of missing data; a simulated medical study of statins and atherosclerotic cardiovascular disease.

HINT: Hierarchical Invertible Neural Transport for General and Sequential Bayesian inference

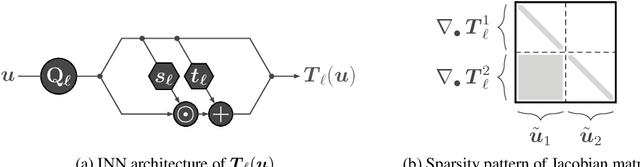
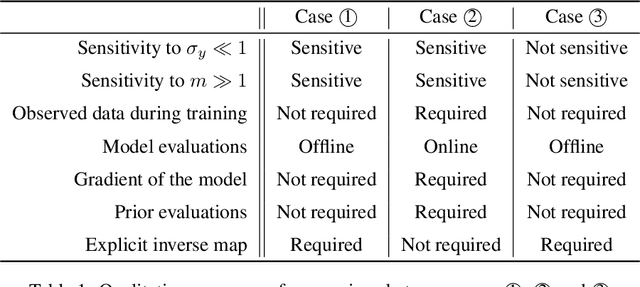
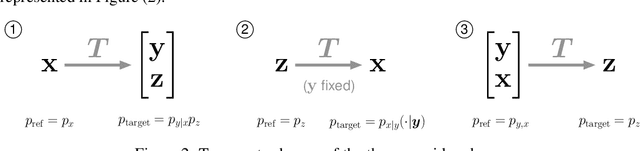
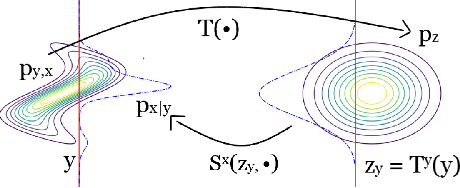
In this paper, we introduce Hierarchical Invertible Neural Transport (HINT), an algorithm that merges Invertible Neural Networks and optimal transport to sample from a posterior distribution in a Bayesian framework. This method exploits a hierarchical architecture to construct a Knothe-Rosenblatt transport map between an arbitrary density and the joint density of hidden variables and observations. After training the map, samples from the posterior can be immediately recovered for any contingent observation. Any underlying model evaluation can be performed fully offline from training without the need of a model-gradient. Furthermore, no analytical evaluation of the prior is necessary, which makes HINT an ideal candidate for sequential Bayesian inference. We demonstrate the efficacy of HINT on two numerical experiments.

Stein Variational Online Changepoint Detection with Applications to Hawkes Processes and Neural Networks

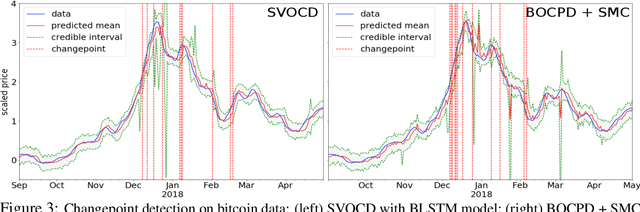
Bayesian online changepoint detection (BOCPD) (Adams & MacKay, 2007) offers a rigorous and viable way to identity changepoints in complex systems. In this work, we introduce a Stein variational online changepoint detection (SVOCD) method to provide a computationally tractable generalization of BOCPD beyond the exponential family of probability distributions. We integrate the recently developed Stein variational Newton (SVN) method (Detommaso et al., 2018) and BOCPD to offer a full online Bayesian treatment for a large number of situations with significant importance in practice. We apply the resulting method to two challenging and novel applications: Hawkes processes and long short-term memory (LSTM) neural networks. In both cases, we successfully demonstrate the efficacy of our method on real data.

A Stein variational Newton method

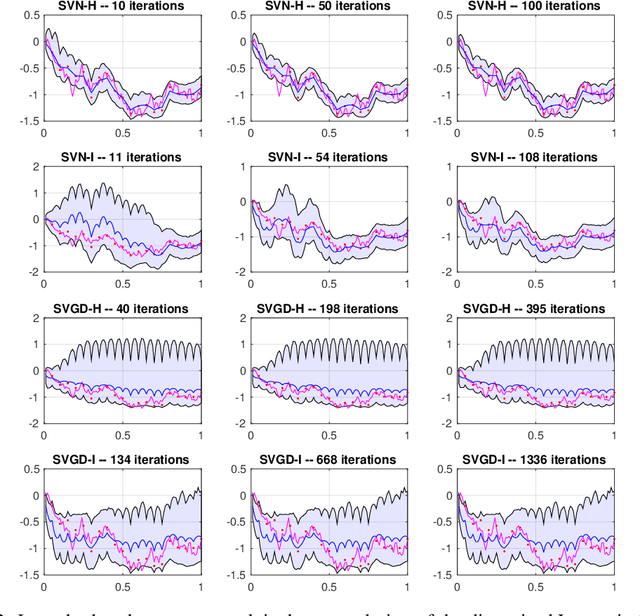
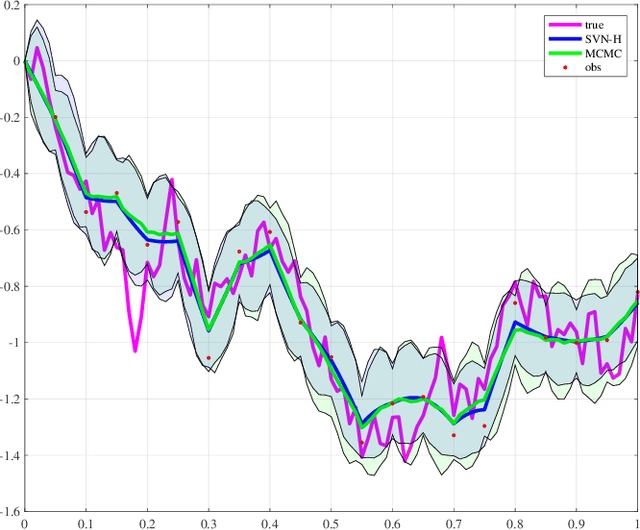
Stein variational gradient descent (SVGD) was recently proposed as a general purpose nonparametric variational inference algorithm [Liu & Wang, NIPS 2016]: it minimizes the Kullback-Leibler divergence between the target distribution and its approximation by implementing a form of functional gradient descent on a reproducing kernel Hilbert space. In this paper, we accelerate and generalize the SVGD algorithm by including second-order information, thereby approximating a Newton-like iteration in function space. We also show how second-order information can lead to more effective choices of kernel. We observe significant computational gains over the original SVGD algorithm in multiple test cases.