Stein Variational Online Changepoint Detection with Applications to Hawkes Processes and Neural Networks
Paper and Code
Jan 23, 2019


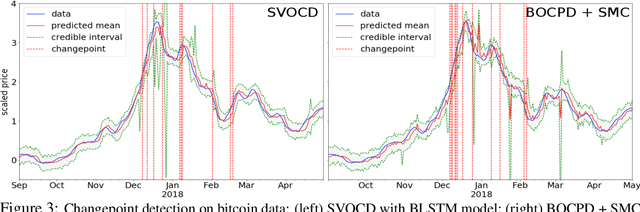
Bayesian online changepoint detection (BOCPD) (Adams & MacKay, 2007) offers a rigorous and viable way to identity changepoints in complex systems. In this work, we introduce a Stein variational online changepoint detection (SVOCD) method to provide a computationally tractable generalization of BOCPD beyond the exponential family of probability distributions. We integrate the recently developed Stein variational Newton (SVN) method (Detommaso et al., 2018) and BOCPD to offer a full online Bayesian treatment for a large number of situations with significant importance in practice. We apply the resulting method to two challenging and novel applications: Hawkes processes and long short-term memory (LSTM) neural networks. In both cases, we successfully demonstrate the efficacy of our method on real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge