Causal Bias Quantification for Continuous Treatment
Paper and Code
Jun 17, 2021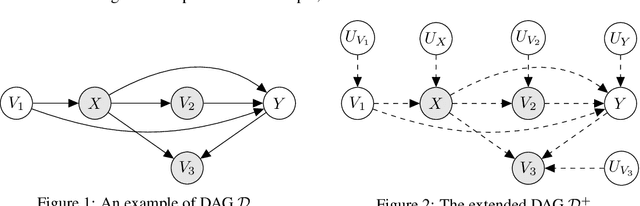
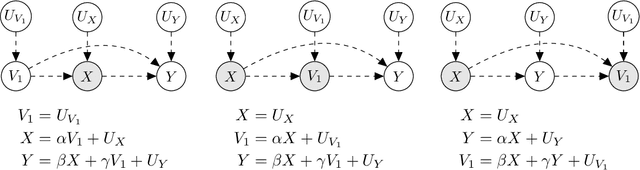
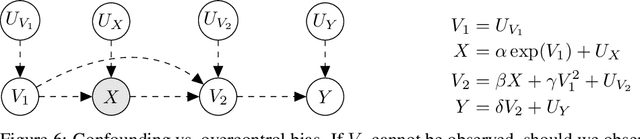
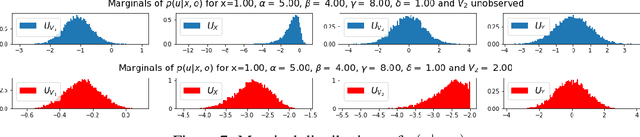
In this work we develop a novel characterization of marginal causal effect and causal bias in the continuous treatment setting. We show they can be expressed as an expectation with respect to a conditional probability distribution, which can be estimated via standard statistical and probabilistic methods. All terms in the expectations can be computed via automatic differentiation, also for highly non-linear models. We further develop a new complete criterion for identifiability of causal effects via covariate adjustment, showing the bias equals zero if the criterion is met. We study the effectiveness of our framework in three different scenarios: linear models under confounding, overcontrol and endogenous selection bias; a non-linear model where full identifiability cannot be achieved because of missing data; a simulated medical study of statins and atherosclerotic cardiovascular disease.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge