Victor Chernozhukov
Automatic debiased machine learning and sensitivity analysis for sample selection models
Jan 13, 2026Abstract:In this paper, we extend the Riesz representation framework to causal inference under sample selection, where both treatment assignment and outcome observability are non-random. Formulating the problem in terms of a Riesz representer enables stable estimation and a transparent decomposition of omitted variable bias into three interpretable components: a data-identified scale factor, outcome confounding strength, and selection confounding strength. For estimation, we employ the ForestRiesz estimator, which accounts for selective outcome observability while avoiding the instability associated with direct propensity score inversion. We assess finite-sample performance through a simulation study and show that conventional double machine learning approaches can be highly sensitive to tuning parameters due to their reliance on inverse probability weighting, whereas the ForestRiesz estimator delivers more stable performance by leveraging automatic debiased machine learning. In an empirical application to the gender wage gap in the U.S., we find that our ForestRiesz approach yields larger treatment effect estimates than a standard double machine learning approach, suggesting that ignoring sample selection leads to an underestimation of the gender wage gap. Sensitivity analysis indicates that implausibly strong unobserved confounding would be required to overturn our results. Overall, our approach provides a unified, robust, and computationally attractive framework for causal inference under sample selection.
An Introduction to Double/Debiased Machine Learning
Apr 11, 2025Abstract:This paper provides a practical introduction to Double/Debiased Machine Learning (DML). DML provides a general approach to performing inference about a target parameter in the presence of nuisance parameters. The aim of DML is to reduce the impact of nuisance parameter estimation on estimators of the parameter of interest. We describe DML and its two essential components: Neyman orthogonality and cross-fitting. We highlight that DML reduces functional form dependence and accommodates the use of complex data types, such as text data. We illustrate its application through three empirical examples that demonstrate DML's applicability in cross-sectional and panel settings.
Adventures in Demand Analysis Using AI
Dec 31, 2024

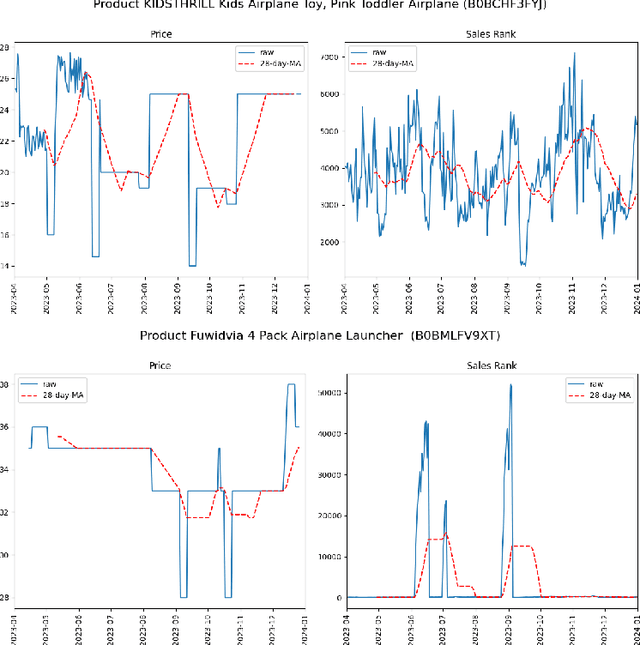

Abstract:This paper advances empirical demand analysis by integrating multimodal product representations derived from artificial intelligence (AI). Using a detailed dataset of toy cars on \textit{Amazon.com}, we combine text descriptions, images, and tabular covariates to represent each product using transformer-based embedding models. These embeddings capture nuanced attributes, such as quality, branding, and visual characteristics, that traditional methods often struggle to summarize. Moreover, we fine-tune these embeddings for causal inference tasks. We show that the resulting embeddings substantially improve the predictive accuracy of sales ranks and prices and that they lead to more credible causal estimates of price elasticity. Notably, we uncover strong heterogeneity in price elasticity driven by these product-specific features. Our findings illustrate that AI-driven representations can enrich and modernize empirical demand analysis. The insights generated may also prove valuable for applied causal inference more broadly.
Automatic Doubly Robust Forests
Dec 10, 2024Abstract:This paper proposes the automatic Doubly Robust Random Forest (DRRF) algorithm for estimating the conditional expectation of a moment functional in the presence of high-dimensional nuisance functions. DRRF combines the automatic debiasing framework using the Riesz representer (Chernozhukov et al., 2022) with non-parametric, forest-based estimation methods for the conditional moment (Athey et al., 2019; Oprescu et al., 2019). In contrast to existing methods, DRRF does not require prior knowledge of the form of the debiasing term nor impose restrictive parametric or semi-parametric assumptions on the target quantity. Additionally, it is computationally efficient for making predictions at multiple query points and significantly reduces runtime compared to methods such as Orthogonal Random Forest (Oprescu et al., 2019). We establish the consistency and asymptotic normality results of DRRF estimator under general assumptions, allowing for the construction of valid confidence intervals. Through extensive simulations in heterogeneous treatment effect (HTE) estimation, we demonstrate the superior performance of DRRF over benchmark approaches in terms of estimation accuracy, robustness, and computational efficiency.
Applied Causal Inference Powered by ML and AI
Mar 04, 2024



Abstract:An introduction to the emerging fusion of machine learning and causal inference. The book presents ideas from classical structural equation models (SEMs) and their modern AI equivalent, directed acyclical graphs (DAGs) and structural causal models (SCMs), and covers Double/Debiased Machine Learning methods to do inference in such models using modern predictive tools.
Hyperparameter Tuning for Causal Inference with Double Machine Learning: A Simulation Study
Feb 07, 2024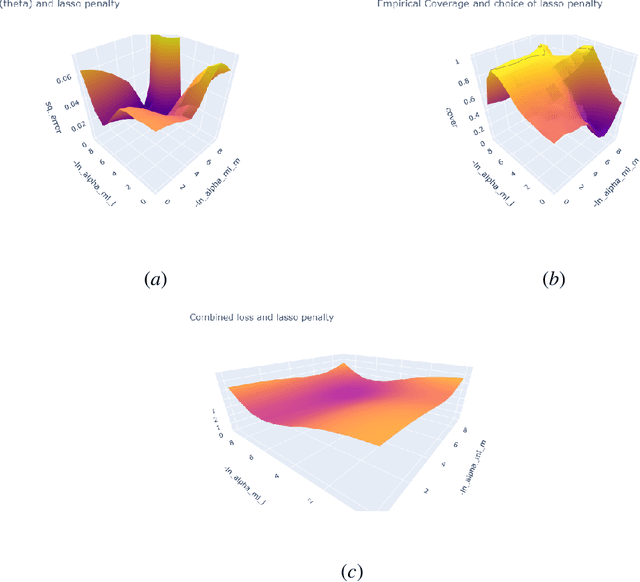

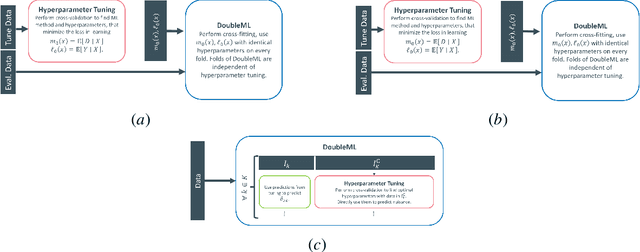
Abstract:Proper hyperparameter tuning is essential for achieving optimal performance of modern machine learning (ML) methods in predictive tasks. While there is an extensive literature on tuning ML learners for prediction, there is only little guidance available on tuning ML learners for causal machine learning and how to select among different ML learners. In this paper, we empirically assess the relationship between the predictive performance of ML methods and the resulting causal estimation based on the Double Machine Learning (DML) approach by Chernozhukov et al. (2018). DML relies on estimating so-called nuisance parameters by treating them as supervised learning problems and using them as plug-in estimates to solve for the (causal) parameter. We conduct an extensive simulation study using data from the 2019 Atlantic Causal Inference Conference Data Challenge. We provide empirical insights on the role of hyperparameter tuning and other practical decisions for causal estimation with DML. First, we assess the importance of data splitting schemes for tuning ML learners within Double Machine Learning. Second, we investigate how the choice of ML methods and hyperparameters, including recent AutoML frameworks, impacts the estimation performance for a causal parameter of interest. Third, we assess to what extent the choice of a particular causal model, as characterized by incorporated parametric assumptions, can be based on predictive performance metrics.
DoubleMLDeep: Estimation of Causal Effects with Multimodal Data
Feb 01, 2024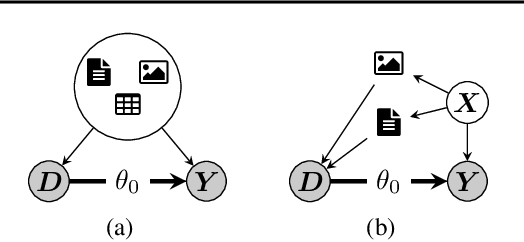
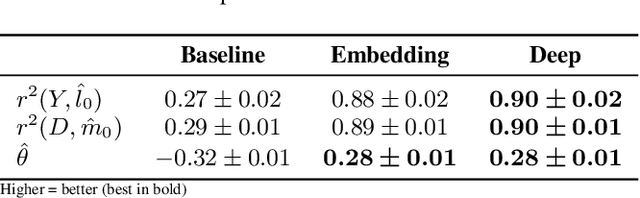
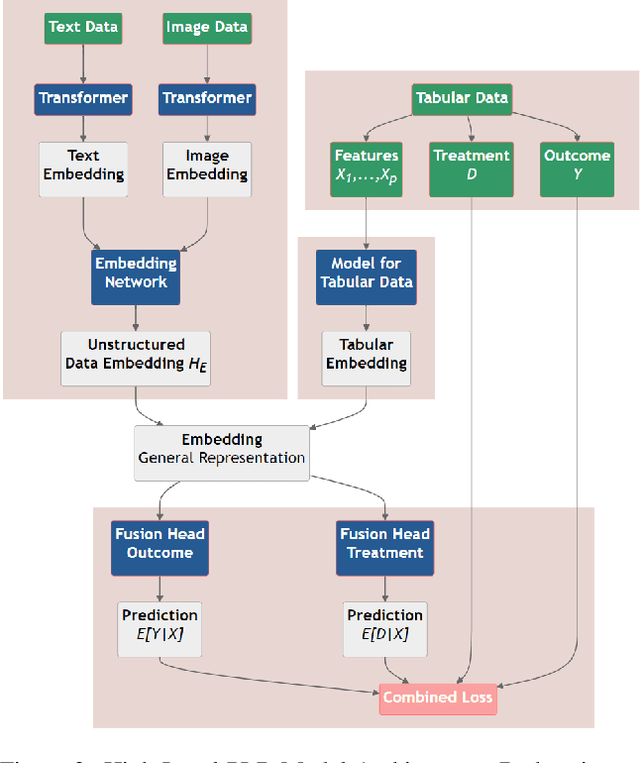
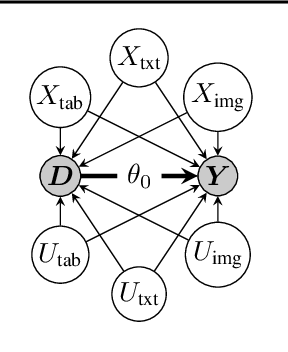
Abstract:This paper explores the use of unstructured, multimodal data, namely text and images, in causal inference and treatment effect estimation. We propose a neural network architecture that is adapted to the double machine learning (DML) framework, specifically the partially linear model. An additional contribution of our paper is a new method to generate a semi-synthetic dataset which can be used to evaluate the performance of causal effect estimation in the presence of text and images as confounders. The proposed methods and architectures are evaluated on the semi-synthetic dataset and compared to standard approaches, highlighting the potential benefit of using text and images directly in causal studies. Our findings have implications for researchers and practitioners in economics, marketing, finance, medicine and data science in general who are interested in estimating causal quantities using non-traditional data.
Hedonic Prices and Quality Adjusted Price Indices Powered by AI
Apr 28, 2023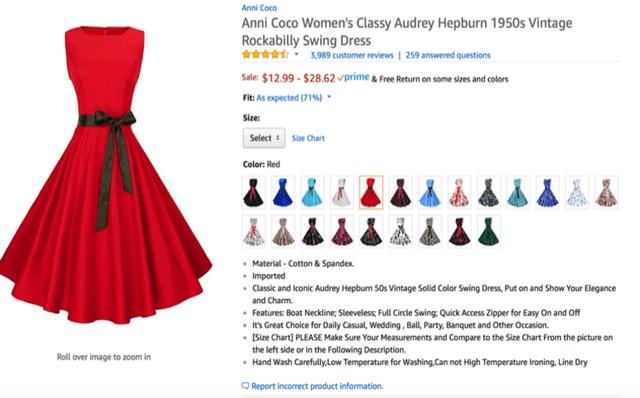
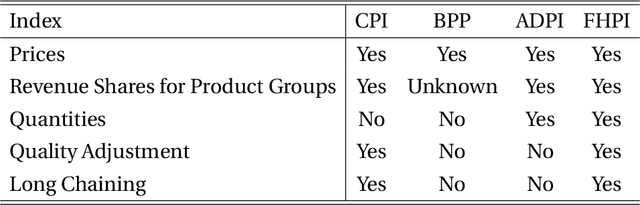
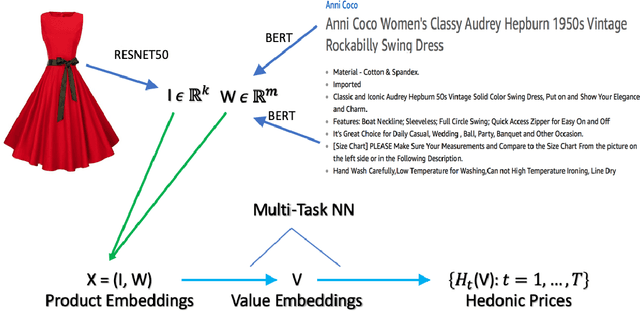

Abstract:Accurate, real-time measurements of price index changes using electronic records are essential for tracking inflation and productivity in today's economic environment. We develop empirical hedonic models that can process large amounts of unstructured product data (text, images, prices, quantities) and output accurate hedonic price estimates and derived indices. To accomplish this, we generate abstract product attributes, or ``features,'' from text descriptions and images using deep neural networks, and then use these attributes to estimate the hedonic price function. Specifically, we convert textual information about the product to numeric features using large language models based on transformers, trained or fine-tuned using product descriptions, and convert the product image to numeric features using a residual network model. To produce the estimated hedonic price function, we again use a multi-task neural network trained to predict a product's price in all time periods simultaneously. To demonstrate the performance of this approach, we apply the models to Amazon's data for first-party apparel sales and estimate hedonic prices. The resulting models have high predictive accuracy, with $R^2$ ranging from $80\%$ to $90\%$. Finally, we construct the AI-based hedonic Fisher price index, chained at the year-over-year frequency. We contrast the index with the CPI and other electronic indices.
Future-Dependent Value-Based Off-Policy Evaluation in POMDPs
Jul 26, 2022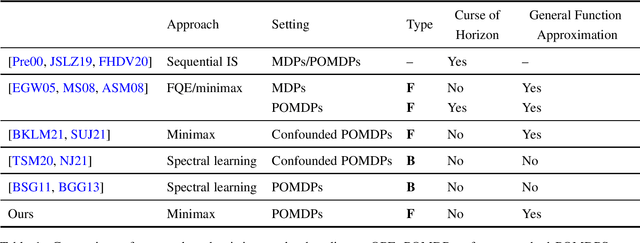
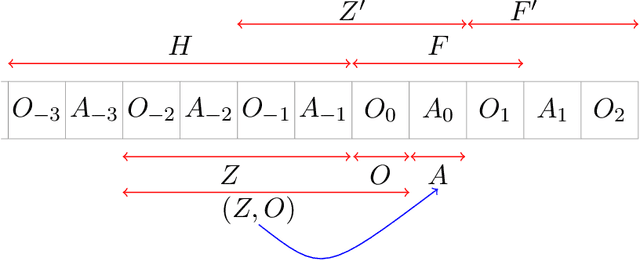
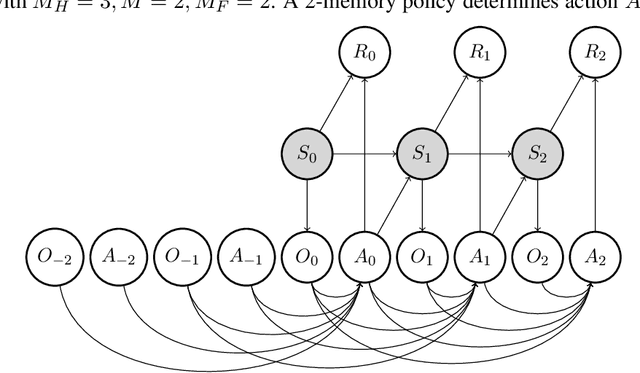
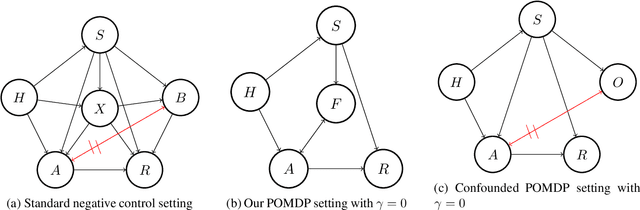
Abstract:We study off-policy evaluation (OPE) for partially observable MDPs (POMDPs) with general function approximation. Existing methods such as sequential importance sampling estimators and fitted-Q evaluation suffer from the curse of horizon in POMDPs. To circumvent this problem, we develop a novel model-free OPE method by introducing future-dependent value functions that take future proxies as inputs. Future-dependent value functions play similar roles as classical value functions in fully-observable MDPs. We derive a new Bellman equation for future-dependent value functions as conditional moment equations that use history proxies as instrumental variables. We further propose a minimax learning method to learn future-dependent value functions using the new Bellman equation. We obtain the PAC result, which implies our OPE estimator is consistent as long as futures and histories contain sufficient information about latent states, and the Bellman completeness. Finally, we extend our methods to learning of dynamics and establish the connection between our approach and the well-known spectral learning methods in POMDPs.
Automatic Debiased Machine Learning for Dynamic Treatment Effects
Apr 09, 2022

Abstract:We extend the idea of automated debiased machine learning to the dynamic treatment regime. We show that the multiply robust formula for the dynamic treatment regime with discrete treatments can be re-stated in terms of a recursive Riesz representer characterization of nested mean regressions. We then apply a recursive Riesz representer estimation learning algorithm that estimates de-biasing corrections without the need to characterize how the correction terms look like, such as for instance, products of inverse probability weighting terms, as is done in prior work on doubly robust estimation in the dynamic regime. Our approach defines a sequence of loss minimization problems, whose minimizers are the mulitpliers of the de-biasing correction, hence circumventing the need for solving auxiliary propensity models and directly optimizing for the mean squared error of the target de-biasing correction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge