Efficient and Sharp Off-Policy Evaluation in Robust Markov Decision Processes

We study evaluating a policy under best- and worst-case perturbations to a Markov decision process (MDP), given transition observations from the original MDP, whether under the same or different policy. This is an important problem when there is the possibility of a shift between historical and future environments, due to e.g. unmeasured confounding, distributional shift, or an adversarial environment. We propose a perturbation model that can modify transition kernel densities up to a given multiplicative factor or its reciprocal, which extends the classic marginal sensitivity model (MSM) for single time step decision making to infinite-horizon RL. We characterize the sharp bounds on policy value under this model, that is, the tightest possible bounds given by the transition observations from the original MDP, and we study the estimation of these bounds from such transition observations. We develop an estimator with several appealing guarantees: it is semiparametrically efficient, and remains so even when certain necessary nuisance functions such as worst-case Q-functions are estimated at slow nonparametric rates. It is also asymptotically normal, enabling easy statistical inference using Wald confidence intervals. In addition, when certain nuisances are estimated inconsistently we still estimate a valid, albeit possibly not sharp bounds on the policy value. We validate these properties in numeric simulations. The combination of accounting for environment shifts from train to test (robustness), being insensitive to nuisance-function estimation (orthogonality), and accounting for having only finite samples to learn from (inference) together leads to credible and reliable policy evaluation.

Low-Rank MDPs with Continuous Action Spaces

Low-Rank Markov Decision Processes (MDPs) have recently emerged as a promising framework within the domain of reinforcement learning (RL), as they allow for provably approximately correct (PAC) learning guarantees while also incorporating ML algorithms for representation learning. However, current methods for low-rank MDPs are limited in that they only consider finite action spaces, and give vacuous bounds as $|\mathcal{A}| \to \infty$, which greatly limits their applicability. In this work, we study the problem of extending such methods to settings with continuous actions, and explore multiple concrete approaches for performing this extension. As a case study, we consider the seminal FLAMBE algorithm (Agarwal et al., 2020), which is a reward-agnostic method for PAC RL with low-rank MDPs. We show that, without any modifications to the algorithm, we obtain similar PAC bound when actions are allowed to be continuous. Specifically, when the model for transition functions satisfies a Holder smoothness condition w.r.t. actions, and either the policy class has a uniformly bounded minimum density or the reward function is also Holder smooth, we obtain a polynomial PAC bound that depends on the order of smoothness.

Source Condition Double Robust Inference on Functionals of Inverse Problems

We consider estimation of parameters defined as linear functionals of solutions to linear inverse problems. Any such parameter admits a doubly robust representation that depends on the solution to a dual linear inverse problem, where the dual solution can be thought as a generalization of the inverse propensity function. We provide the first source condition double robust inference method that ensures asymptotic normality around the parameter of interest as long as either the primal or the dual inverse problem is sufficiently well-posed, without knowledge of which inverse problem is the more well-posed one. Our result is enabled by novel guarantees for iterated Tikhonov regularized adversarial estimators for linear inverse problems, over general hypothesis spaces, which are developments of independent interest.

Minimax Instrumental Variable Regression and $L_2$ Convergence Guarantees without Identification or Closedness

In this paper, we study nonparametric estimation of instrumental variable (IV) regressions. Recently, many flexible machine learning methods have been developed for instrumental variable estimation. However, these methods have at least one of the following limitations: (1) restricting the IV regression to be uniquely identified; (2) only obtaining estimation error rates in terms of pseudometrics (\emph{e.g.,} projected norm) rather than valid metrics (\emph{e.g.,} $L_2$ norm); or (3) imposing the so-called closedness condition that requires a certain conditional expectation operator to be sufficiently smooth. In this paper, we present the first method and analysis that can avoid all three limitations, while still permitting general function approximation. Specifically, we propose a new penalized minimax estimator that can converge to a fixed IV solution even when there are multiple solutions, and we derive a strong $L_2$ error rate for our estimator under lax conditions. Notably, this guarantee only needs a widely-used source condition and realizability assumptions, but not the so-called closedness condition. We argue that the source condition and the closedness condition are inherently conflicting, so relaxing the latter significantly improves upon the existing literature that requires both conditions. Our estimator can achieve this improvement because it builds on a novel formulation of the IV estimation problem as a constrained optimization problem.

Provable Safe Reinforcement Learning with Binary Feedback

Safety is a crucial necessity in many applications of reinforcement learning (RL), whether robotic, automotive, or medical. Many existing approaches to safe RL rely on receiving numeric safety feedback, but in many cases this feedback can only take binary values; that is, whether an action in a given state is safe or unsafe. This is particularly true when feedback comes from human experts. We therefore consider the problem of provable safe RL when given access to an offline oracle providing binary feedback on the safety of state, action pairs. We provide a novel meta algorithm, SABRE, which can be applied to any MDP setting given access to a blackbox PAC RL algorithm for that setting. SABRE applies concepts from active learning to reinforcement learning to provably control the number of queries to the safety oracle. SABRE works by iteratively exploring the state space to find regions where the agent is currently uncertain about safety. Our main theoretical results shows that, under appropriate technical assumptions, SABRE never takes unsafe actions during training, and is guaranteed to return a near-optimal safe policy with high probability. We provide a discussion of how our meta-algorithm may be applied to various settings studied in both theoretical and empirical frameworks.

Future-Dependent Value-Based Off-Policy Evaluation in POMDPs

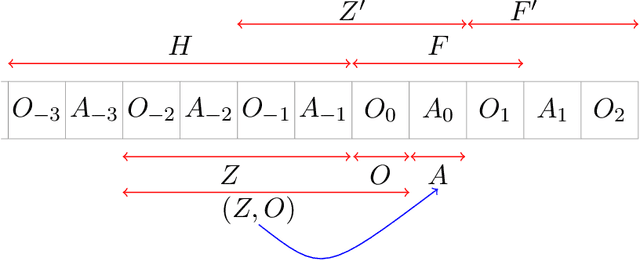
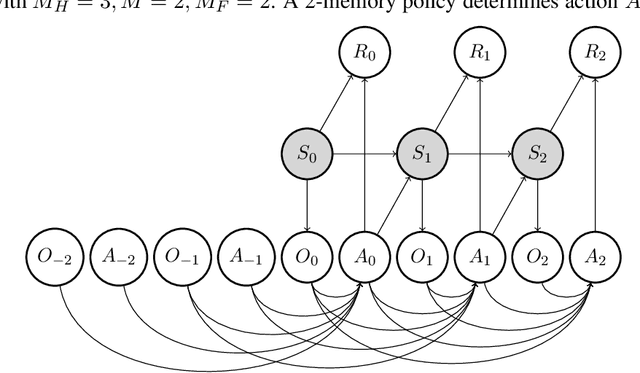
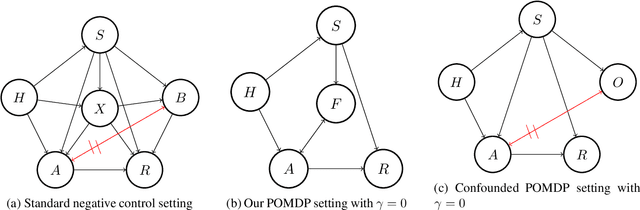
We study off-policy evaluation (OPE) for partially observable MDPs (POMDPs) with general function approximation. Existing methods such as sequential importance sampling estimators and fitted-Q evaluation suffer from the curse of horizon in POMDPs. To circumvent this problem, we develop a novel model-free OPE method by introducing future-dependent value functions that take future proxies as inputs. Future-dependent value functions play similar roles as classical value functions in fully-observable MDPs. We derive a new Bellman equation for future-dependent value functions as conditional moment equations that use history proxies as instrumental variables. We further propose a minimax learning method to learn future-dependent value functions using the new Bellman equation. We obtain the PAC result, which implies our OPE estimator is consistent as long as futures and histories contain sufficient information about latent states, and the Bellman completeness. Finally, we extend our methods to learning of dynamics and establish the connection between our approach and the well-known spectral learning methods in POMDPs.

Proximal Reinforcement Learning: Efficient Off-Policy Evaluation in Partially Observed Markov Decision Processes

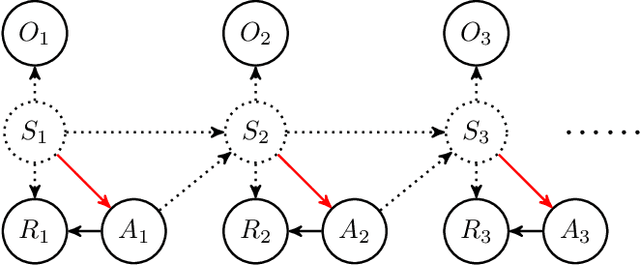
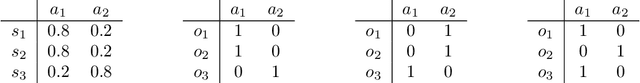
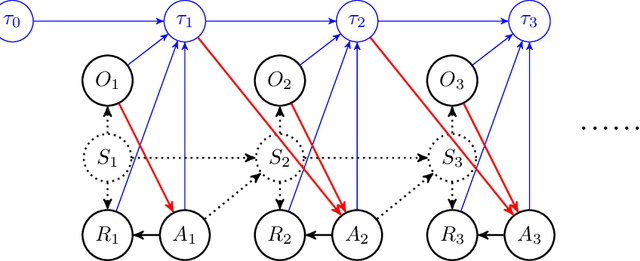
In applications of offline reinforcement learning to observational data, such as in healthcare or education, a general concern is that observed actions might be affected by unobserved factors, inducing confounding and biasing estimates derived under the assumption of a perfect Markov decision process (MDP) model. Here we tackle this by considering off-policy evaluation in a partially observed MDP (POMDP). Specifically, we consider estimating the value of a given target policy in a POMDP given trajectories with only partial state observations generated by a different and unknown policy that may depend on the unobserved state. We tackle two questions: what conditions allow us to identify the target policy value from the observed data and, given identification, how to best estimate it. To answer these, we extend the framework of proximal causal inference to our POMDP setting, providing a variety of settings where identification is made possible by the existence of so-called bridge functions. We then show how to construct semiparametrically efficient estimators in these settings. We term the resulting framework proximal reinforcement learning (PRL). We demonstrate the benefits of PRL in an extensive simulation study.

Have you tried Neural Topic Models? Comparative Analysis of Neural and Non-Neural Topic Models with Application to COVID-19 Twitter Data

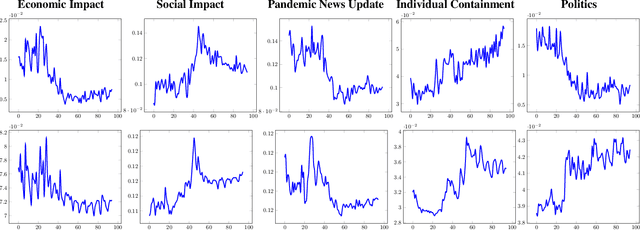
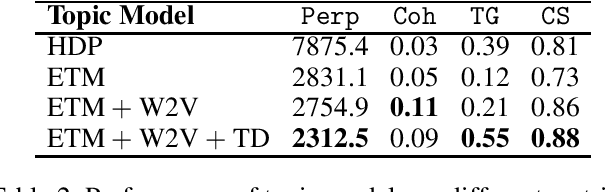
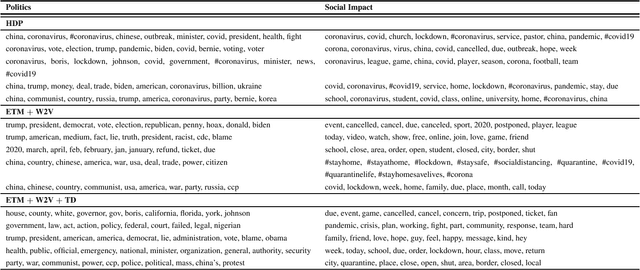
Topic models are widely used in studying social phenomena. We conduct a comparative study examining state-of-the-art neural versus non-neural topic models, performing a rigorous quantitative and qualitative assessment on a dataset of tweets about the COVID-19 pandemic. Our results show that not only do neural topic models outperform their classical counterparts on standard evaluation metrics, but they also produce more coherent topics, which are of great benefit when studying complex social problems. We also propose a novel regularization term for neural topic models, which is designed to address the well-documented problem of mode collapse, and demonstrate its effectiveness.

The Variational Method of Moments

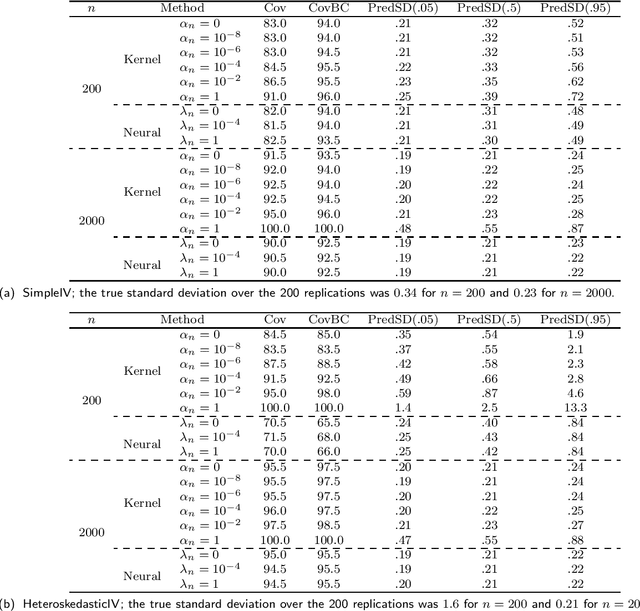
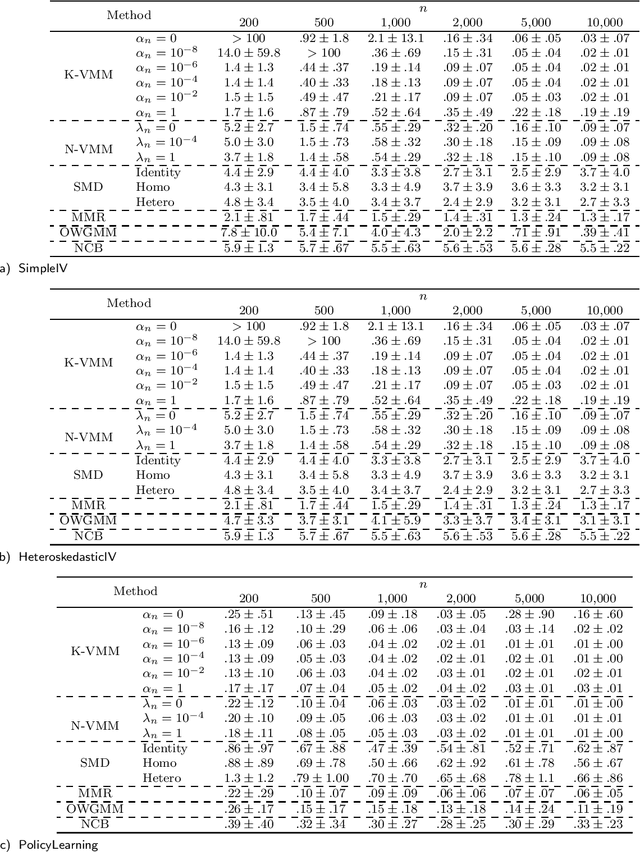
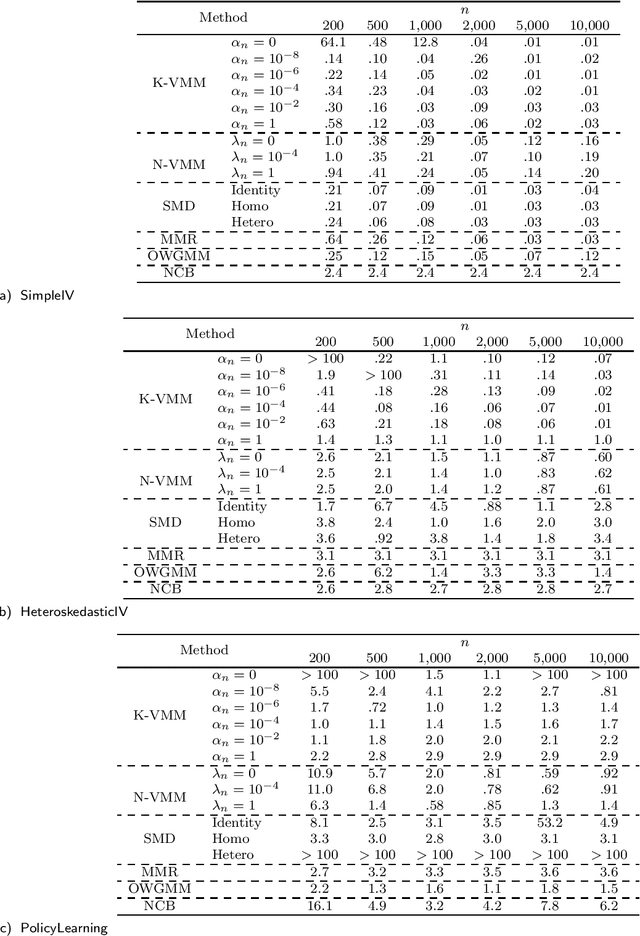
The conditional moment problem is a powerful formulation for describing structural causal parameters in terms of observables, a prominent example being instrumental variable regression. A standard approach is to reduce the problem to a finite set of marginal moment conditions and apply the optimally weighted generalized method of moments (OWGMM), but this requires we know a finite set of identifying moments, can still be inefficient even if identifying, or can be unwieldy and impractical if we use a growing sieve of moments. Motivated by a variational minimax reformulation of OWGMM, we define a very general class of estimators for the conditional moment problem, which we term the variational method of moments (VMM) and which naturally enables controlling infinitely-many moments. We provide a detailed theoretical analysis of multiple VMM estimators, including based on kernel methods and neural networks, and provide appropriate conditions under which these estimators are consistent, asymptotically normal, and semiparametrically efficient in the full conditional moment model. This is in contrast to other recently proposed methods for solving conditional moment problems based on adversarial machine learning, which do not incorporate optimal weighting, do not establish asymptotic normality, and are not semiparametrically efficient.

Off-policy Evaluation in Infinite-Horizon Reinforcement Learning with Latent Confounders

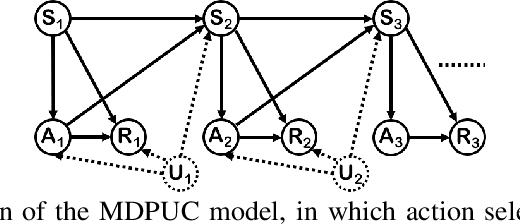
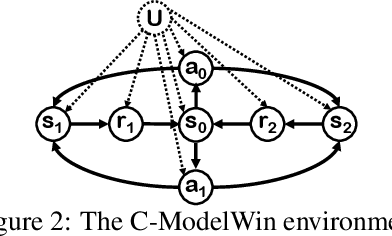
Off-policy evaluation (OPE) in reinforcement learning is an important problem in settings where experimentation is limited, such as education and healthcare. But, in these very same settings, observed actions are often confounded by unobserved variables making OPE even more difficult. We study an OPE problem in an infinite-horizon, ergodic Markov decision process with unobserved confounders, where states and actions can act as proxies for the unobserved confounders. We show how, given only a latent variable model for states and actions, policy value can be identified from off-policy data. Our method involves two stages. In the first, we show how to use proxies to estimate stationary distribution ratios, extending recent work on breaking the curse of horizon to the confounded setting. In the second, we show optimal balancing can be combined with such learned ratios to obtain policy value while avoiding direct modeling of reward functions. We establish theoretical guarantees of consistency, and benchmark our method empirically.