Off-policy Evaluation in Infinite-Horizon Reinforcement Learning with Latent Confounders
Paper and Code
Jul 27, 2020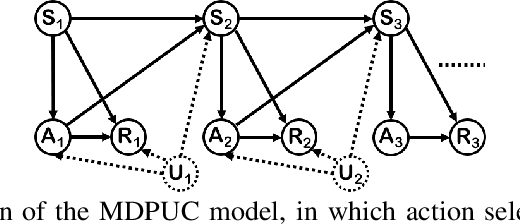
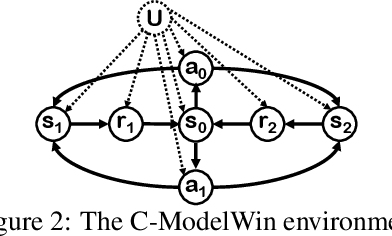

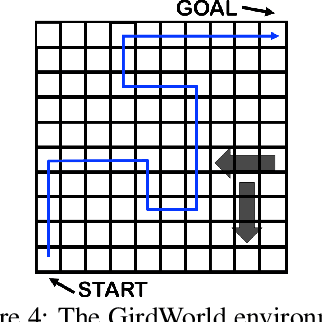
Off-policy evaluation (OPE) in reinforcement learning is an important problem in settings where experimentation is limited, such as education and healthcare. But, in these very same settings, observed actions are often confounded by unobserved variables making OPE even more difficult. We study an OPE problem in an infinite-horizon, ergodic Markov decision process with unobserved confounders, where states and actions can act as proxies for the unobserved confounders. We show how, given only a latent variable model for states and actions, policy value can be identified from off-policy data. Our method involves two stages. In the first, we show how to use proxies to estimate stationary distribution ratios, extending recent work on breaking the curse of horizon to the confounded setting. In the second, we show optimal balancing can be combined with such learned ratios to obtain policy value while avoiding direct modeling of reward functions. We establish theoretical guarantees of consistency, and benchmark our method empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge