Adventures in Demand Analysis Using AI

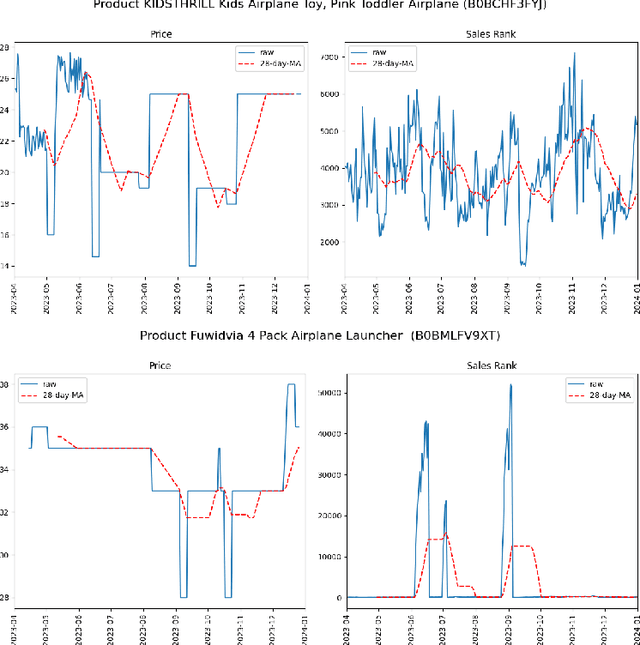
This paper advances empirical demand analysis by integrating multimodal product representations derived from artificial intelligence (AI). Using a detailed dataset of toy cars on \textit{Amazon.com}, we combine text descriptions, images, and tabular covariates to represent each product using transformer-based embedding models. These embeddings capture nuanced attributes, such as quality, branding, and visual characteristics, that traditional methods often struggle to summarize. Moreover, we fine-tune these embeddings for causal inference tasks. We show that the resulting embeddings substantially improve the predictive accuracy of sales ranks and prices and that they lead to more credible causal estimates of price elasticity. Notably, we uncover strong heterogeneity in price elasticity driven by these product-specific features. Our findings illustrate that AI-driven representations can enrich and modernize empirical demand analysis. The insights generated may also prove valuable for applied causal inference more broadly.

DoubleMLDeep: Estimation of Causal Effects with Multimodal Data

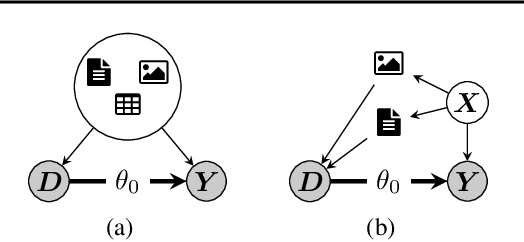
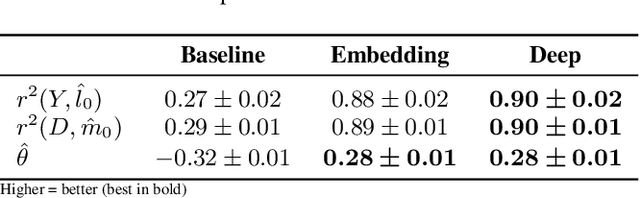
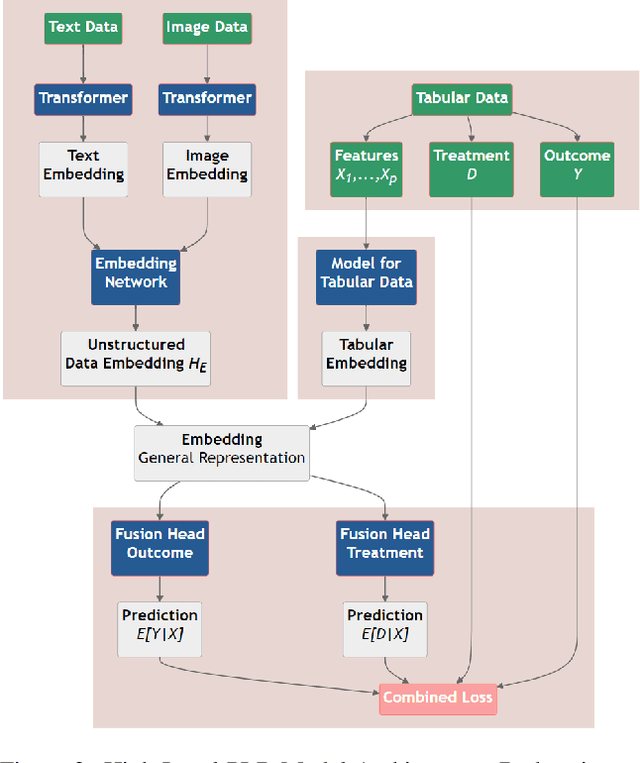
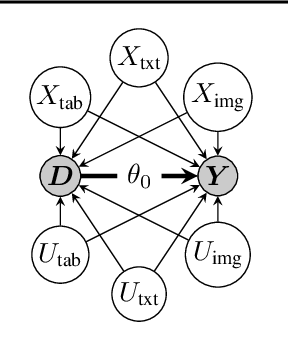
This paper explores the use of unstructured, multimodal data, namely text and images, in causal inference and treatment effect estimation. We propose a neural network architecture that is adapted to the double machine learning (DML) framework, specifically the partially linear model. An additional contribution of our paper is a new method to generate a semi-synthetic dataset which can be used to evaluate the performance of causal effect estimation in the presence of text and images as confounders. The proposed methods and architectures are evaluated on the semi-synthetic dataset and compared to standard approaches, highlighting the potential benefit of using text and images directly in causal studies. Our findings have implications for researchers and practitioners in economics, marketing, finance, medicine and data science in general who are interested in estimating causal quantities using non-traditional data.

Hedonic Prices and Quality Adjusted Price Indices Powered by AI

Accurate, real-time measurements of price index changes using electronic records are essential for tracking inflation and productivity in today's economic environment. We develop empirical hedonic models that can process large amounts of unstructured product data (text, images, prices, quantities) and output accurate hedonic price estimates and derived indices. To accomplish this, we generate abstract product attributes, or ``features,'' from text descriptions and images using deep neural networks, and then use these attributes to estimate the hedonic price function. Specifically, we convert textual information about the product to numeric features using large language models based on transformers, trained or fine-tuned using product descriptions, and convert the product image to numeric features using a residual network model. To produce the estimated hedonic price function, we again use a multi-task neural network trained to predict a product's price in all time periods simultaneously. To demonstrate the performance of this approach, we apply the models to Amazon's data for first-party apparel sales and estimate hedonic prices. The resulting models have high predictive accuracy, with $R^2$ ranging from $80\%$ to $90\%$. Finally, we construct the AI-based hedonic Fisher price index, chained at the year-over-year frequency. We contrast the index with the CPI and other electronic indices.

Synthetic Combinations: A Causal Inference Framework for Combinatorial Interventions

We consider a setting with $N$ heterogeneous units and $p$ interventions. Our goal is to learn unit-specific potential outcomes for any combination of these $p$ interventions, i.e., $N \times 2^p$ causal parameters. Choosing combinations of interventions is a problem that naturally arises in many applications such as factorial design experiments, recommendation engines (e.g., showing a set of movies that maximizes engagement for users), combination therapies in medicine, selecting important features for ML models, etc. Running $N \times 2^p$ experiments to estimate the various parameters is infeasible as $N$ and $p$ grow. Further, with observational data there is likely confounding, i.e., whether or not a unit is seen under a combination is correlated with its potential outcome under that combination. To address these challenges, we propose a novel model that imposes latent structure across both units and combinations. We assume latent similarity across units (i.e., the potential outcomes matrix is rank $r$) and regularity in how combinations interact (i.e., the coefficients in the Fourier expansion of the potential outcomes is $s$ sparse). We establish identification for all causal parameters despite unobserved confounding. We propose an estimation procedure, Synthetic Combinations, and establish finite-sample consistency under precise conditions on the observation pattern. Our results imply Synthetic Combinations consistently estimates unit-specific potential outcomes given $\text{poly}(r) \times (N + s^2p)$ observations. In comparison, previous methods that do not exploit structure across both units and combinations have sample complexity scaling as $\min(N \times s^2p, \ \ r \times (N + 2^p))$. We use Synthetic Combinations to propose a data-efficient experimental design mechanism for combinatorial causal inference. We corroborate our theoretical findings with numerical simulations.

Kernel Ridge Regression Inference

We provide uniform confidence bands for kernel ridge regression (KRR), with finite sample guarantees. KRR is ubiquitous, yet--to our knowledge--this paper supplies the first exact, uniform confidence bands for KRR in the non-parametric regime where the regularization parameter $\lambda$ converges to 0, for general data distributions. Our proposed uniform confidence band is based on a new, symmetrized multiplier bootstrap procedure with a closed form solution, which allows for valid uncertainty quantification without assumptions on the bias. To justify the procedure, we derive non-asymptotic, uniform Gaussian and bootstrap couplings for partial sums in a reproducing kernel Hilbert space (RKHS) with bounded kernel. Our results imply strong approximation for empirical processes indexed by the RKHS unit ball, with sharp, logarithmic dependence on the covering number.

Frank Wolfe Meets Metric Entropy

The Frank-Wolfe algorithm has seen a resurgence in popularity due to its ability to efficiently solve constrained optimization problems in machine learning and high-dimensional statistics. As such, there is much interest in establishing when the algorithm may possess a "linear" $O(\log(1/\epsilon))$ dimension-free iteration complexity comparable to projected gradient descent. In this paper, we provide a general technique for establishing domain specific and easy-to-estimate lower bounds for Frank-Wolfe and its variants using the metric entropy of the domain. Most notably, we show that a dimension-free linear upper bound must fail not only in the worst case, but in the \emph{average case}: for a Gaussian or spherical random polytope in $\mathbb{R}^d$ with $\mathrm{poly}(d)$ vertices, Frank-Wolfe requires up to $\tilde\Omega(d)$ iterations to achieve a $O(1/d)$ error bound, with high probability. We also establish this phenomenon for the nuclear norm ball. The link with metric entropy also has interesting positive implications for conditional gradient algorithms in statistics, such as gradient boosting and matching pursuit. In particular, we show that it is possible to extract fast-decaying upper bounds on the excess risk directly from an analysis of the underlying optimization procedure.

Classification as Direction Recovery: Improved Guarantees via Scale Invariance

Modern algorithms for binary classification rely on an intermediate regression problem for computational tractability. In this paper, we establish a geometric distinction between classification and regression that allows risk in these two settings to be more precisely related. In particular, we note that classification risk depends only on the direction of the regressor, and we take advantage of this scale invariance to improve existing guarantees for how classification risk is bounded by the risk in the intermediate regression problem. Building on these guarantees, our analysis makes it possible to compare algorithms more accurately against each other and suggests viewing classification as unique from regression rather than a byproduct of it. While regression aims to converge toward the conditional expectation function in location, we propose that classification should instead aim to recover its direction.

Localization, Convexity, and Star Aggregation

Offset Rademacher complexities have been shown to imply sharp, data-dependent upper bounds for the square loss in a broad class of problems including improper statistical learning and online learning. We show that in the statistical setting, the offset complexity upper bound can be generalized to any loss satisfying a certain uniform convexity condition. Amazingly, this condition is shown to also capture exponential concavity and self-concordance, uniting several apparently disparate results. By a unified geometric argument, these bounds translate directly to improper learning in a non-convex class using Audibert's "star algorithm." As applications, we recover the optimal rates for proper and improper learning with the $p$-loss, $1 < p < \infty$, closing the gap for $p > 2$, and show that improper variants of empirical risk minimization can attain fast rates for logistic regression and other generalized linear models.

A Resolution in Algorithmic Fairness: Calibrated Scores for Fair Classifications

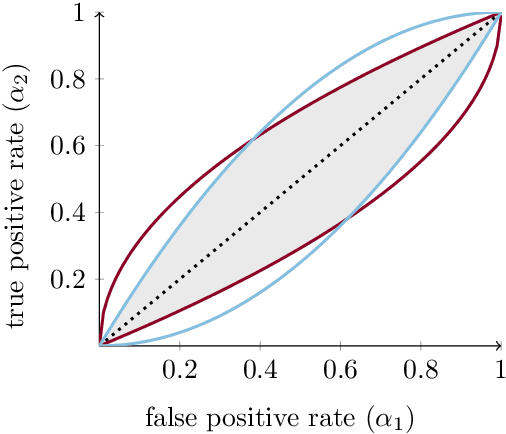
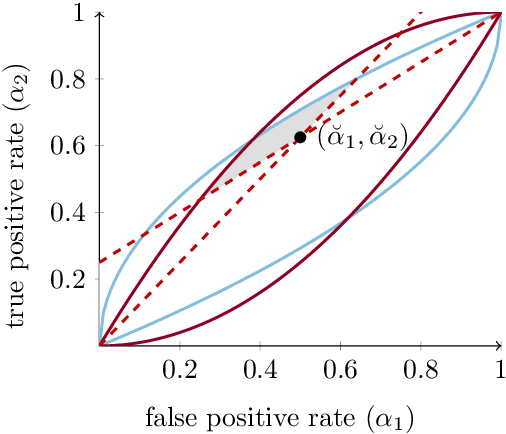
Calibration and equal error rates are fundamental conditions for algorithmic fairness that have been shown to conflict with each other, suggesting that they cannot be satisfied simultaneously. This paper shows that the two are in fact compatible and presents a method for reconciling them. In particular, we derive necessary and sufficient conditions for the existence of calibrated scores that yield classifications achieving equal error rates. We then present an algorithm that searches for the most informative score subject to both calibration and minimal error rate disparity. Applied empirically to credit lending, our algorithm provides a solution that is more fair and profitable than a common alternative that omits sensitive features.