Classification as Direction Recovery: Improved Guarantees via Scale Invariance

Modern algorithms for binary classification rely on an intermediate regression problem for computational tractability. In this paper, we establish a geometric distinction between classification and regression that allows risk in these two settings to be more precisely related. In particular, we note that classification risk depends only on the direction of the regressor, and we take advantage of this scale invariance to improve existing guarantees for how classification risk is bounded by the risk in the intermediate regression problem. Building on these guarantees, our analysis makes it possible to compare algorithms more accurately against each other and suggests viewing classification as unique from regression rather than a byproduct of it. While regression aims to converge toward the conditional expectation function in location, we propose that classification should instead aim to recover its direction.

Resolving the Disparate Impact of Uncertainty: Affirmative Action vs. Affirmative Information

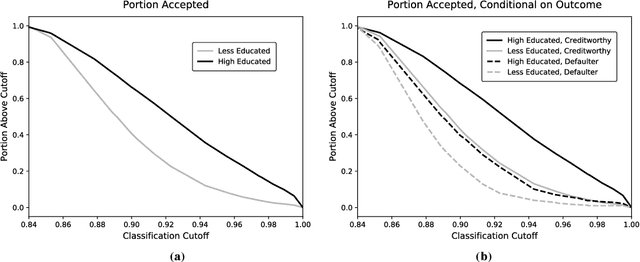
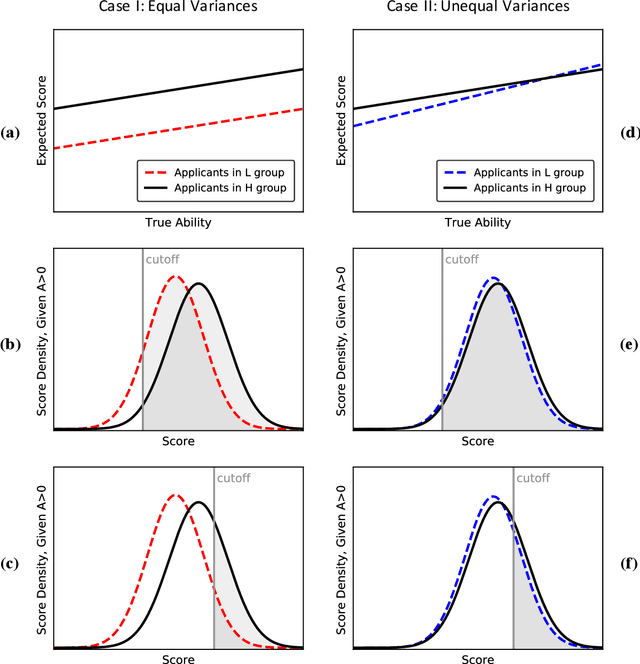
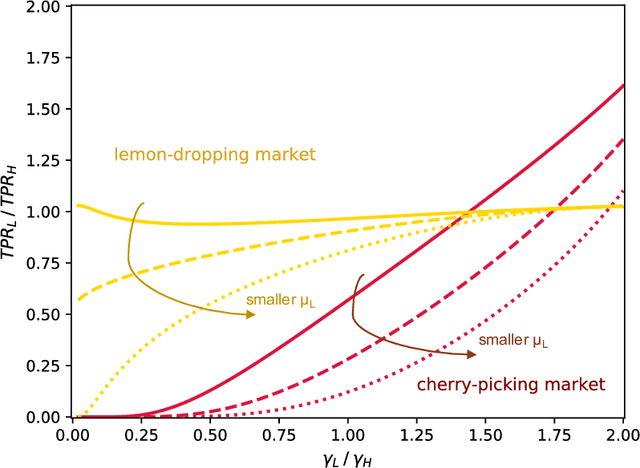
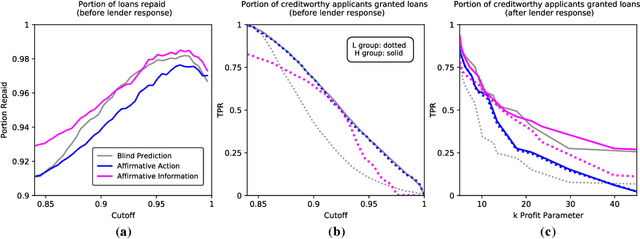
Algorithmic risk assessments hold the promise of greatly advancing accurate decision-making, but in practice, multiple real-world examples have been shown to distribute errors disproportionately across demographic groups. In this paper, we characterize why error disparities arise in the first place. We show that predictive uncertainty often leads classifiers to systematically disadvantage groups with lower-mean outcomes, assigning them smaller true and false positive rates than their higher-mean counterparts. This can occur even when prediction is group-blind. We prove that to avoid these error imbalances, individuals in lower-mean groups must either be over-represented among positive classifications or be assigned more accurate predictions than those in higher-mean groups. We focus on the latter condition as a solution to bridge error rate divides and show that data acquisition for low-mean groups can increase access to opportunity. We call the strategy "affirmative information" and compare it to traditional affirmative action in the classification task of identifying creditworthy borrowers.