Self-reinforced polynomial approximation methods for concentrated probability densities

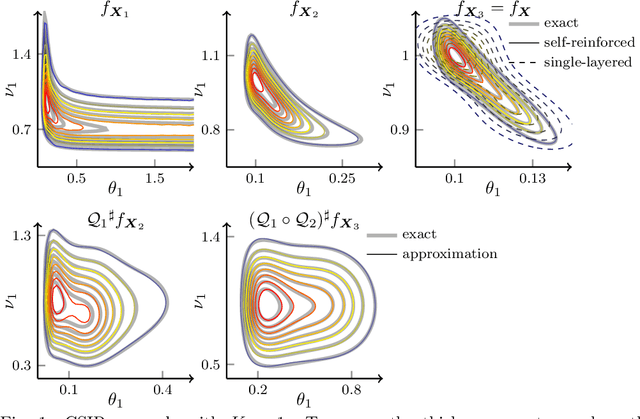
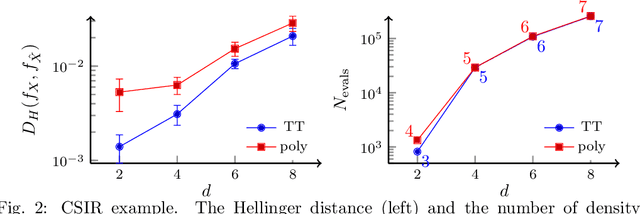
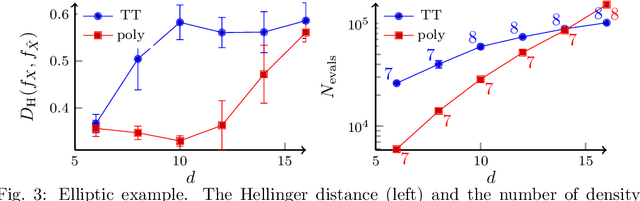
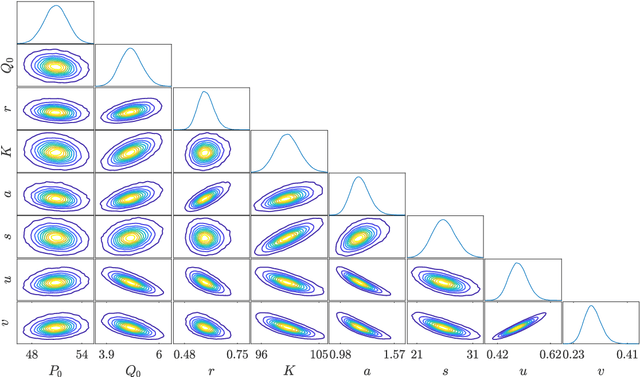
Transport map methods offer a powerful statistical learning tool that can couple a target high-dimensional random variable with some reference random variable using invertible transformations. This paper presents new computational techniques for building the Knothe--Rosenblatt (KR) rearrangement based on general separable functions. We first introduce a new construction of the KR rearrangement -- with guaranteed invertibility in its numerical implementation -- based on approximating the density of the target random variable using tensor-product spectral polynomials and downward closed sparse index sets. Compared to other constructions of KR arrangements based on either multi-linear approximations or nonlinear optimizations, our new construction only relies on a weighted least square approximation procedure. Then, inspired by the recently developed deep tensor trains (Cui and Dolgov, Found. Comput. Math. 22:1863--1922, 2022), we enhance the approximation power of sparse polynomials by preconditioning the density approximation problem using compositions of maps. This is particularly suitable for high-dimensional and concentrated probability densities commonly seen in many applications. We approximate the complicated target density by a composition of self-reinforced KR rearrangements, in which previously constructed KR rearrangements -- based on the same approximation ansatz -- are used to precondition the density approximation problem for building each new KR rearrangement. We demonstrate the efficiency of our proposed methods and the importance of using the composite map on several inverse problems governed by ordinary differential equations (ODEs) and partial differential equations (PDEs).

A weighted subspace exponential kernel for support tensor machines

High-dimensional data in the form of tensors are challenging for kernel classification methods. To both reduce the computational complexity and extract informative features, kernels based on low-rank tensor decompositions have been proposed. However, what decisive features of the tensors are exploited by these kernels is often unclear. In this paper we propose a novel kernel that is based on the Tucker decomposition. For this kernel the Tucker factors are computed based on re-weighting of the Tucker matrices with tuneable powers of singular values from the HOSVD decomposition. This provides a mechanism to balance the contribution of the Tucker core and factors of the data. We benchmark support tensor machines with this new kernel on several datasets. First we generate synthetic data where two classes differ in either Tucker factors or core, and compare our novel and previously existing kernels. We show robustness of the new kernel with respect to both classification scenarios. We further test the new method on real-world datasets. The proposed kernel has demonstrated a higher test accuracy than the state-of-the-art tensor train multi-way multi-level kernel, and a significantly lower computational time.

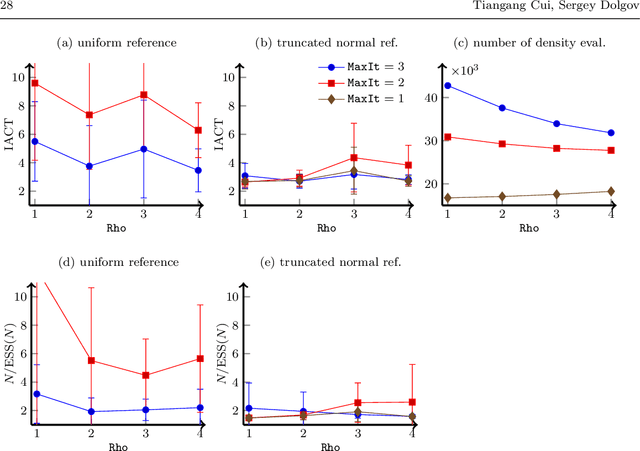
Deep importance sampling using tensor-trains with application to a priori and a posteriori rare event estimation

We propose a deep importance sampling method that is suitable for estimating rare event probabilities in high-dimensional problems. We approximate the optimal importance distribution in a general importance sampling problem as the pushforward of a reference distribution under a composition of order-preserving transformations, in which each transformation is formed by a squared tensor-train decomposition. The squared tensor-train decomposition provides a scalable ansatz for building order-preserving high-dimensional transformations via density approximations. The use of composition of maps moving along a sequence of bridging densities alleviates the difficulty of directly approximating concentrated density functions. To compute expectations over unnormalized probability distributions, we design a ratio estimator that estimates the normalizing constant using a separate importance distribution, again constructed via a composition of transformations in tensor-train format. This offers better theoretical variance reduction compared with self-normalized importance sampling, and thus opens the door to efficient computation of rare event probabilities in Bayesian inference problems. Numerical experiments on problems constrained by differential equations show little to no increase in the computational complexity with the event probability going to zero, and allow to compute hitherto unattainable estimates of rare event probabilities for complex, high-dimensional posterior densities.

Conditional Deep Inverse Rosenblatt Transports

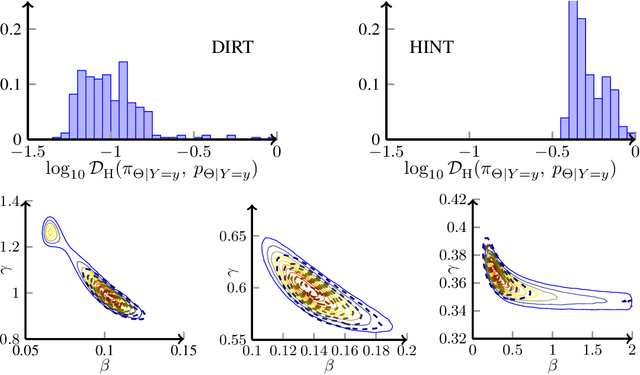
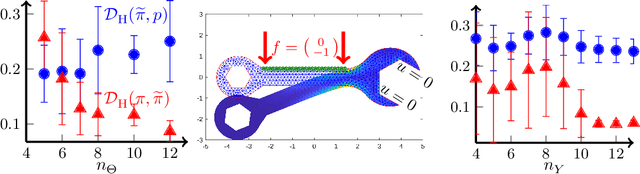
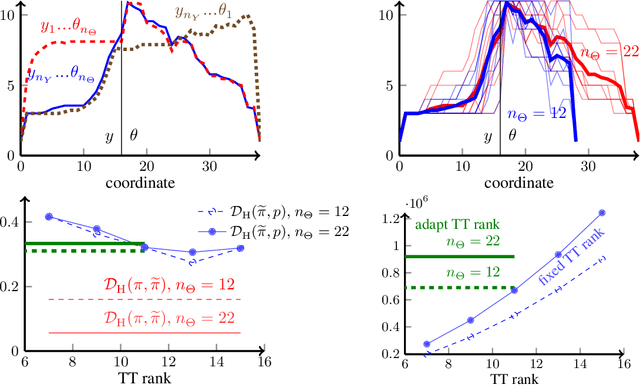
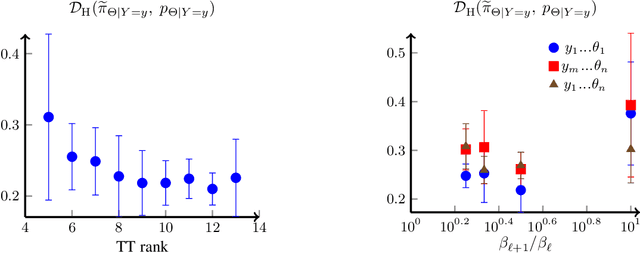
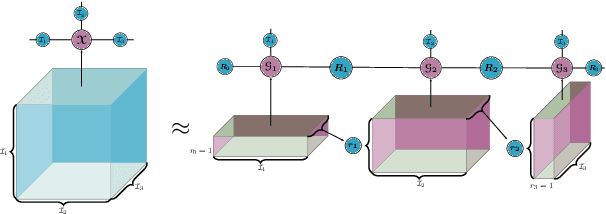
We present a novel offline-online method to mitigate the computational burden of the characterization of conditional beliefs in statistical learning. In the offline phase, the proposed method learns the joint law of the belief random variables and the observational random variables in the tensor-train (TT) format. In the online phase, it utilizes the resulting order-preserving conditional transport map to issue real-time characterization of the conditional beliefs given new observed information. Compared with the state-of-the-art normalizing flows techniques, the proposed method relies on function approximation and is equipped with thorough performance analysis. This also allows us to further extend the capability of transport maps in challenging problems with high-dimensional observations and high-dimensional belief variables. On the one hand, we present novel heuristics to reorder and/or reparametrize the variables to enhance the approximation power of TT. On the other, we integrate the TT-based transport maps and the parameter reordering/reparametrization into layered compositions to further improve the performance of the resulting transport maps. We demonstrate the efficiency of the proposed method on various statistical learning tasks in ordinary differential equations (ODEs) and partial differential equations (PDEs).

Deep Composition of Tensor Trains using Squared Inverse Rosenblatt Transports

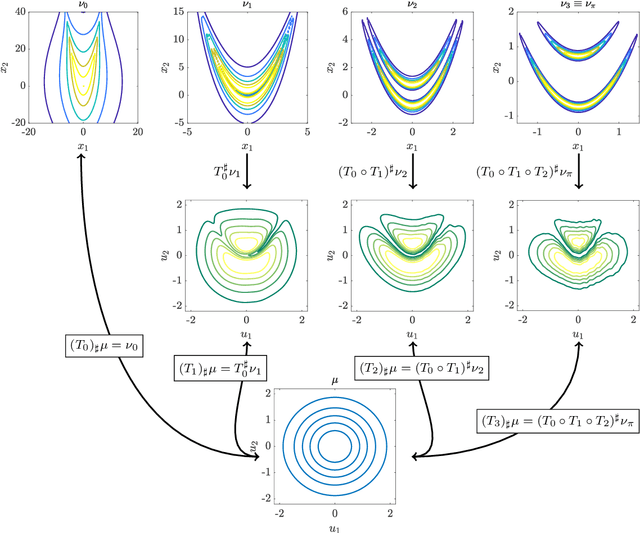
Characterising intractable high-dimensional random variables is one of the fundamental challenges in stochastic computation. The recent surge of transport maps offers a mathematical foundation and new insights for tackling this challenge by coupling intractable random variables with tractable reference random variables. This paper generalises a recently developed functional tensor-train (FTT) approximation of the inverse Rosenblatt transport [14] to a wide class of high-dimensional nonnegative functions, such as unnormalised probability density functions. First, we extend the inverse Rosenblatt transform to enable the transport to general reference measures other than the uniform measure. We develop an efficient procedure to compute this transport from a squared FTT decomposition which preserves the monotonicity. More crucially, we integrate the proposed monotonicity-preserving FTT transport into a nested variable transformation framework inspired by deep neural networks. The resulting deep inverse Rosenblatt transport significantly expands the capability of tensor approximations and transport maps to random variables with complicated nonlinear interactions and concentrated density functions. We demonstrate the efficacy of the proposed approach on a range of applications in statistical learning and uncertainty quantification, including parameter estimation for dynamical systems and inverse problems constrained by partial differential equations.

Efficient Structure-preserving Support Tensor Train Machine

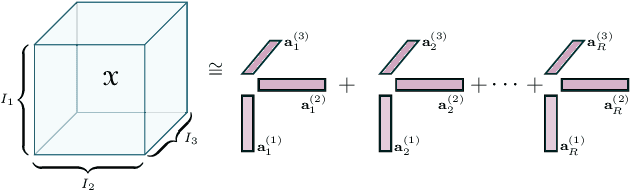
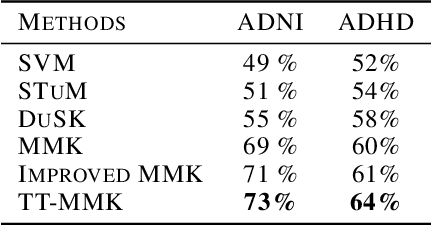
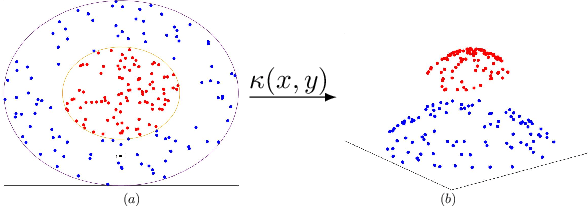
Deploying the multi-relational tensor structure of a high dimensional feature space, more efficiently improves the performance of machine learning algorithms. One encounters the \emph{curse of dimensionality}, and working with vectorized data fails to preserve the data structure. To mitigate the nonlinear relationship of tensor data more economically, we propose the \emph{Tensor Train Multi-way Multi-level Kernel (TT-MMK)}. This technique combines kernel filtering of the initial input data (\emph{Kernelized Tensor Train (KTT)}), stable reparametrization of the KTT in the Canonical Polyadic (CP) format, and the Dual Structure-preserving Support Vector Machine (\emph{SVM}) Kernel for revealing nonlinear relationships. We demonstrate numerically that the TT-MMK method is more reliable computationally, is less sensitive to tuning parameters, and gives higher prediction accuracy in the SVM classification compared to similar tensorised SVM methods.