A weighted subspace exponential kernel for support tensor machines

High-dimensional data in the form of tensors are challenging for kernel classification methods. To both reduce the computational complexity and extract informative features, kernels based on low-rank tensor decompositions have been proposed. However, what decisive features of the tensors are exploited by these kernels is often unclear. In this paper we propose a novel kernel that is based on the Tucker decomposition. For this kernel the Tucker factors are computed based on re-weighting of the Tucker matrices with tuneable powers of singular values from the HOSVD decomposition. This provides a mechanism to balance the contribution of the Tucker core and factors of the data. We benchmark support tensor machines with this new kernel on several datasets. First we generate synthetic data where two classes differ in either Tucker factors or core, and compare our novel and previously existing kernels. We show robustness of the new kernel with respect to both classification scenarios. We further test the new method on real-world datasets. The proposed kernel has demonstrated a higher test accuracy than the state-of-the-art tensor train multi-way multi-level kernel, and a significantly lower computational time.

Efficient Structure-preserving Support Tensor Train Machine

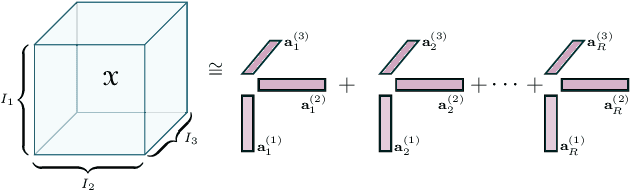
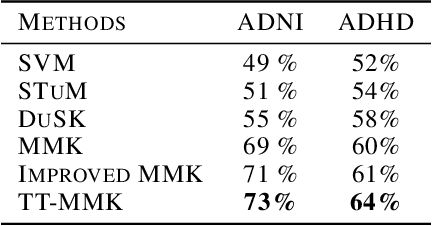
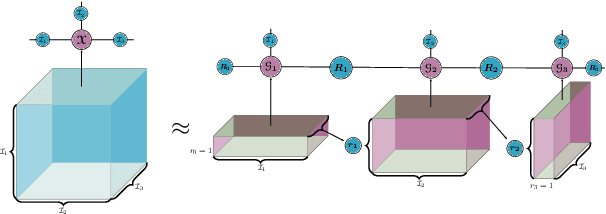
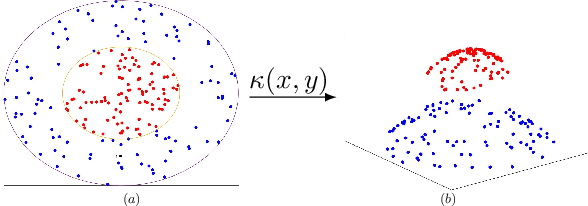
Deploying the multi-relational tensor structure of a high dimensional feature space, more efficiently improves the performance of machine learning algorithms. One encounters the \emph{curse of dimensionality}, and working with vectorized data fails to preserve the data structure. To mitigate the nonlinear relationship of tensor data more economically, we propose the \emph{Tensor Train Multi-way Multi-level Kernel (TT-MMK)}. This technique combines kernel filtering of the initial input data (\emph{Kernelized Tensor Train (KTT)}), stable reparametrization of the KTT in the Canonical Polyadic (CP) format, and the Dual Structure-preserving Support Vector Machine (\emph{SVM}) Kernel for revealing nonlinear relationships. We demonstrate numerically that the TT-MMK method is more reliable computationally, is less sensitive to tuning parameters, and gives higher prediction accuracy in the SVM classification compared to similar tensorised SVM methods.