Physics-Informed DeepONets for drift-diffusion on metric graphs: simulation and parameter identification

We develop a novel physics informed deep learning approach for solving nonlinear drift-diffusion equations on metric graphs. These models represent an important model class with a large number of applications in areas ranging from transport in biological cells to the motion of human crowds. While traditional numerical schemes require a large amount of tailoring, especially in the case of model design or parameter identification problems, physics informed deep operator networks (DeepONet) have emerged as a versatile tool for the solution of partial differential equations with the particular advantage that they easily incorporate parameter identification questions. We here present an approach where we first learn three DeepONet models for representative inflow, inner and outflow edges, resp., and then subsequently couple these models for the solution of the drift-diffusion metric graph problem by relying on an edge-based domain decomposition approach. We illustrate that our framework is applicable for the accurate evaluation of graph-coupled physics models and is well suited for solving optimization or inverse problems on these coupled networks.

Low-rank computation of the posterior mean in Multi-Output Gaussian Processes

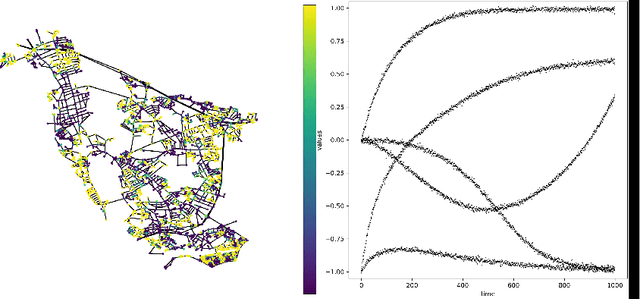
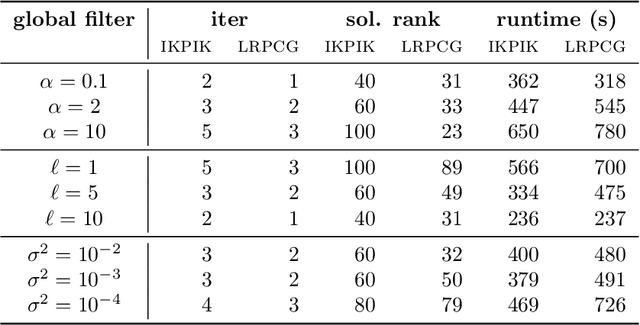
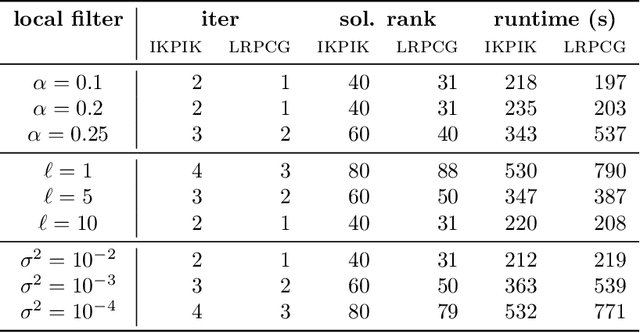
Gaussian processes (GP) are a versatile tool in machine learning and computational science. We here consider the case of multi-output Gaussian processes (MOGP) and present low-rank approaches for efficiently computing the posterior mean of a MOGP. Starting from low-rank spatio-temporal data we consider a structured covariance function, assuming separability across space and time. This separability, in turn, gives a decomposition of the covariance matrix into a Kronecker product of individual covariance matrices. Incorporating the typical noise term to the model then requires the solution of a large-scale Stein equation for computing the posterior mean. For this, we propose efficient low-rank methods based on a combination of a LRPCG method with the Sylvester equation solver KPIK adjusted for solving Stein equations. We test the developed method on real world street network graphs by using graph filters as covariance matrices. Moreover, we propose a degree-weighted average covariance matrix, which can be employed under specific assumptions to achieve more efficient convergence.

Preconditioned Additive Gaussian Processes with Fourier Acceleration

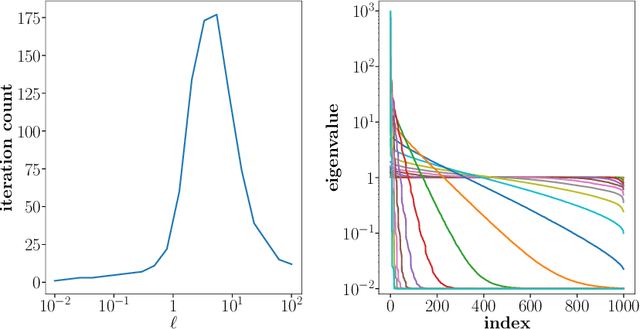
Gaussian processes (GPs) are crucial in machine learning for quantifying uncertainty in predictions. However, their associated covariance matrices, defined by kernel functions, are typically dense and large-scale, posing significant computational challenges. This paper introduces a matrix-free method that utilizes the Non-equispaced Fast Fourier Transform (NFFT) to achieve nearly linear complexity in the multiplication of kernel matrices and their derivatives with vectors for a predetermined accuracy level. To address high-dimensional problems, we propose an additive kernel approach. Each sub-kernel in this approach captures lower-order feature interactions, allowing for the efficient application of the NFFT method and potentially increasing accuracy across various real-world datasets. Additionally, we implement a preconditioning strategy that accelerates hyperparameter tuning, further improving the efficiency and effectiveness of GPs.

Fast Evaluation of Additive Kernels: Feature Arrangement, Fourier Methods, and Kernel Derivatives

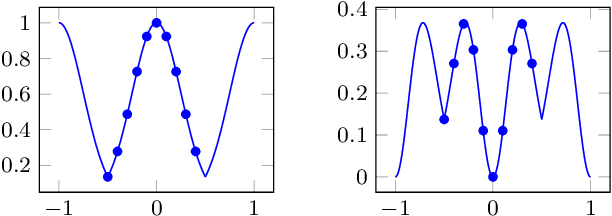
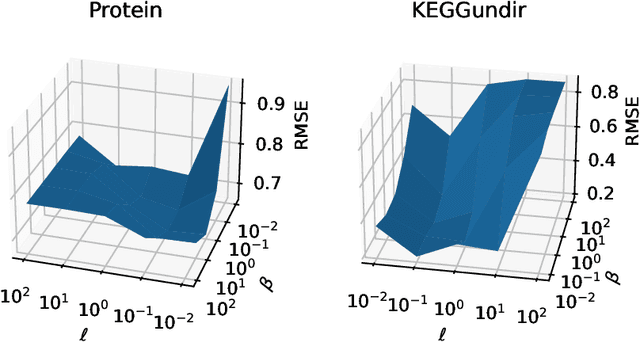
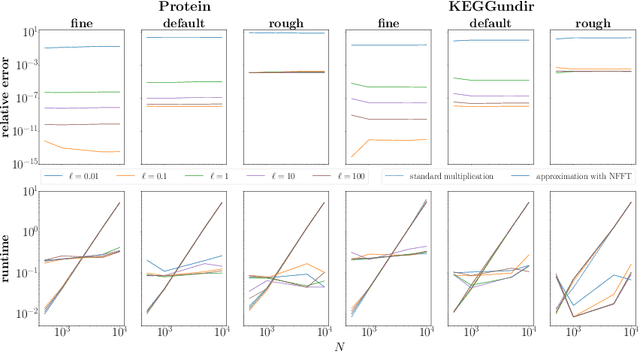
One of the main computational bottlenecks when working with kernel based learning is dealing with the large and typically dense kernel matrix. Techniques dealing with fast approximations of the matrix vector product for these kernel matrices typically deteriorate in their performance if the feature vectors reside in higher-dimensional feature spaces. We here present a technique based on the non-equispaced fast Fourier transform (NFFT) with rigorous error analysis. We show that this approach is also well suited to allow the approximation of the matrix that arises when the kernel is differentiated with respect to the kernel hyperparameters; a problem often found in the training phase of methods such as Gaussian processes. We also provide an error analysis for this case. We illustrate the performance of the additive kernel scheme with fast matrix vector products on a number of data sets. Our code is available at https://github.com/wagnertheresa/NFFTAddKer

Can Vehicle Motion Planning Generalize to Realistic Long-tail Scenarios?

Real-world autonomous driving systems must make safe decisions in the face of rare and diverse traffic scenarios. Current state-of-the-art planners are mostly evaluated on real-world datasets like nuScenes (open-loop) or nuPlan (closed-loop). In particular, nuPlan seems to be an expressive evaluation method since it is based on real-world data and closed-loop, yet it mostly covers basic driving scenarios. This makes it difficult to judge a planner's capabilities to generalize to rarely-seen situations. Therefore, we propose a novel closed-loop benchmark interPlan containing several edge cases and challenging driving scenarios. We assess existing state-of-the-art planners on our benchmark and show that neither rule-based nor learning-based planners can safely navigate the interPlan scenarios. A recently evolving direction is the usage of foundation models like large language models (LLM) to handle generalization. We evaluate an LLM-only planner and introduce a novel hybrid planner that combines an LLM-based behavior planner with a rule-based motion planner that achieves state-of-the-art performance on our benchmark.

A Preconditioned Interior Point Method for Support Vector Machines Using an ANOVA-Decomposition and NFFT-Based Matrix-Vector Products

In this paper we consider the numerical solution to the soft-margin support vector machine optimization problem. This problem is typically solved using the SMO algorithm, given the high computational complexity of traditional optimization algorithms when dealing with large-scale kernel matrices. In this work, we propose employing an NFFT-accelerated matrix-vector product using an ANOVA decomposition for the feature space that is used within an interior point method for the overall optimization problem. As this method requires the solution of a linear system of saddle point form we suggest a preconditioning approach that is based on low-rank approximations of the kernel matrix together with a Krylov subspace solver. We compare the accuracy of the ANOVA-based kernel with the default LIBSVM implementation. We investigate the performance of the different preconditioners as well as the accuracy of the ANOVA kernel on several large-scale datasets.

Rethinking Integration of Prediction and Planning in Deep Learning-Based Automated Driving Systems: A Review

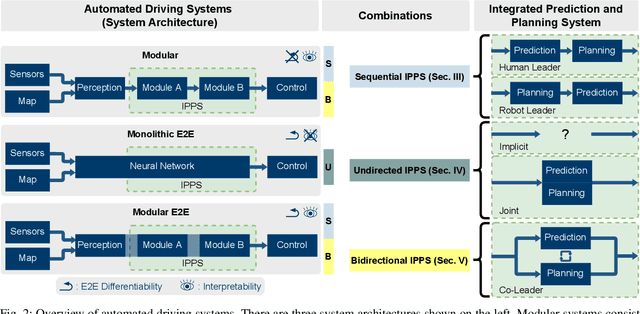
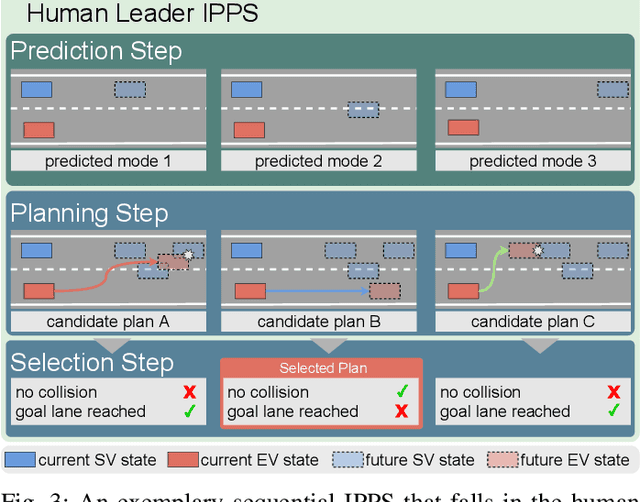
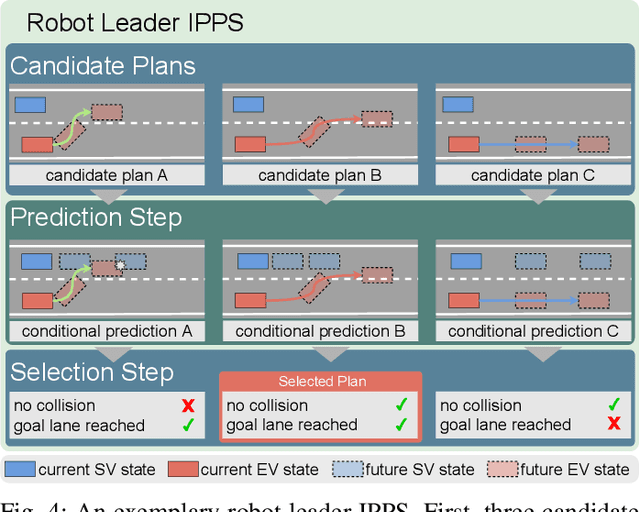
Automated driving has the potential to revolutionize personal, public, and freight mobility. Besides the enormous challenge of perception, i.e. accurately perceiving the environment using available sensor data, automated driving comprises planning a safe, comfortable, and efficient motion trajectory. To promote safety and progress, many works rely on modules that predict the future motion of surrounding traffic. Modular automated driving systems commonly handle prediction and planning as sequential separate tasks. While this accounts for the influence of surrounding traffic on the ego-vehicle, it fails to anticipate the reactions of traffic participants to the ego-vehicle's behavior. Recent works suggest that integrating prediction and planning in an interdependent joint step is necessary to achieve safe, efficient, and comfortable driving. While various models implement such integrated systems, a comprehensive overview and theoretical understanding of different principles are lacking. We systematically review state-of-the-art deep learning-based prediction, planning, and integrated prediction and planning models. Different facets of the integration ranging from model architecture and model design to behavioral aspects are considered and related to each other. Moreover, we discuss the implications, strengths, and limitations of different integration methods. By pointing out research gaps, describing relevant future challenges, and highlighting trends in the research field, we identify promising directions for future research.

Stay on Track: A Frenet Wrapper to Overcome Off-road Trajectories in Vehicle Motion Prediction

Predicting the future motion of observed vehicles is a crucial enabler for safe autonomous driving. The field of motion prediction has seen large progress recently with State-of-the-Art (SotA) models achieving impressive results on large-scale public benchmarks. However, recent work revealed that learning-based methods are prone to predict off-road trajectories in challenging scenarios. These can be created by perturbing existing scenarios with additional turns in front of the target vehicle while the motion history is left unchanged. We argue that this indicates that SotA models do not consider the map information sufficiently and demonstrate how this can be solved, by representing model inputs and outputs in a Frenet frame defined by lane centreline sequences. To this end, we present a general wrapper that leverages a Frenet representation of the scene and that can be applied to SotA models without changing their architecture. We demonstrate the effectiveness of this approach in a comprehensive benchmark using two SotA motion prediction models. Our experiments show that this reduces the off-road rate on challenging scenarios by more than 90\%, without sacrificing average performance.

Scaling Planning for Automated Driving using Simplistic Synthetic Data

We challenge the perceived consensus that the application of deep learning to solve the automated driving planning task requires a huge amount of real-world data or a realistic simulator. Using a roundabout scenario, we show that this requirement can be relaxed in favour of targeted, simplistic simulated data. A benefit is that such data can be easily generated for critical scenarios that are typically underrepresented in realistic datasets. By applying vanilla behavioural cloning almost exclusively to lightweight simulated data, we achieve reliable and comfortable real-world driving. Our key insight lies in an incremental development approach that includes regular in-vehicle testing to identify sim-to-real gaps, targeted data augmentation, and training scenario variations. In addition to the methodology, we offer practical guidelines for deploying such a policy within a real-world vehicle, along with insights of the resulting qualitative driving behaviour. This approach serves as a blueprint for many automated driving use cases, providing valuable insights for future research and helping develop efficient and effective solutions.

A weighted subspace exponential kernel for support tensor machines

High-dimensional data in the form of tensors are challenging for kernel classification methods. To both reduce the computational complexity and extract informative features, kernels based on low-rank tensor decompositions have been proposed. However, what decisive features of the tensors are exploited by these kernels is often unclear. In this paper we propose a novel kernel that is based on the Tucker decomposition. For this kernel the Tucker factors are computed based on re-weighting of the Tucker matrices with tuneable powers of singular values from the HOSVD decomposition. This provides a mechanism to balance the contribution of the Tucker core and factors of the data. We benchmark support tensor machines with this new kernel on several datasets. First we generate synthetic data where two classes differ in either Tucker factors or core, and compare our novel and previously existing kernels. We show robustness of the new kernel with respect to both classification scenarios. We further test the new method on real-world datasets. The proposed kernel has demonstrated a higher test accuracy than the state-of-the-art tensor train multi-way multi-level kernel, and a significantly lower computational time.