Fast Evaluation of Additive Kernels: Feature Arrangement, Fourier Methods, and Kernel Derivatives

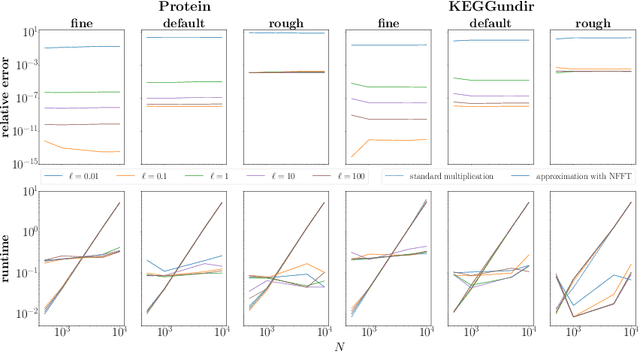
One of the main computational bottlenecks when working with kernel based learning is dealing with the large and typically dense kernel matrix. Techniques dealing with fast approximations of the matrix vector product for these kernel matrices typically deteriorate in their performance if the feature vectors reside in higher-dimensional feature spaces. We here present a technique based on the non-equispaced fast Fourier transform (NFFT) with rigorous error analysis. We show that this approach is also well suited to allow the approximation of the matrix that arises when the kernel is differentiated with respect to the kernel hyperparameters; a problem often found in the training phase of methods such as Gaussian processes. We also provide an error analysis for this case. We illustrate the performance of the additive kernel scheme with fast matrix vector products on a number of data sets. Our code is available at https://github.com/wagnertheresa/NFFTAddKer

Fast and interpretable Support Vector Classification based on the truncated ANOVA decomposition

Support Vector Machines (SVMs) are an important tool for performing classification on scattered data, where one usually has to deal with many data points in high-dimensional spaces. We propose solving SVMs in primal form using feature maps based on trigonometric functions or wavelets. In small dimensional settings the Fast Fourier Transform (FFT) and related methods are a powerful tool in order to deal with the considered basis functions. For growing dimensions the classical FFT-based methods become inefficient due to the curse of dimensionality. Therefore, we restrict ourselves to multivariate basis functions, each one of them depends only on a small number of dimensions. This is motivated by the well-known sparsity of effects and recent results regarding the reconstruction of functions from scattered data in terms of truncated analysis of variance (ANOVA) decomposition, which makes the resulting model even interpretable in terms of importance of the features as well as their couplings. The usage of small superposition dimensions has the consequence that the computational effort no longer grows exponentially but only polynomially with respect to the dimension. In order to enforce sparsity regarding the basis coefficients, we use the frequently applied $\ell_2$-norm and, in addition, $\ell_1$-norm regularization. The found classifying function, which is the linear combination of basis functions, and its variance can then be analyzed in terms of the classical ANOVA decomposition of functions. Based on numerical examples we show that we are able to recover the signum of a function that perfectly fits our model assumptions. We obtain better results with $\ell_1$-norm regularization, both in terms of accuracy and clarity of interpretability.

Learning in High-Dimensional Feature Spaces Using ANOVA-Based Fast Matrix-Vector Multiplication

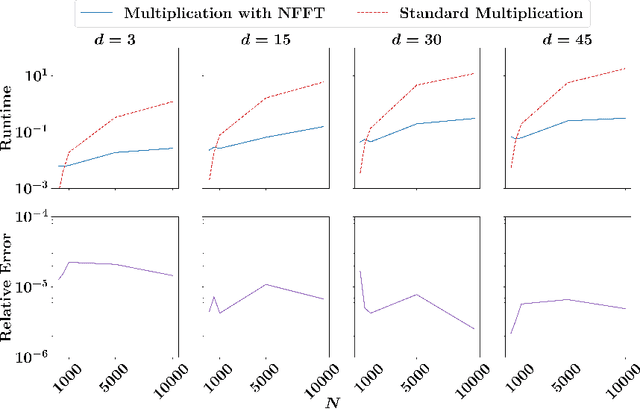
Kernel matrices are crucial in many learning tasks such as support vector machines or kernel ridge regression. The kernel matrix is typically dense and large-scale. Depending on the dimension of the feature space even the computation of all of its entries in reasonable time becomes a challenging task. For such dense matrices the cost of a matrix-vector product scales quadratically in the number of entries, if no customized methods are applied. We propose the use of an ANOVA kernel, where we construct several kernels based on lower-dimensional feature spaces for which we provide fast algorithms realizing the matrix-vector products. We employ the non-equispaced fast Fourier transform (NFFT), which is of linear complexity for fixed accuracy. Based on a feature grouping approach, we then show how the fast matrix-vector products can be embedded into a learning method choosing kernel ridge regression and the preconditioned conjugate gradient solver. We illustrate the performance of our approach on several data sets.