ANOVA-boosting for Random Fourier Features

We propose two algorithms for boosting random Fourier feature models for approximating high-dimensional functions. These methods utilize the classical and generalized analysis of variance (ANOVA) decomposition to learn low-order functions, where there are few interactions between the variables. Our algorithms are able to find an index set of important input variables and variable interactions reliably. Furthermore, we generalize already existing random Fourier feature models to an ANOVA setting, where terms of different order can be used. Our algorithms have the advantage of interpretability, meaning that the influence of every input variable is known in the learned model, even for dependent input variables. We give theoretical as well as numerical results that our algorithms perform well for sensitivity analysis. The ANOVA-boosting step reduces the approximation error of existing methods significantly.

Fast and interpretable Support Vector Classification based on the truncated ANOVA decomposition

Support Vector Machines (SVMs) are an important tool for performing classification on scattered data, where one usually has to deal with many data points in high-dimensional spaces. We propose solving SVMs in primal form using feature maps based on trigonometric functions or wavelets. In small dimensional settings the Fast Fourier Transform (FFT) and related methods are a powerful tool in order to deal with the considered basis functions. For growing dimensions the classical FFT-based methods become inefficient due to the curse of dimensionality. Therefore, we restrict ourselves to multivariate basis functions, each one of them depends only on a small number of dimensions. This is motivated by the well-known sparsity of effects and recent results regarding the reconstruction of functions from scattered data in terms of truncated analysis of variance (ANOVA) decomposition, which makes the resulting model even interpretable in terms of importance of the features as well as their couplings. The usage of small superposition dimensions has the consequence that the computational effort no longer grows exponentially but only polynomially with respect to the dimension. In order to enforce sparsity regarding the basis coefficients, we use the frequently applied $\ell_2$-norm and, in addition, $\ell_1$-norm regularization. The found classifying function, which is the linear combination of basis functions, and its variance can then be analyzed in terms of the classical ANOVA decomposition of functions. Based on numerical examples we show that we are able to recover the signum of a function that perfectly fits our model assumptions. We obtain better results with $\ell_1$-norm regularization, both in terms of accuracy and clarity of interpretability.

Interpretable transformed ANOVA approximation on the example of the prevention of forest fires

The distribution of data points is a key component in machine learning. In most cases, one uses min-max normalization to obtain nodes in $[0,1]$ or Z-score normalization for standard normal distributed data. In this paper, we apply transformation ideas in order to design a complete orthonormal system in the $\mathrm{L}_2$ space of functions with the standard normal distribution as integration weight. Subsequently, we are able to apply the explainable ANOVA approximation for this basis and use Z-score transformed data in the method. We demonstrate the applicability of this procedure on the well-known forest fires data set from the UCI machine learning repository. The attribute ranking obtained from the ANOVA approximation provides us with crucial information about which variables in the data set are the most important for the detection of fires.

Interpretable Approximation of High-Dimensional Data

In this paper we apply the previously introduced approximation method based on the ANOVA (analysis of variance) decomposition and Grouped Transformations to synthetic and real data. The advantage of this method is the interpretability of the approximation, i.e., the ability to rank the importance of the attribute interactions or the variable couplings. Moreover, we are able to generate an attribute ranking to identify unimportant variables and reduce the dimensionality of the problem. We compare the method to other approaches on publicly available benchmark datasets.

NFFT meets Krylov methods: Fast matrix-vector products for the graph Laplacian of fully connected networks

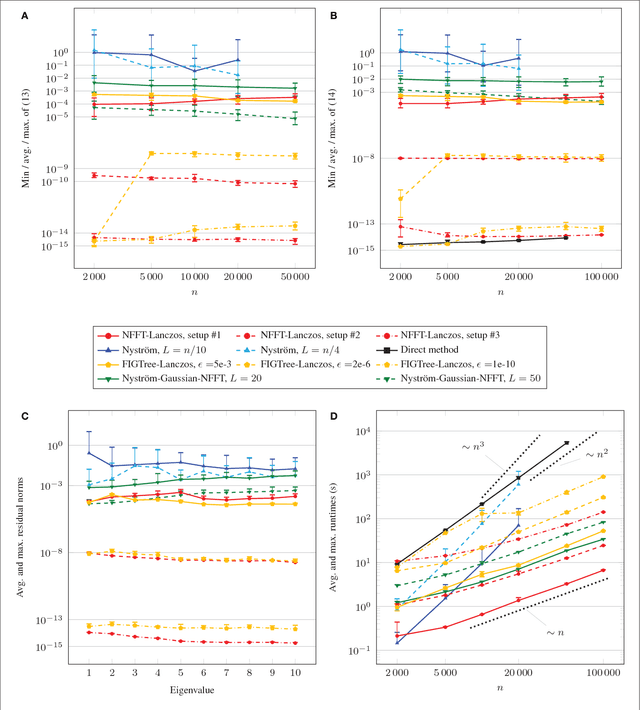
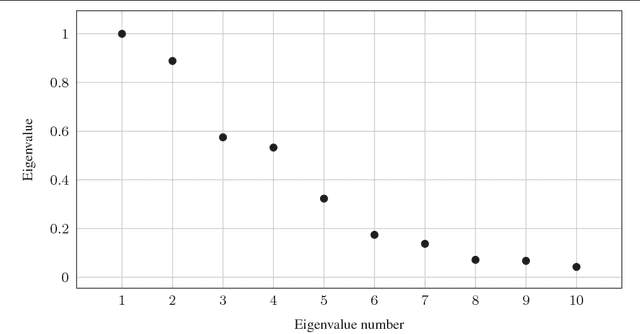
The graph Laplacian is a standard tool in data science, machine learning, and image processing. The corresponding matrix inherits the complex structure of the underlying network and is in certain applications densely populated. This makes computations, in particular matrix-vector products, with the graph Laplacian a hard task. A typical application is the computation of a number of its eigenvalues and eigenvectors. Standard methods become infeasible as the number of nodes in the graph is too large. We propose the use of the fast summation based on the nonequispaced fast Fourier transform (NFFT) to perform the dense matrix-vector product with the graph Laplacian fast without ever forming the whole matrix. The enormous flexibility of the NFFT algorithm allows us to embed the accelerated multiplication into Lanczos-based eigenvalues routines or iterative linear system solvers. We illustrate the feasibility of our approach on a number of test problems from image segmentation to semi-supervised learning based on graph-based PDEs. In particular, we compare our approach with the Nystr\"om method. Moreover, we present and test an enhanced, hybrid version of the Nystr\"om method, which internally uses the NFFT.