Semi-supervised Learning for Multilayer Graphs Using Diffuse Interface Methods and Fast Matrix Vector Products

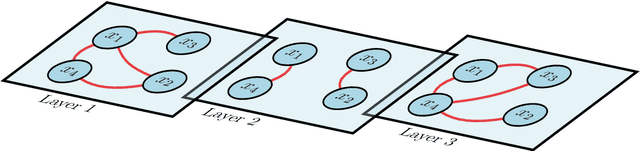
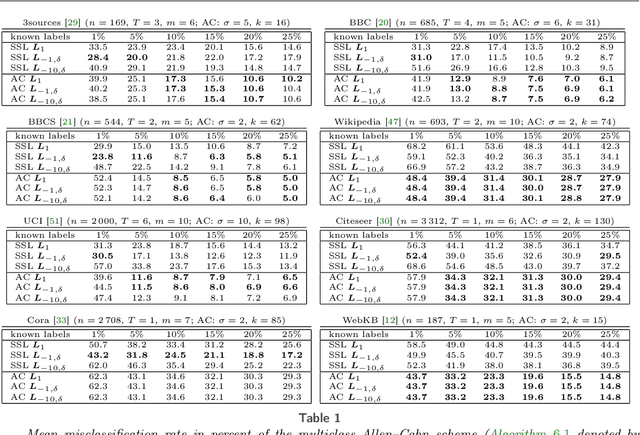
We generalize a graph-based multiclass semi-supervised classification technique based on diffuse interface methods to multilayer graphs allowing for a very high number of layers. Besides the treatment of various applications with an inherent multilayer structure, we present a very flexible approach that interprets high-dimensional data in a low-dimensional multilayer graph representation. Highly efficient numerical methods involving the spectral decomposition of the corresponding differential graph operators as well as fast matrix-vector products based on the nonequispaced fast Fourier transform (NFFT) enable the rapid treatment of very large data sets and make the algorithm independent of specialized hardware as well as scalable to even larger problems. We test the performance of our method on a variety of large and high-dimensional data sets.

NFFT meets Krylov methods: Fast matrix-vector products for the graph Laplacian of fully connected networks

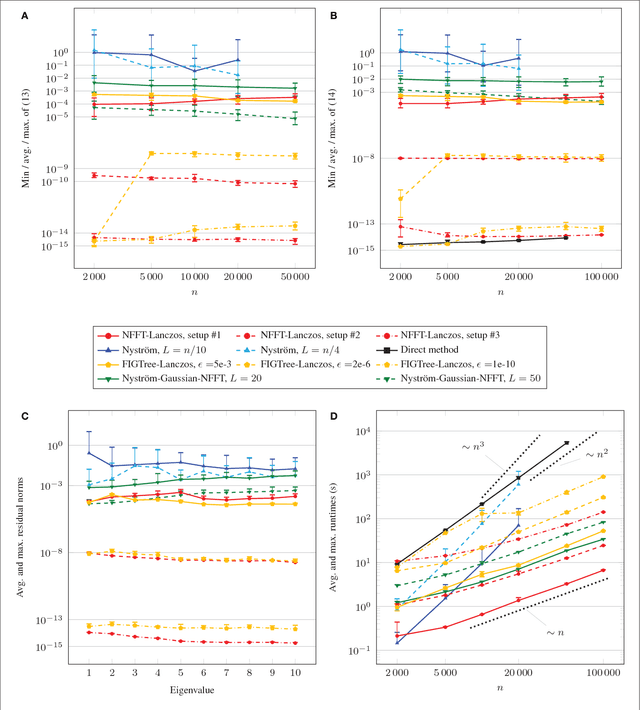
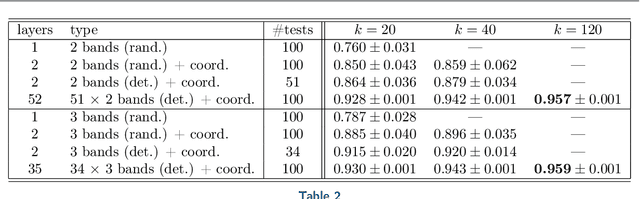
The graph Laplacian is a standard tool in data science, machine learning, and image processing. The corresponding matrix inherits the complex structure of the underlying network and is in certain applications densely populated. This makes computations, in particular matrix-vector products, with the graph Laplacian a hard task. A typical application is the computation of a number of its eigenvalues and eigenvectors. Standard methods become infeasible as the number of nodes in the graph is too large. We propose the use of the fast summation based on the nonequispaced fast Fourier transform (NFFT) to perform the dense matrix-vector product with the graph Laplacian fast without ever forming the whole matrix. The enormous flexibility of the NFFT algorithm allows us to embed the accelerated multiplication into Lanczos-based eigenvalues routines or iterative linear system solvers. We illustrate the feasibility of our approach on a number of test problems from image segmentation to semi-supervised learning based on graph-based PDEs. In particular, we compare our approach with the Nystr\"om method. Moreover, we present and test an enhanced, hybrid version of the Nystr\"om method, which internally uses the NFFT.