Dominik Alfke
A Study of Graph-Based Approaches for Semi-Supervised Time Series Classification
Apr 16, 2021
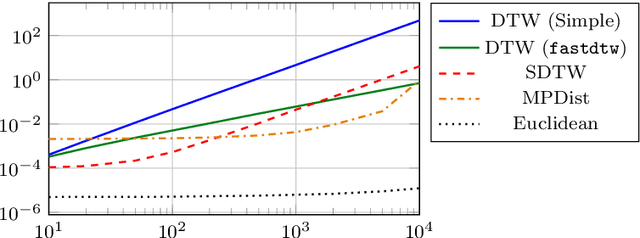

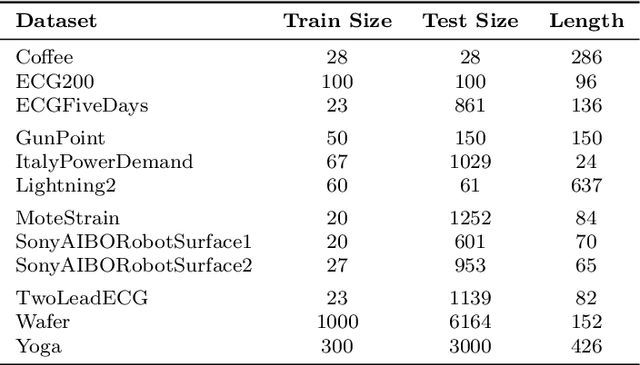
Abstract:Time series data play an important role in many applications and their analysis reveals crucial information for understanding the underlying processes. Among the many time series learning tasks of great importance, we here focus on semi-supervised learning which benefits of a graph representation of the data. Two main aspects are involved in this task: A suitable distance measure to evaluate the similarities between time series, and a learning method to make predictions based on these distances. However, the relationship between the two aspects has never been studied systematically. We describe four different distance measures, including (Soft) DTW and Matrix Profile, as well as four successful semi-supervised learning methods, including the graph Allen- Cahn method and a Graph Convolutional Neural Network. We then compare the performance of the algorithms on standard data sets. Our findings show that all measures and methods vary strongly in accuracy between data sets and that there is no clear best combination to employ in all cases.
Pseudoinverse Graph Convolutional Networks: Fast Filters Tailored for Large Eigengaps of Dense Graphs and Hypergraphs
Aug 03, 2020


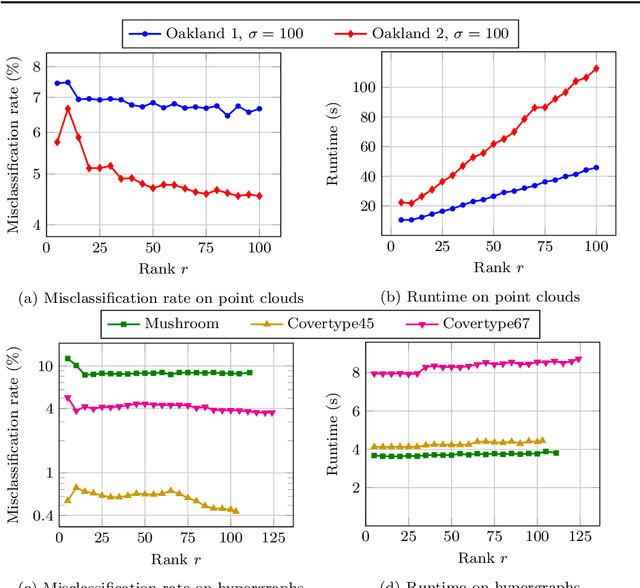
Abstract:Graph Convolutional Networks (GCNs) have proven to be successful tools for semi-supervised classification on graph-based datasets. We propose a new GCN variant whose three-part filter space is targeted at dense graphs. Examples include Gaussian graphs for 3D point clouds with an increased focus on non-local information, as well as hypergraphs based on categorical data. These graphs differ from the common sparse benchmark graphs in terms of the spectral properties of their graph Laplacian. Most notably we observe large eigengaps, which are unfavorable for popular existing GCN architectures. Our method overcomes these issues by utilizing the pseudoinverse of the Laplacian. Another key ingredient is a low-rank approximation of the convolutional matrix, ensuring computational efficiency and increasing accuracy at the same time. We outline how the necessary eigeninformation can be computed efficiently in each applications and discuss the appropriate choice of the only metaparameter, the approximation rank. We finally showcase our method's performance regarding runtime and accuracy in various experiments with real-world datasets.
Semi-Supervised Classification on Non-Sparse Graphs Using Low-Rank Graph Convolutional Networks
May 24, 2019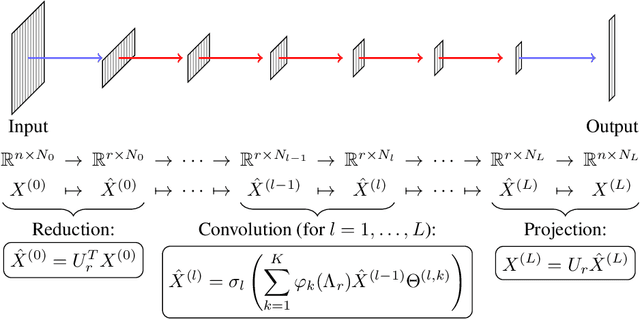
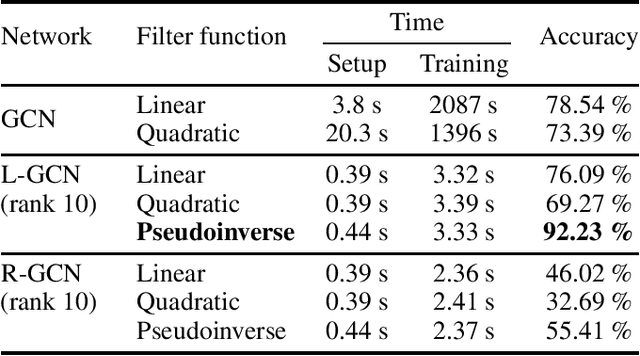
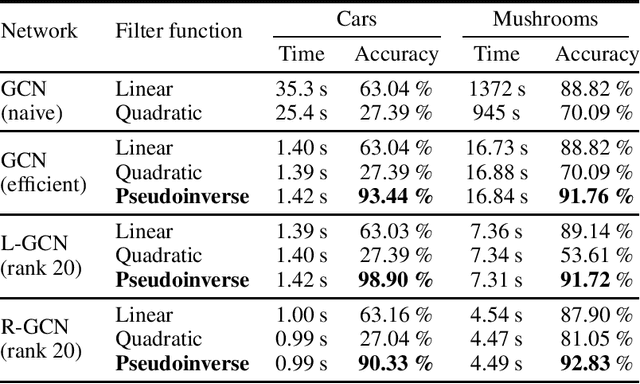

Abstract:Graph Convolutional Networks (GCNs) have proven to be successful tools for semi-supervised learning on graph-based datasets. For sparse graphs, linear and polynomial filter functions have yielded impressive results. For large non-sparse graphs, however, network training and evaluation becomes prohibitively expensive. By introducing low-rank filters, we gain significant runtime acceleration and simultaneously improved accuracy. We further propose an architecture change mimicking techniques from Model Order Reduction in what we call a reduced-order GCN. Moreover, we present how our method can also be applied to hypergraph datasets and how hypergraph convolution can be implemented efficiently.
The Oracle of DLphi
Jan 27, 2019Abstract:We present a novel technique based on deep learning and set theory which yields exceptional classification and prediction results. Having access to a sufficiently large amount of labelled training data, our methodology is capable of predicting the labels of the test data almost always even if the training data is entirely unrelated to the test data. In other words, we prove in a specific setting that as long as one has access to enough data points, the quality of the data is irrelevant.
NFFT meets Krylov methods: Fast matrix-vector products for the graph Laplacian of fully connected networks
Aug 14, 2018

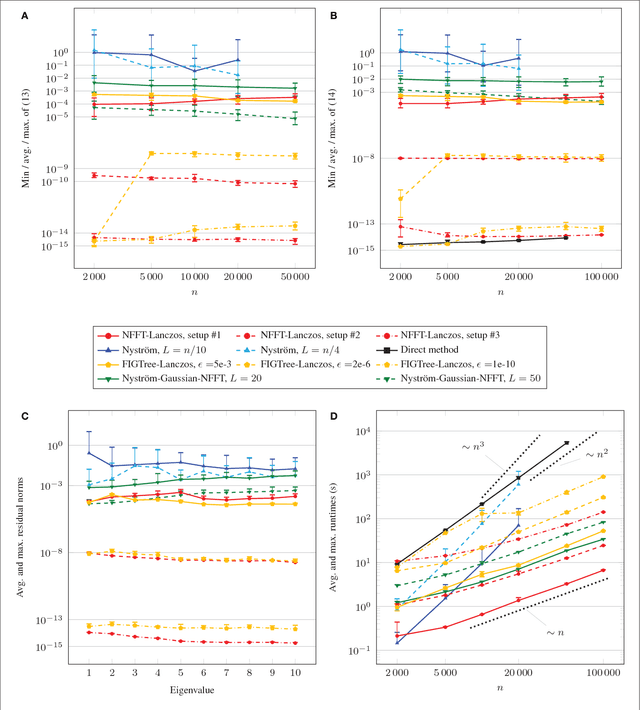
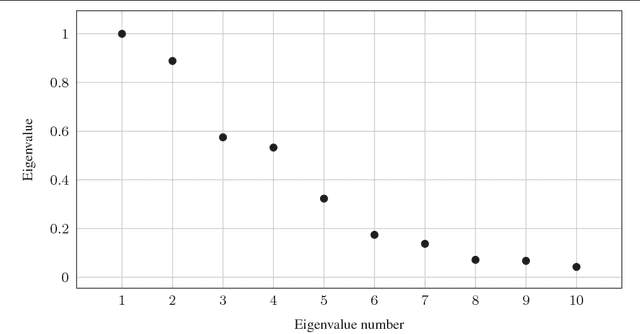
Abstract:The graph Laplacian is a standard tool in data science, machine learning, and image processing. The corresponding matrix inherits the complex structure of the underlying network and is in certain applications densely populated. This makes computations, in particular matrix-vector products, with the graph Laplacian a hard task. A typical application is the computation of a number of its eigenvalues and eigenvectors. Standard methods become infeasible as the number of nodes in the graph is too large. We propose the use of the fast summation based on the nonequispaced fast Fourier transform (NFFT) to perform the dense matrix-vector product with the graph Laplacian fast without ever forming the whole matrix. The enormous flexibility of the NFFT algorithm allows us to embed the accelerated multiplication into Lanczos-based eigenvalues routines or iterative linear system solvers. We illustrate the feasibility of our approach on a number of test problems from image segmentation to semi-supervised learning based on graph-based PDEs. In particular, we compare our approach with the Nystr\"om method. Moreover, we present and test an enhanced, hybrid version of the Nystr\"om method, which internally uses the NFFT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge