Fast Evaluation of Additive Kernels: Feature Arrangement, Fourier Methods, and Kernel Derivatives

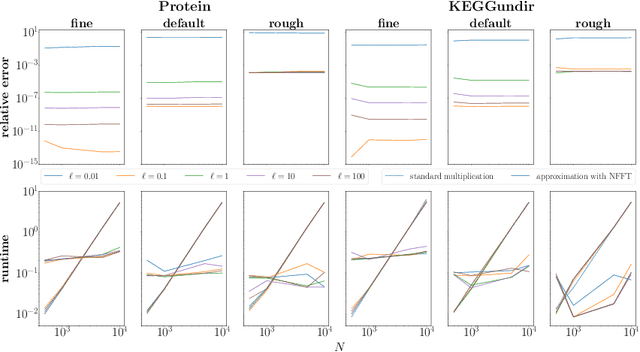
One of the main computational bottlenecks when working with kernel based learning is dealing with the large and typically dense kernel matrix. Techniques dealing with fast approximations of the matrix vector product for these kernel matrices typically deteriorate in their performance if the feature vectors reside in higher-dimensional feature spaces. We here present a technique based on the non-equispaced fast Fourier transform (NFFT) with rigorous error analysis. We show that this approach is also well suited to allow the approximation of the matrix that arises when the kernel is differentiated with respect to the kernel hyperparameters; a problem often found in the training phase of methods such as Gaussian processes. We also provide an error analysis for this case. We illustrate the performance of the additive kernel scheme with fast matrix vector products on a number of data sets. Our code is available at https://github.com/wagnertheresa/NFFTAddKer

A Preconditioned Interior Point Method for Support Vector Machines Using an ANOVA-Decomposition and NFFT-Based Matrix-Vector Products

In this paper we consider the numerical solution to the soft-margin support vector machine optimization problem. This problem is typically solved using the SMO algorithm, given the high computational complexity of traditional optimization algorithms when dealing with large-scale kernel matrices. In this work, we propose employing an NFFT-accelerated matrix-vector product using an ANOVA decomposition for the feature space that is used within an interior point method for the overall optimization problem. As this method requires the solution of a linear system of saddle point form we suggest a preconditioning approach that is based on low-rank approximations of the kernel matrix together with a Krylov subspace solver. We compare the accuracy of the ANOVA-based kernel with the default LIBSVM implementation. We investigate the performance of the different preconditioners as well as the accuracy of the ANOVA kernel on several large-scale datasets.

Learning in High-Dimensional Feature Spaces Using ANOVA-Based Fast Matrix-Vector Multiplication

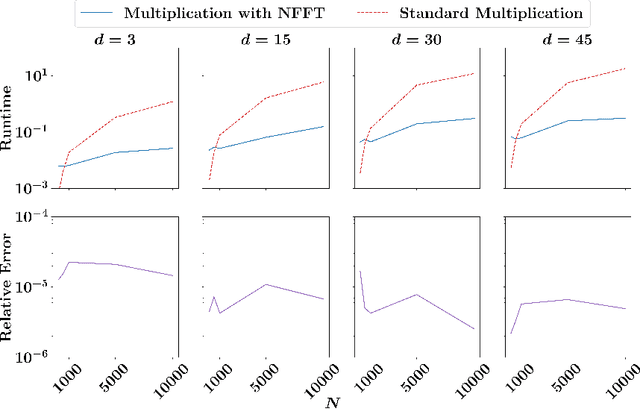
Kernel matrices are crucial in many learning tasks such as support vector machines or kernel ridge regression. The kernel matrix is typically dense and large-scale. Depending on the dimension of the feature space even the computation of all of its entries in reasonable time becomes a challenging task. For such dense matrices the cost of a matrix-vector product scales quadratically in the number of entries, if no customized methods are applied. We propose the use of an ANOVA kernel, where we construct several kernels based on lower-dimensional feature spaces for which we provide fast algorithms realizing the matrix-vector products. We employ the non-equispaced fast Fourier transform (NFFT), which is of linear complexity for fixed accuracy. Based on a feature grouping approach, we then show how the fast matrix-vector products can be embedded into a learning method choosing kernel ridge regression and the preconditioned conjugate gradient solver. We illustrate the performance of our approach on several data sets.