Fast Evaluation of Additive Kernels: Feature Arrangement, Fourier Methods, and Kernel Derivatives

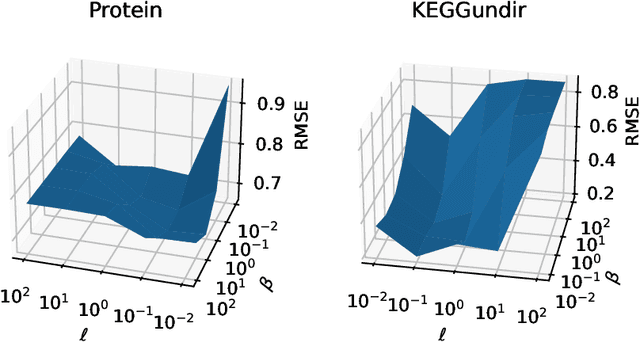
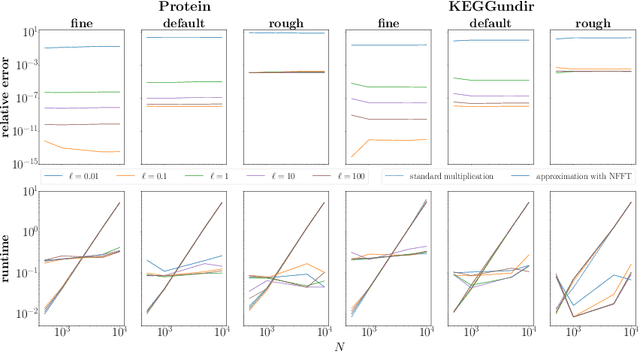
One of the main computational bottlenecks when working with kernel based learning is dealing with the large and typically dense kernel matrix. Techniques dealing with fast approximations of the matrix vector product for these kernel matrices typically deteriorate in their performance if the feature vectors reside in higher-dimensional feature spaces. We here present a technique based on the non-equispaced fast Fourier transform (NFFT) with rigorous error analysis. We show that this approach is also well suited to allow the approximation of the matrix that arises when the kernel is differentiated with respect to the kernel hyperparameters; a problem often found in the training phase of methods such as Gaussian processes. We also provide an error analysis for this case. We illustrate the performance of the additive kernel scheme with fast matrix vector products on a number of data sets. Our code is available at https://github.com/wagnertheresa/NFFTAddKer