Learning in High-Dimensional Feature Spaces Using ANOVA-Based Fast Matrix-Vector Multiplication
Paper and Code
Nov 19, 2021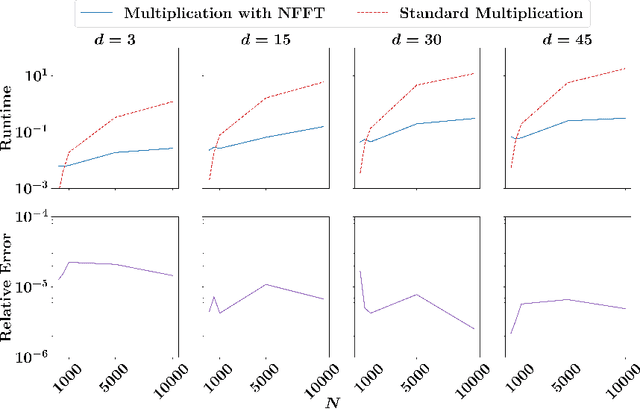


Kernel matrices are crucial in many learning tasks such as support vector machines or kernel ridge regression. The kernel matrix is typically dense and large-scale. Depending on the dimension of the feature space even the computation of all of its entries in reasonable time becomes a challenging task. For such dense matrices the cost of a matrix-vector product scales quadratically in the number of entries, if no customized methods are applied. We propose the use of an ANOVA kernel, where we construct several kernels based on lower-dimensional feature spaces for which we provide fast algorithms realizing the matrix-vector products. We employ the non-equispaced fast Fourier transform (NFFT), which is of linear complexity for fixed accuracy. Based on a feature grouping approach, we then show how the fast matrix-vector products can be embedded into a learning method choosing kernel ridge regression and the preconditioned conjugate gradient solver. We illustrate the performance of our approach on several data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge