Greedy inference with layers of lazy maps

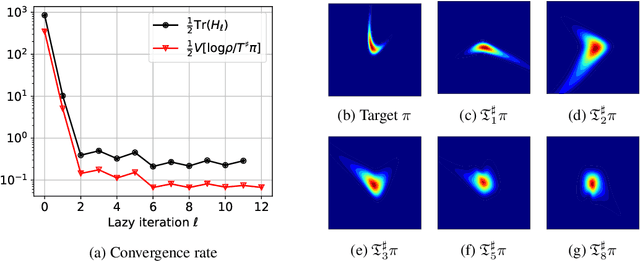
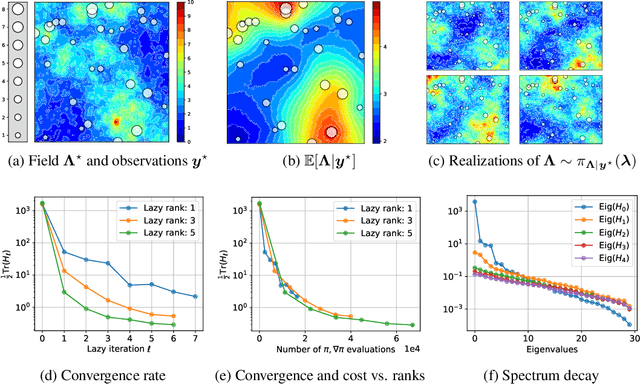
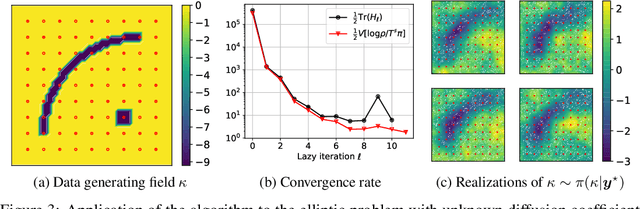
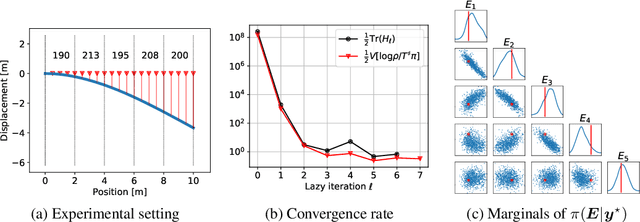
We propose a framework for the greedy approximation of high-dimensional Bayesian inference problems, through the composition of multiple \emph{low-dimensional} transport maps or flows. Our framework operates recursively on a sequence of ``residual'' distributions, given by pulling back the posterior through the previously computed transport maps. The action of each map is confined to a low-dimensional subspace that we identify by minimizing an error bound. At each step, our approach thus identifies (i) a relevant subspace of the residual distribution, and (ii) a low-dimensional transformation between a restriction of the residual onto this subspace and a standard Gaussian. We prove weak convergence of the approach to the posterior distribution, and we demonstrate the algorithm on a range of challenging inference problems in differential equations and spatial statistics.