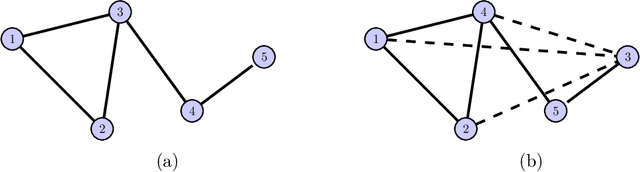
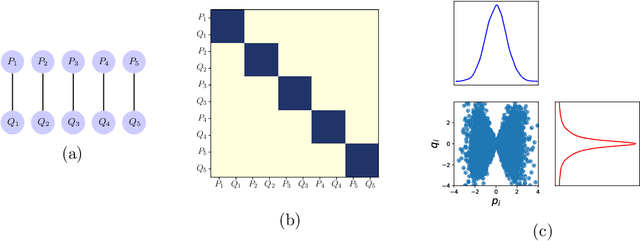
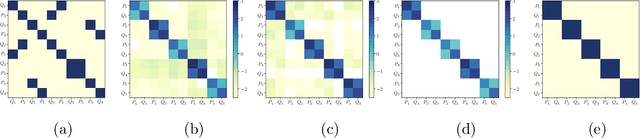
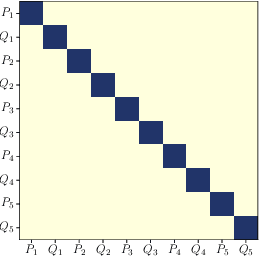
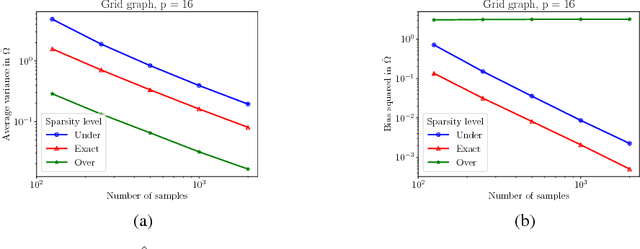
Learning non-Gaussian graphical models via Hessian scores and triangular transport

Undirected probabilistic graphical models represent the conditional dependencies, or Markov properties, of a collection of random variables. Knowing the sparsity of such a graphical model is valuable for modeling multivariate distributions and for efficiently performing inference. While the problem of learning graph structure from data has been studied extensively for certain parametric families of distributions, most existing methods fail to consistently recover the graph structure for non-Gaussian data. Here we propose an algorithm for learning the Markov structure of continuous and non-Gaussian distributions. To characterize conditional independence, we introduce a score based on integrated Hessian information from the joint log-density, and we prove that this score upper bounds the conditional mutual information for a general class of distributions. To compute the score, our algorithm SING estimates the density using a deterministic coupling, induced by a triangular transport map, and iteratively exploits sparse structure in the map to reveal sparsity in the graph. For certain non-Gaussian datasets, we show that our algorithm recovers the graph structure even with a biased approximation to the density. Among other examples, we apply sing to learn the dependencies between the states of a chaotic dynamical system with local interactions.

Beyond normality: Learning sparse probabilistic graphical models in the non-Gaussian setting

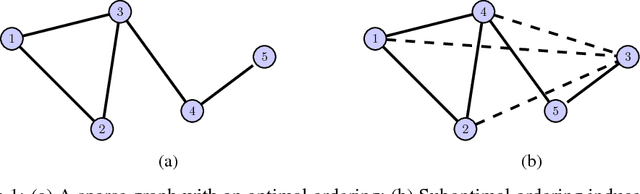
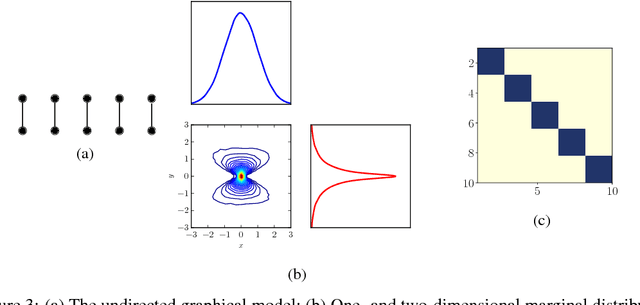
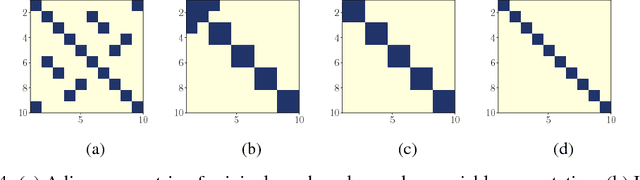
We present an algorithm to identify sparse dependence structure in continuous and non-Gaussian probability distributions, given a corresponding set of data. The conditional independence structure of an arbitrary distribution can be represented as an undirected graph (or Markov random field), but most algorithms for learning this structure are restricted to the discrete or Gaussian cases. Our new approach allows for more realistic and accurate descriptions of the distribution in question, and in turn better estimates of its sparse Markov structure. Sparsity in the graph is of interest as it can accelerate inference, improve sampling methods, and reveal important dependencies between variables. The algorithm relies on exploiting the connection between the sparsity of the graph and the sparsity of transport maps, which deterministically couple one probability measure to another.