BP-Seg: A graphical model approach to unsupervised and non-contiguous text segmentation using belief propagation

Text segmentation based on the semantic meaning of sentences is a fundamental task with broad utility in many downstream applications. In this paper, we propose a graphical model-based unsupervised learning approach, named BP-Seg for efficient text segmentation. Our method not only considers local coherence, capturing the intuition that adjacent sentences are often more related, but also effectively groups sentences that are distant in the text yet semantically similar. This is achieved through belief propagation on the carefully constructed graphical models. Experimental results on both an illustrative example and a dataset with long-form documents demonstrate that our method performs favorably compared to competing approaches.

Efficient AI in Practice: Training and Deployment of Efficient LLMs for Industry Applications

Large language models (LLMs) have demonstrated remarkable performance across a wide range of industrial applications, from search and recommendations to generative tasks. Although scaling laws indicate that larger models generally yield better generalization and performance, their substantial computational requirements often render them impractical for many real-world scenarios at scale. In this paper, we present methods and insights for training small language models (SLMs) that deliver high performance and efficiency in deployment. We focus on two key techniques: (1) knowledge distillation and (2) model compression via quantization and pruning. These approaches enable SLMs to retain much of the quality of their larger counterparts while significantly reducing training, serving costs, and latency. We detail the impact of these techniques on a variety of use cases at a large professional social network platform and share deployment lessons - including hardware optimization strategies that enhance speed and throughput for both predictive and reasoning-based applications.

AlphaPO -- Reward shape matters for LLM alignment

Reinforcement Learning with Human Feedback (RLHF) and its variants have made huge strides toward the effective alignment of large language models (LLMs) to follow instructions and reflect human values. More recently, Direct Alignment Algorithms (DAAs) have emerged in which the reward modeling stage of RLHF is skipped by characterizing the reward directly as a function of the policy being learned. Examples include Direct Preference Optimization (DPO) and Simple Preference Optimization (SimPO). These methods often suffer from likelihood displacement, a phenomenon by which the probabilities of preferred responses are often reduced undesirably. In this paper, we argue that, for DAAs the reward (function) shape matters. We introduce AlphaPO, a new DAA method that leverages an $\alpha$-parameter to help change the shape of the reward function beyond the standard log reward. AlphaPO helps maintain fine-grained control over likelihood displacement and over-optimization. Compared to SimPO, one of the best performing DAAs, AlphaPO leads to about 7\% to 10\% relative improvement in alignment performance for the instruct versions of Mistral-7B and Llama3-8B. The analysis and results presented highlight the importance of the reward shape, and how one can systematically change it to affect training dynamics, as well as improve alignment performance.

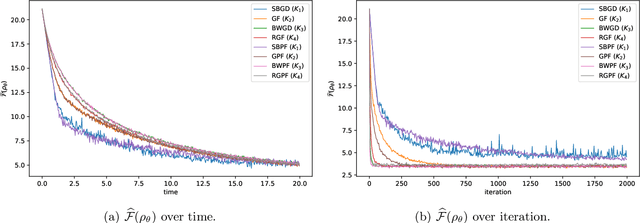
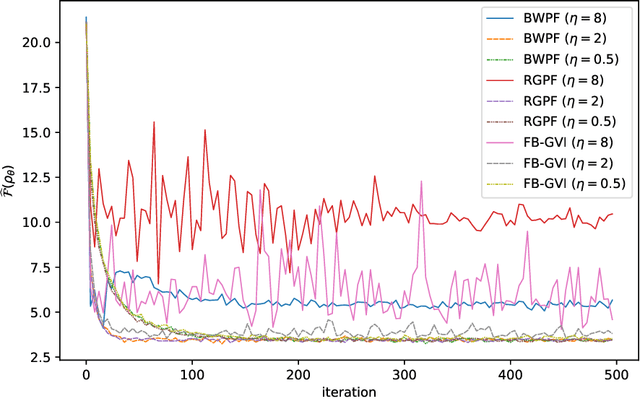
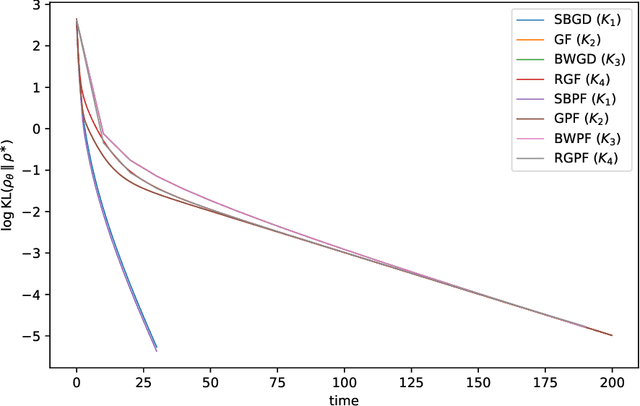
Towards Understanding the Dynamics of Gaussian--Stein Variational Gradient Descent

Stein Variational Gradient Descent (SVGD) is a nonparametric particle-based deterministic sampling algorithm. Despite its wide usage, understanding the theoretical properties of SVGD has remained a challenging problem. For sampling from a Gaussian target, the SVGD dynamics with a bilinear kernel will remain Gaussian as long as the initializer is Gaussian. Inspired by this fact, we undertake a detailed theoretical study of the Gaussian-SVGD, i.e., SVGD projected to the family of Gaussian distributions via the bilinear kernel, or equivalently Gaussian variational inference (GVI) with SVGD. We present a complete picture by considering both the mean-field PDE and discrete particle systems. When the target is strongly log-concave, the mean-field Gaussian-SVGD dynamics is proven to converge linearly to the Gaussian distribution closest to the target in KL divergence. In the finite-particle setting, there is both uniform in time convergence to the mean-field limit and linear convergence in time to the equilibrium if the target is Gaussian. In the general case, we propose a density-based and a particle-based implementation of the Gaussian-SVGD, and show that several recent algorithms for GVI, proposed from different perspectives, emerge as special cases of our unified framework. Interestingly, one of the new particle-based instance from this framework empirically outperforms existing approaches. Our results make concrete contributions towards obtaining a deeper understanding of both SVGD and GVI.