Large-Scale Quadratically Constrained Quadratic Program via Low-Discrepancy Sequences

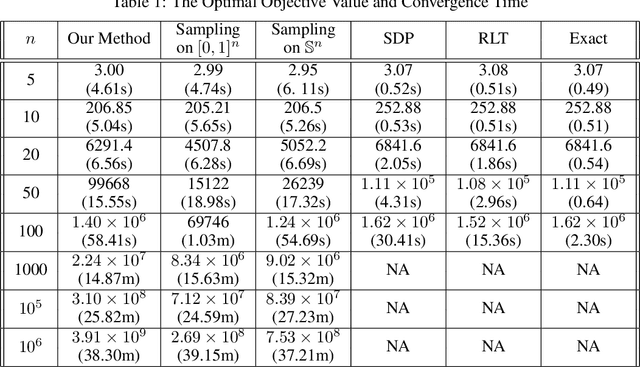
We consider the problem of solving a large-scale Quadratically Constrained Quadratic Program. Such problems occur naturally in many scientific and web applications. Although there are efficient methods which tackle this problem, they are mostly not scalable. In this paper, we develop a method that transforms the quadratic constraint into a linear form by sampling a set of low-discrepancy points. The transformed problem can then be solved by applying any state-of-the-art large-scale quadratic programming solvers. We show the convergence of our approximate solution to the true solution as well as some finite sample error bounds. Experimental results are also shown to prove scalability as well as improved quality of approximation in practice.

Constrained Multi-Slot Optimization for Ranking Recommendations

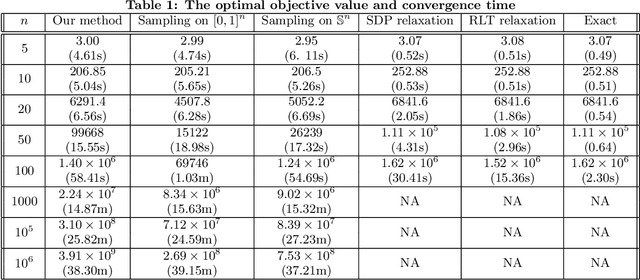
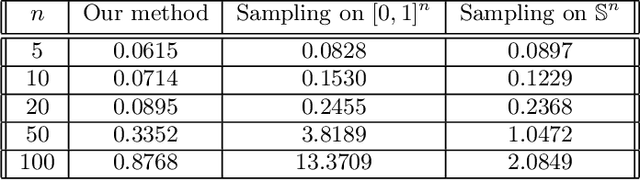
Ranking items to be recommended to users is one of the main problems in large scale social media applications. This problem can be set up as a multi-objective optimization problem to allow for trading off multiple, potentially conflicting objectives (that are driven by those items) against each other. Most previous approaches to this problem optimize for a single slot without considering the interaction effect of these items on one another. In this paper, we develop a constrained multi-slot optimization formulation, which allows for modeling interactions among the items on the different slots. We characterize the solution in terms of problem parameters and identify conditions under which an efficient solution is possible. The problem formulation results in a quadratically constrained quadratic program (QCQP). We provide an algorithm that gives us an efficient solution by relaxing the constraints of the QCQP minimally. Through simulated experiments, we show the benefits of modeling interactions in a multi-slot ranking context, and the speed and accuracy of our QCQP approximate solver against other state of the art methods.

Large scale multi-objective optimization: Theoretical and practical challenges

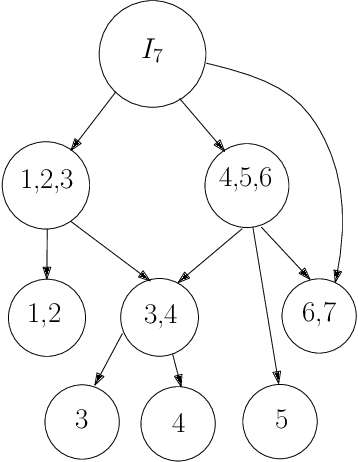
Multi-objective optimization (MOO) is a well-studied problem for several important recommendation problems. While multiple approaches have been proposed, in this work, we focus on using constrained optimization formulations (e.g., quadratic and linear programs) to formulate and solve MOO problems. This approach can be used to pick desired operating points on the trade-off curve between multiple objectives. It also works well for internet applications which serve large volumes of online traffic, by working with Lagrangian duality formulation to connect dual solutions (computed offline) with the primal solutions (computed online). We identify some key limitations of this approach -- namely the inability to handle user and item level constraints, scalability considerations and variance of dual estimates introduced by sampling processes. We propose solutions for each of the problems and demonstrate how through these solutions we significantly advance the state-of-the-art in this realm. Our proposed methods can exactly handle user and item (and other such local) constraints, achieve a $100\times$ scalability boost over existing packages in R and reduce variance of dual estimates by two orders of magnitude.

The Interplay Between Stability and Regret in Online Learning

This paper considers the stability of online learning algorithms and its implications for learnability (bounded regret). We introduce a novel quantity called {\em forward regret} that intuitively measures how good an online learning algorithm is if it is allowed a one-step look-ahead into the future. We show that given stability, bounded forward regret is equivalent to bounded regret. We also show that the existence of an algorithm with bounded regret implies the existence of a stable algorithm with bounded regret and bounded forward regret. The equivalence results apply to general, possibly non-convex problems. To the best of our knowledge, our analysis provides the first general connection between stability and regret in the online setting that is not restricted to a particular class of algorithms. Our stability-regret connection provides a simple recipe for analyzing regret incurred by any online learning algorithm. Using our framework, we analyze several existing online learning algorithms as well as the "approximate" versions of algorithms like RDA that solve an optimization problem at each iteration. Our proofs are simpler than existing analysis for the respective algorithms, show a clear trade-off between stability and forward regret, and provide tighter regret bounds in some cases. Furthermore, using our recipe, we analyze "approximate" versions of several algorithms such as follow-the-regularized-leader (FTRL) that requires solving an optimization problem at each step.

Smoothing Multivariate Performance Measures

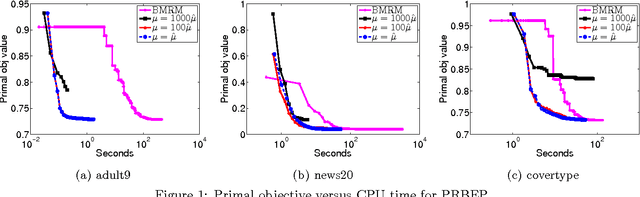
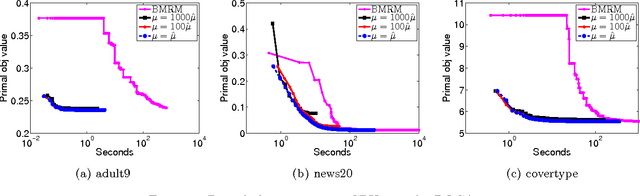
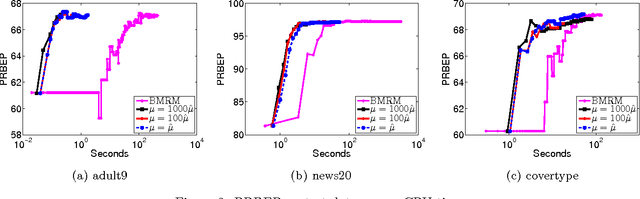
A Support Vector Method for multivariate performance measures was recently introduced by Joachims (2005). The underlying optimization problem is currently solved using cutting plane methods such as SVM-Perf and BMRM. One can show that these algorithms converge to an eta accurate solution in O(1/Lambda*e) iterations, where lambda is the trade-off parameter between the regularizer and the loss function. We present a smoothing strategy for multivariate performance scores, in particular precision/recall break-even point and ROCArea. When combined with Nesterov's accelerated gradient algorithm our smoothing strategy yields an optimization algorithm which converges to an eta accurate solution in O(min{1/e,1/sqrt(lambda*e)}) iterations. Furthermore, the cost per iteration of our scheme is the same as that of SVM-Perf and BMRM. Empirical evaluation on a number of publicly available datasets shows that our method converges significantly faster than cutting plane methods without sacrificing generalization ability.

Regularized Risk Minimization by Nesterov's Accelerated Gradient Methods: Algorithmic Extensions and Empirical Studies

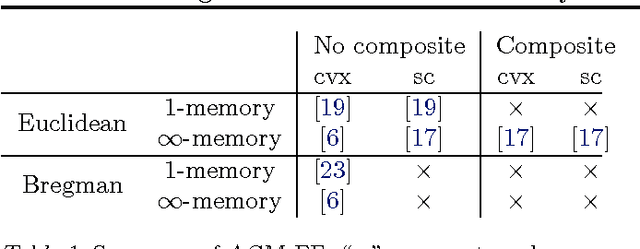
Nesterov's accelerated gradient methods (AGM) have been successfully applied in many machine learning areas. However, their empirical performance on training max-margin models has been inferior to existing specialized solvers. In this paper, we first extend AGM to strongly convex and composite objective functions with Bregman style prox-functions. Our unifying framework covers both the $\infty$-memory and 1-memory styles of AGM, tunes the Lipschiz constant adaptively, and bounds the duality gap. Then we demonstrate various ways to apply this framework of methods to a wide range of machine learning problems. Emphasis will be given on their rate of convergence and how to efficiently compute the gradient and optimize the models. The experimental results show that with our extensions AGM outperforms state-of-the-art solvers on max-margin models.

New Approximation Algorithms for Minimum Enclosing Convex Shapes

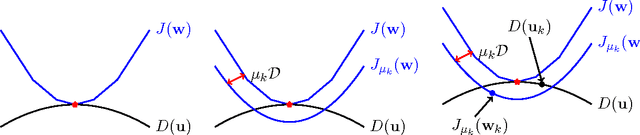
Given $n$ points in a $d$ dimensional Euclidean space, the Minimum Enclosing Ball (MEB) problem is to find the ball with the smallest radius which contains all $n$ points. We give a $O(nd\Qcal/\sqrt{\epsilon})$ approximation algorithm for producing an enclosing ball whose radius is at most $\epsilon$ away from the optimum (where $\Qcal$ is an upper bound on the norm of the points). This improves existing results using \emph{coresets}, which yield a $O(nd/\epsilon)$ greedy algorithm. Finding the Minimum Enclosing Convex Polytope (MECP) is a related problem wherein a convex polytope of a fixed shape is given and the aim is to find the smallest magnification of the polytope which encloses the given points. For this problem we present a $O(mnd\Qcal/\epsilon)$ approximation algorithm, where $m$ is the number of faces of the polytope. Our algorithms borrow heavily from convex duality and recently developed techniques in non-smooth optimization, and are in contrast with existing methods which rely on geometric arguments. In particular, we specialize the excessive gap framework of \citet{Nesterov05a} to obtain our results.

On the Finite Time Convergence of Cyclic Coordinate Descent Methods

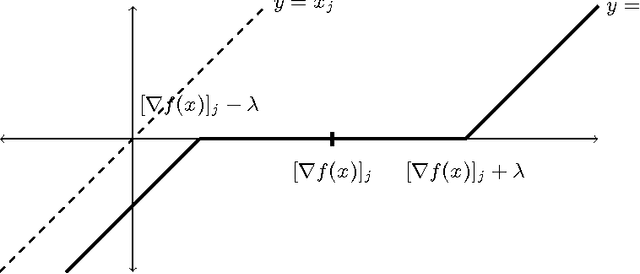
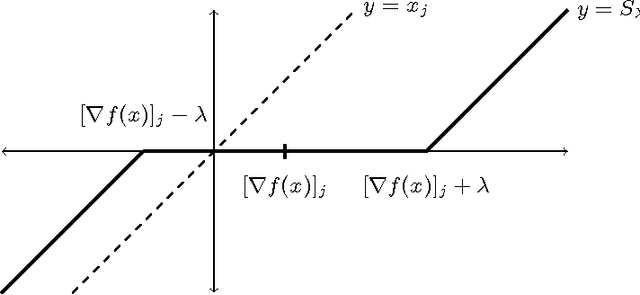
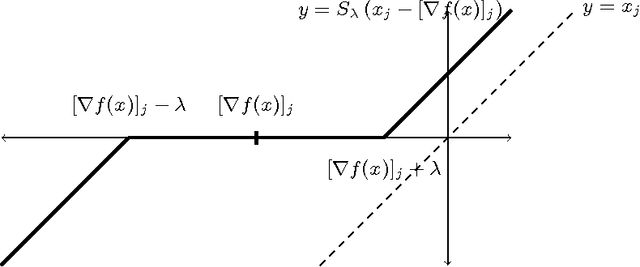
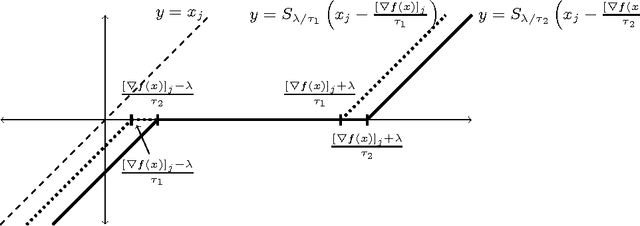
Cyclic coordinate descent is a classic optimization method that has witnessed a resurgence of interest in machine learning. Reasons for this include its simplicity, speed and stability, as well as its competitive performance on $\ell_1$ regularized smooth optimization problems. Surprisingly, very little is known about its finite time convergence behavior on these problems. Most existing results either just prove convergence or provide asymptotic rates. We fill this gap in the literature by proving $O(1/k)$ convergence rates (where $k$ is the iteration counter) for two variants of cyclic coordinate descent under an isotonicity assumption. Our analysis proceeds by comparing the objective values attained by the two variants with each other, as well as with the gradient descent algorithm. We show that the iterates generated by the cyclic coordinate descent methods remain better than those of gradient descent uniformly over time.

Faster Rates for training Max-Margin Markov Networks

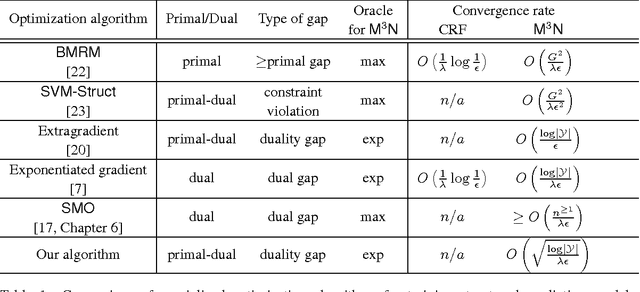
Structured output prediction is an important machine learning problem both in theory and practice, and the max-margin Markov network (\mcn) is an effective approach. All state-of-the-art algorithms for optimizing \mcn\ objectives take at least $O(1/\epsilon)$ number of iterations to find an $\epsilon$ accurate solution. Recent results in structured optimization suggest that faster rates are possible by exploiting the structure of the objective function. Towards this end \citet{Nesterov05} proposed an excessive gap reduction technique based on Euclidean projections which converges in $O(1/\sqrt{\epsilon})$ iterations on strongly convex functions. Unfortunately when applied to \mcn s, this approach does not admit graphical model factorization which, as in many existing algorithms, is crucial for keeping the cost per iteration tractable. In this paper, we present a new excessive gap reduction technique based on Bregman projections which admits graphical model factorization naturally, and converges in $O(1/\sqrt{\epsilon})$ iterations. Compared with existing algorithms, the convergence rate of our method has better dependence on $\epsilon$ and other parameters of the problem, and can be easily kernelized.

Lower Bounds for BMRM and Faster Rates for Training SVMs

Regularized risk minimization with the binary hinge loss and its variants lies at the heart of many machine learning problems. Bundle methods for regularized risk minimization (BMRM) and the closely related SVMStruct are considered the best general purpose solvers to tackle this problem. It was recently shown that BMRM requires $O(1/\epsilon)$ iterations to converge to an $\epsilon$ accurate solution. In the first part of the paper we use the Hadamard matrix to construct a regularized risk minimization problem and show that these rates cannot be improved. We then show how one can exploit the structure of the objective function to devise an algorithm for the binary hinge loss which converges to an $\epsilon$ accurate solution in $O(1/\sqrt{\epsilon})$ iterations.