On the Finite Time Convergence of Cyclic Coordinate Descent Methods
Paper and Code
May 12, 2010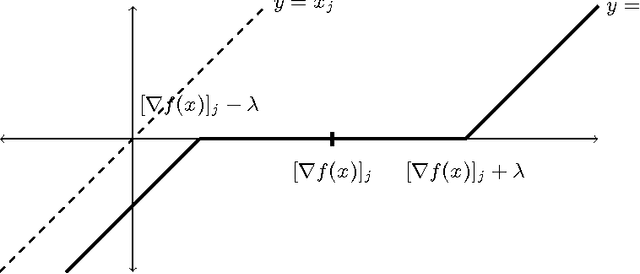
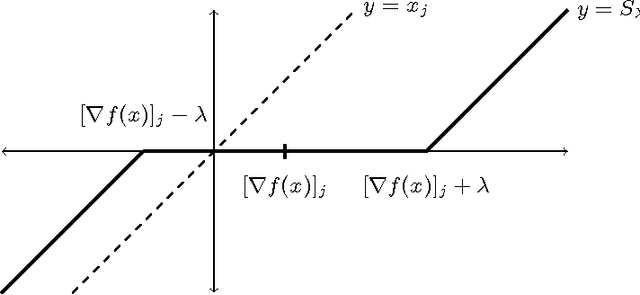
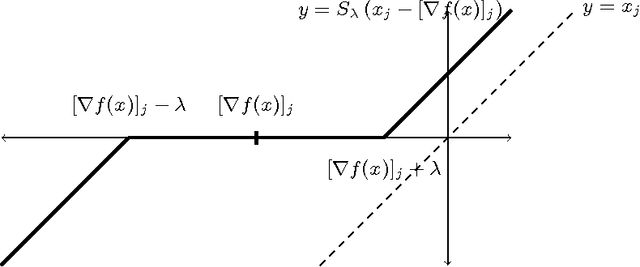
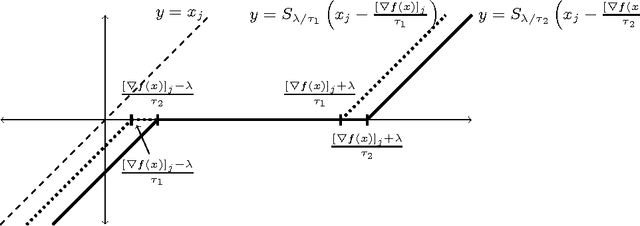
Cyclic coordinate descent is a classic optimization method that has witnessed a resurgence of interest in machine learning. Reasons for this include its simplicity, speed and stability, as well as its competitive performance on $\ell_1$ regularized smooth optimization problems. Surprisingly, very little is known about its finite time convergence behavior on these problems. Most existing results either just prove convergence or provide asymptotic rates. We fill this gap in the literature by proving $O(1/k)$ convergence rates (where $k$ is the iteration counter) for two variants of cyclic coordinate descent under an isotonicity assumption. Our analysis proceeds by comparing the objective values attained by the two variants with each other, as well as with the gradient descent algorithm. We show that the iterates generated by the cyclic coordinate descent methods remain better than those of gradient descent uniformly over time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge