Faster Rates for training Max-Margin Markov Networks
Paper and Code
Mar 06, 2010
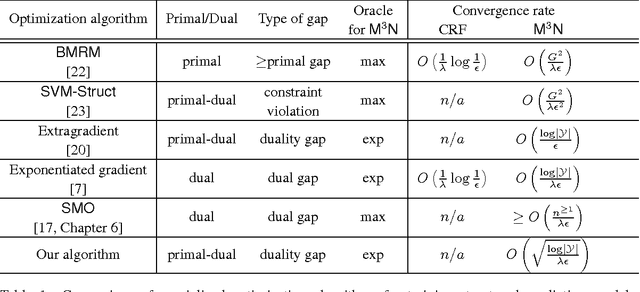

Structured output prediction is an important machine learning problem both in theory and practice, and the max-margin Markov network (\mcn) is an effective approach. All state-of-the-art algorithms for optimizing \mcn\ objectives take at least $O(1/\epsilon)$ number of iterations to find an $\epsilon$ accurate solution. Recent results in structured optimization suggest that faster rates are possible by exploiting the structure of the objective function. Towards this end \citet{Nesterov05} proposed an excessive gap reduction technique based on Euclidean projections which converges in $O(1/\sqrt{\epsilon})$ iterations on strongly convex functions. Unfortunately when applied to \mcn s, this approach does not admit graphical model factorization which, as in many existing algorithms, is crucial for keeping the cost per iteration tractable. In this paper, we present a new excessive gap reduction technique based on Bregman projections which admits graphical model factorization naturally, and converges in $O(1/\sqrt{\epsilon})$ iterations. Compared with existing algorithms, the convergence rate of our method has better dependence on $\epsilon$ and other parameters of the problem, and can be easily kernelized.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge