Regularized Risk Minimization by Nesterov's Accelerated Gradient Methods: Algorithmic Extensions and Empirical Studies
Paper and Code
Nov 01, 2010
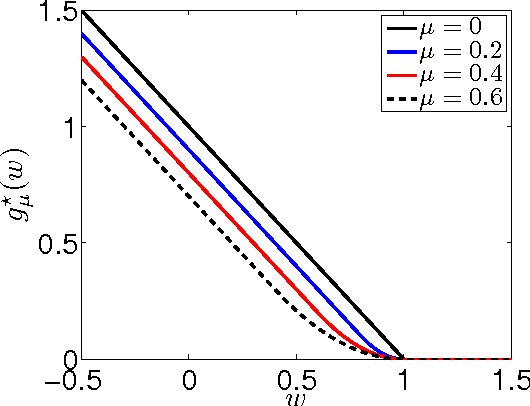
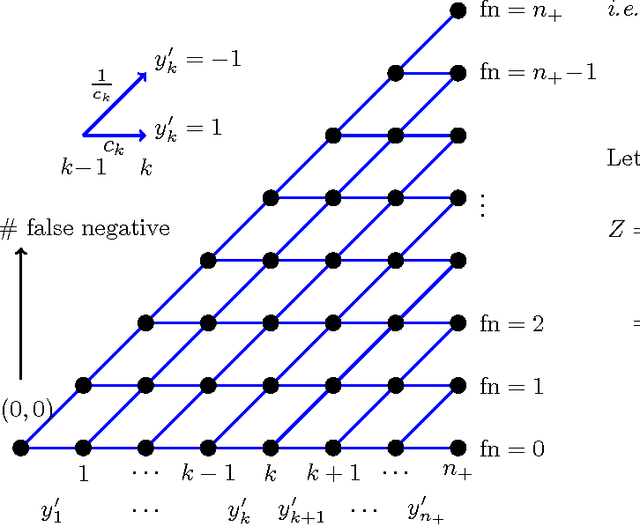
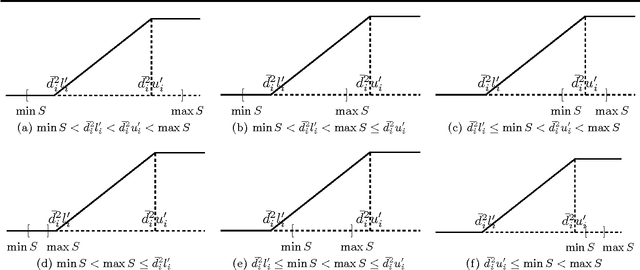
Nesterov's accelerated gradient methods (AGM) have been successfully applied in many machine learning areas. However, their empirical performance on training max-margin models has been inferior to existing specialized solvers. In this paper, we first extend AGM to strongly convex and composite objective functions with Bregman style prox-functions. Our unifying framework covers both the $\infty$-memory and 1-memory styles of AGM, tunes the Lipschiz constant adaptively, and bounds the duality gap. Then we demonstrate various ways to apply this framework of methods to a wide range of machine learning problems. Emphasis will be given on their rate of convergence and how to efficiently compute the gradient and optimize the models. The experimental results show that with our extensions AGM outperforms state-of-the-art solvers on max-margin models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge