The Entire Quantile Path of a Risk-Agnostic SVM Classifier

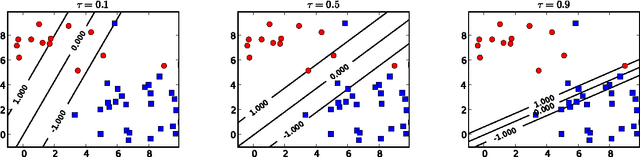
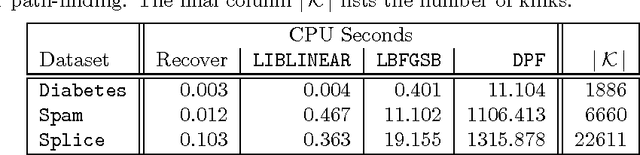
A quantile binary classifier uses the rule: Classify x as +1 if P(Y = 1|X = x) >= t, and as -1 otherwise, for a fixed quantile parameter t {[0, 1]. It has been shown that Support Vector Machines (SVMs) in the limit are quantile classifiers with t = 1/2 . In this paper, we show that by using asymmetric cost of misclassification SVMs can be appropriately extended to recover, in the limit, the quantile binary classifier for any t. We then present a principled algorithm to solve the extended SVM classifier for all values of t simultaneously. This has two implications: First, one can recover the entire conditional distribution P(Y = 1|X = x) = t for t {[0, 1]. Second, we can build a risk-agnostic SVM classifier where the cost of misclassification need not be known apriori. Preliminary numerical experiments show the effectiveness of the proposed algorithm.

Smoothing Multivariate Performance Measures

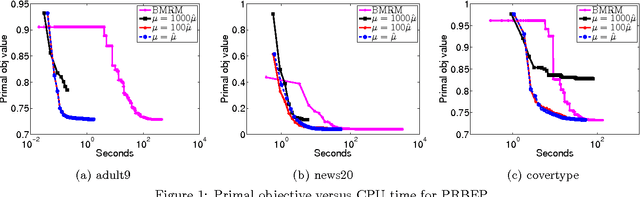
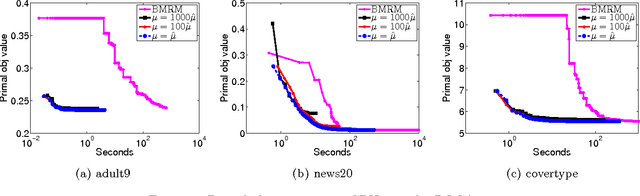
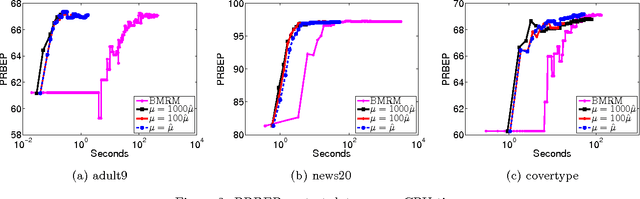
A Support Vector Method for multivariate performance measures was recently introduced by Joachims (2005). The underlying optimization problem is currently solved using cutting plane methods such as SVM-Perf and BMRM. One can show that these algorithms converge to an eta accurate solution in O(1/Lambda*e) iterations, where lambda is the trade-off parameter between the regularizer and the loss function. We present a smoothing strategy for multivariate performance scores, in particular precision/recall break-even point and ROCArea. When combined with Nesterov's accelerated gradient algorithm our smoothing strategy yields an optimization algorithm which converges to an eta accurate solution in O(min{1/e,1/sqrt(lambda*e)}) iterations. Furthermore, the cost per iteration of our scheme is the same as that of SVM-Perf and BMRM. Empirical evaluation on a number of publicly available datasets shows that our method converges significantly faster than cutting plane methods without sacrificing generalization ability.