The Entire Quantile Path of a Risk-Agnostic SVM Classifier
Paper and Code
May 09, 2012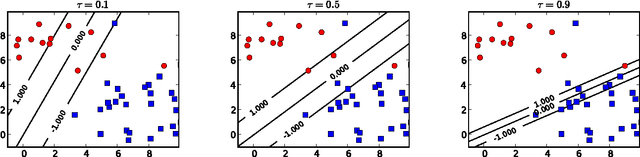
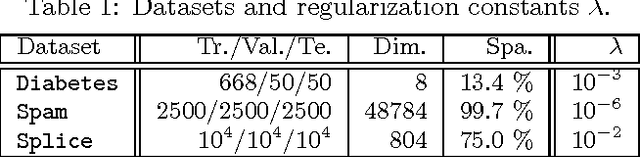
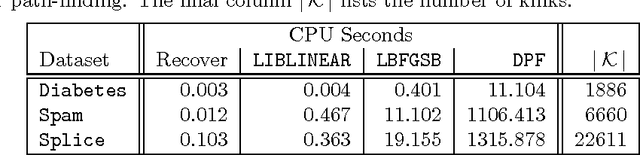

A quantile binary classifier uses the rule: Classify x as +1 if P(Y = 1|X = x) >= t, and as -1 otherwise, for a fixed quantile parameter t {[0, 1]. It has been shown that Support Vector Machines (SVMs) in the limit are quantile classifiers with t = 1/2 . In this paper, we show that by using asymmetric cost of misclassification SVMs can be appropriately extended to recover, in the limit, the quantile binary classifier for any t. We then present a principled algorithm to solve the extended SVM classifier for all values of t simultaneously. This has two implications: First, one can recover the entire conditional distribution P(Y = 1|X = x) = t for t {[0, 1]. Second, we can build a risk-agnostic SVM classifier where the cost of misclassification need not be known apriori. Preliminary numerical experiments show the effectiveness of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge