On the design of scalable, high-precision spherical-radial Fourier features

Approximation using Fourier features is a popular technique for scaling kernel methods to large-scale problems, with myriad applications in machine learning and statistics. This method replaces the integral representation of a shift-invariant kernel with a sum using a quadrature rule. The design of the latter is meant to reduce the number of features required for high-precision approximation. Specifically, for the squared exponential kernel, one must design a quadrature rule that approximates the Gaussian measure on $\mathbb{R}^d$. Previous efforts in this line of research have faced difficulties in higher dimensions. We introduce a new family of quadrature rules that accurately approximate the Gaussian measure in higher dimensions by exploiting its isotropy. These rules are constructed as a tensor product of a radial quadrature rule and a spherical quadrature rule. Compared to previous work, our approach leverages a thorough analysis of the approximation error, which suggests natural choices for both the radial and spherical components. We demonstrate that this family of Fourier features yields improved approximation bounds.

Nonlinear Bayesian optimal experimental design using logarithmic Sobolev inequalities

We study the problem of selecting $k$ experiments from a larger candidate pool, where the goal is to maximize mutual information (MI) between the selected subset and the underlying parameters. Finding the exact solution is to this combinatorial optimization problem is computationally costly, not only due to the complexity of the combinatorial search but also the difficulty of evaluating MI in nonlinear/non-Gaussian settings. We propose greedy approaches based on new computationally inexpensive lower bounds for MI, constructed via log-Sobolev inequalities. We demonstrate that our method outperforms random selection strategies, Gaussian approximations, and nested Monte Carlo (NMC) estimators of MI in various settings, including optimal design for nonlinear models with non-additive noise.

Sketch and shift: a robust decoder for compressive clustering

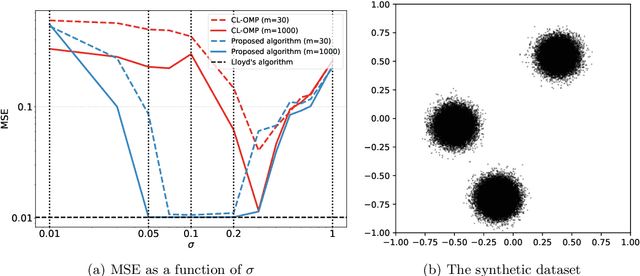
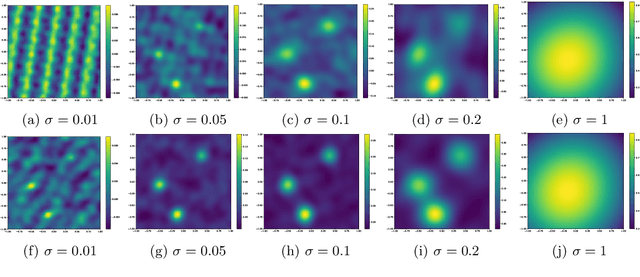
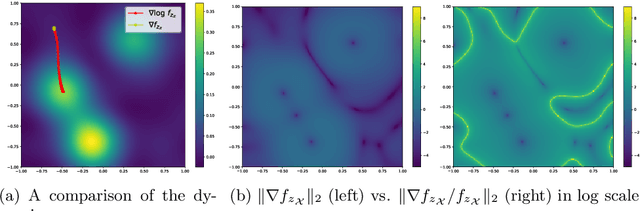
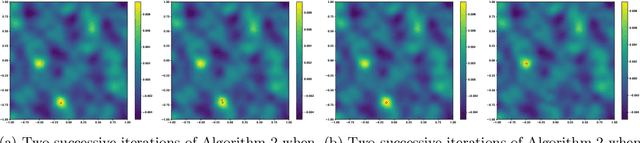
Compressive learning is an emerging approach to drastically reduce the memory footprint of large-scale learning, by first summarizing a large dataset into a low-dimensional sketch vector, and then decoding from this sketch the latent information needed for learning. In light of recent progress on information preservation guarantees for sketches based on random features, a major objective is to design easy-to-tune algorithms (called decoders) to robustly and efficiently extract this information. To address the underlying non-convex optimization problems, various heuristics have been proposed. In the case of compressive clustering, the standard heuristic is CL-OMPR, a variant of sliding Frank-Wolfe. Yet, CL-OMPR is hard to tune, and the examination of its robustness was overlooked. In this work, we undertake a scrutinized examination of CL-OMPR to circumvent its limitations. In particular, we show how this algorithm can fail to recover the clusters even in advantageous scenarios. To gain insight, we show how the deficiencies of this algorithm can be attributed to optimization difficulties related to the structure of a correlation function appearing at core steps of the algorithm. To address these limitations, we propose an alternative decoder offering substantial improvements over CL-OMPR. Its design is notably inspired from the mean shift algorithm, a classic approach to detect the local maxima of kernel density estimators. The proposed algorithm can extract clustering information from a sketch of the MNIST dataset that is 10 times smaller than previously.

Revisiting RIP guarantees for sketching operators on mixture models

In the context of sketching for compressive mixture modeling, we revisit existing proofs of the Restricted Isometry Property of sketching operators with respect to certain mixtures models. After examining the shortcomings of existing guarantees, we propose an alternative analysis that circumvents the need to assume importance sampling when drawing random Fourier features to build random sketching operators. Our analysis is based on new deterministic bounds on the restricted isometry constant that depend solely on the set of frequencies used to define the sketching operator; then we leverage these bounds to establish concentration inequalities for random sketching operators that lead to the desired RIP guarantees. Our analysis also opens the door to theoretical guarantees for structured sketching with frequencies associated to fast random linear operators.

Signal reconstruction using determinantal sampling

We study the approximation of a square-integrable function from a finite number of evaluations on a random set of nodes according to a well-chosen distribution. This is particularly relevant when the function is assumed to belong to a reproducing kernel Hilbert space (RKHS). This work proposes to combine several natural finite-dimensional approximations based two possible probability distributions of nodes. These distributions are related to determinantal point processes, and use the kernel of the RKHS to favor RKHS-adapted regularity in the random design. While previous work on determinantal sampling relied on the RKHS norm, we prove mean-square guarantees in $L^2$ norm. We show that determinantal point processes and mixtures thereof can yield fast convergence rates. Our results also shed light on how the rate changes as more smoothness is assumed, a phenomenon known as superconvergence. Besides, determinantal sampling generalizes i.i.d. sampling from the Christoffel function which is standard in the literature. More importantly, determinantal sampling guarantees the so-called instance optimality property for a smaller number of function evaluations than i.i.d. sampling.

Kernel interpolation with continuous volume sampling

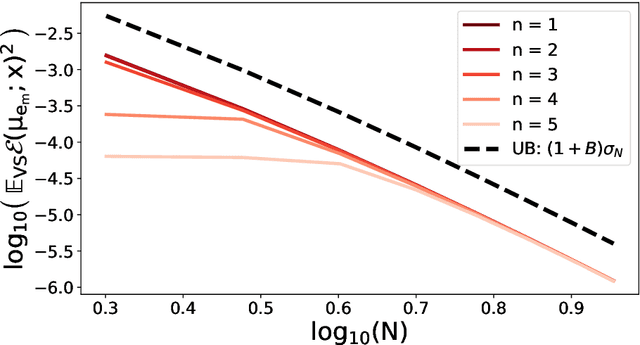
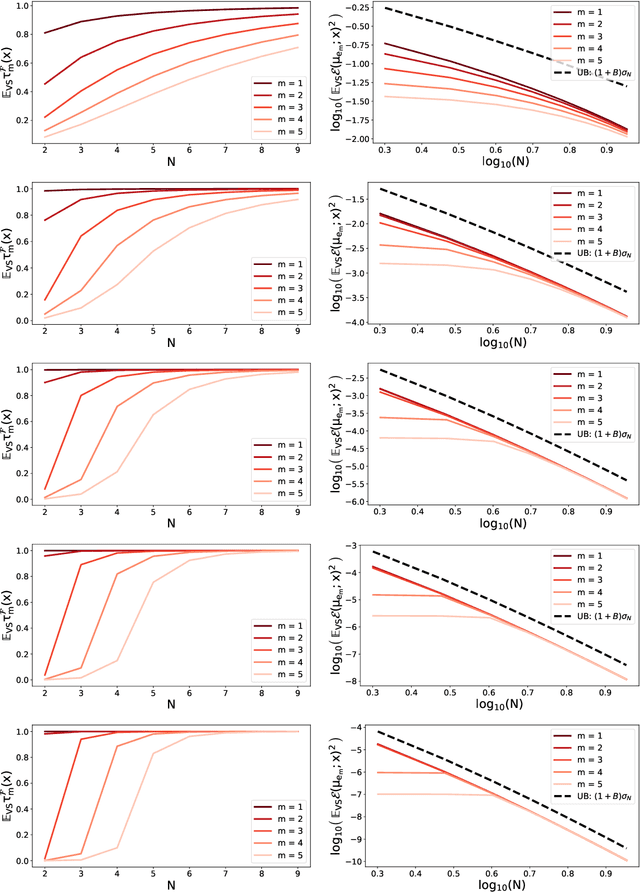
A fundamental task in kernel methods is to pick nodes and weights, so as to approximate a given function from an RKHS by the weighted sum of kernel translates located at the nodes. This is the crux of kernel density estimation, kernel quadrature, or interpolation from discrete samples. Furthermore, RKHSs offer a convenient mathematical and computational framework. We introduce and analyse continuous volume sampling (VS), the continuous counterpart -- for choosing node locations -- of a discrete distribution introduced in (Deshpande & Vempala, 2006). Our contribution is theoretical: we prove almost optimal bounds for interpolation and quadrature under VS. While similar bounds already exist for some specific RKHSs using ad-hoc node constructions, VS offers bounds that apply to any Mercer kernel and depend on the spectrum of the associated integration operator. We emphasize that, unlike previous randomized approaches that rely on regularized leverage scores or determinantal point processes, evaluating the pdf of VS only requires pointwise evaluations of the kernel. VS is thus naturally amenable to MCMC samplers.

Kernel quadrature with DPPs

We study quadrature rules for functions living in an RKHS, using nodes sampled from a projection determinantal point process (DPP). DPPs are parametrized by a kernel, and we use a truncated and saturated version of the RKHS kernel. This natural link between the two kernels, along with DPP machinery, leads to relatively tight bounds on the quadrature error, that depend on the spectrum of the RKHS kernel. Finally, we experimentally compare DPPs to existing kernel-based quadratures such as herding, Bayesian quadrature, or continuous leverage score sampling. Numerical results confirm the interest of DPPs, and even suggest faster rates than our bounds in particular cases.

A determinantal point process for column subset selection

Dimensionality reduction is a first step of many machine learning pipelines. Two popular approaches are principal component analysis, which projects onto a small number of well chosen but non-interpretable directions, and feature selection, which selects a small number of the original features. Feature selection can be abstracted as a numerical linear algebra problem called the column subset selection problem (CSSP). CSSP corresponds to selecting the best subset of columns of a matrix $X \in \mathbb{R}^{N \times d}$, where \emph{best} is often meant in the sense of minimizing the approximation error, i.e., the norm of the residual after projection of $X$ onto the space spanned by the selected columns. Such an optimization over subsets of $\{1,\dots,d\}$ is usually impractical. One workaround that has been vastly explored is to resort to polynomial-cost, random subset selection algorithms that favor small values of this approximation error. We propose such a randomized algorithm, based on sampling from a projection determinantal point process (DPP), a repulsive distribution over a fixed number $k$ of indices $\{1,\dots,d\}$ that favors diversity among the selected columns. We give bounds on the ratio of the expected approximation error for this DPP over the optimal error of PCA. These bounds improve over the state-of-the-art bounds of \emph{volume sampling} when some realistic structural assumptions are satisfied for $X$. Numerical experiments suggest that our bounds are tight, and that our algorithms have comparable performance with the \emph{double phase} algorithm, often considered to be the practical state-of-the-art. Column subset selection with DPPs thus inherits the best of both worlds: good empirical performance and tight error bounds.