Ensemble Kalman-Bucy filtering for nonlinear model predictive control

We consider the problem of optimal control for partially observed dynamical systems. Despite its prevalence in practical applications, there are still very few algorithms available, which take uncertainties in the current state estimates and future observations into account. In other words, most current approaches separate state estimation from the optimal control problem. In this paper, we extend the popular ensemble Kalman filter to receding horizon optimal control problems in the spirit of nonlinear model predictive control. We provide an interacting particle approximation to the forward-backward stochastic differential equations arising from Pontryagin's maximum principle with the forward stochastic differential equation provided by the time-continuous ensemble Kalman-Bucy filter equations. The receding horizon control laws are approximated as linear and are continuously updated as in nonlinear model predictive control. We illustrate the performance of the proposed methodology for an inverted pendulum example.

Localized Schrödinger Bridge Sampler

We consider the generative problem of sampling from an unknown distribution for which only a sufficiently large number of training samples are available. In this paper, we build on previous work combining Schr\"odinger bridges and Langevin dynamics. A key bottleneck of this approach is the exponential dependence of the required training samples on the dimension, $d$, of the ambient state space. We propose a localization strategy which exploits conditional independence of conditional expectation values. Localization thus replaces a single high-dimensional Schr\"odinger bridge problem by $d$ low-dimensional Schr\"odinger bridge problems over the available training samples. As for the original approach, the localized sampler is stable and geometric ergodic. The sampler also naturally extends to conditional sampling and to Bayesian inference. We demonstrate the performance of our proposed scheme through experiments on a Gaussian problem with increasing dimensions and on a stochastic subgrid-scale parametrization conditional sampling problem.

Efficient, Multimodal, and Derivative-Free Bayesian Inference With Fisher-Rao Gradient Flows

In this paper, we study efficient approximate sampling for probability distributions known up to normalization constants. We specifically focus on a problem class arising in Bayesian inference for large-scale inverse problems in science and engineering applications. The computational challenges we address with the proposed methodology are: (i) the need for repeated evaluations of expensive forward models; (ii) the potential existence of multiple modes; and (iii) the fact that gradient of, or adjoint solver for, the forward model might not be feasible. While existing Bayesian inference methods meet some of these challenges individually, we propose a framework that tackles all three systematically. Our approach builds upon the Fisher-Rao gradient flow in probability space, yielding a dynamical system for probability densities that converges towards the target distribution at a uniform exponential rate. This rapid convergence is advantageous for the computational burden outlined in (i). We apply Gaussian mixture approximations with operator splitting techniques to simulate the flow numerically; the resulting approximation can capture multiple modes thus addressing (ii). Furthermore, we employ the Kalman methodology to facilitate a derivative-free update of these Gaussian components and their respective weights, addressing the issue in (iii). The proposed methodology results in an efficient derivative-free sampler flexible enough to handle multi-modal distributions: Gaussian Mixture Kalman Inversion (GMKI). The effectiveness of GMKI is demonstrated both theoretically and numerically in several experiments with multimodal target distributions, including proof-of-concept and two-dimensional examples, as well as a large-scale application: recovering the Navier-Stokes initial condition from solution data at positive times.

Stable generative modeling using diffusion maps

We consider the problem of sampling from an unknown distribution for which only a sufficiently large number of training samples are available. Such settings have recently drawn considerable interest in the context of generative modelling. In this paper, we propose a generative model combining diffusion maps and Langevin dynamics. Diffusion maps are used to approximate the drift term from the available training samples, which is then implemented in a discrete-time Langevin sampler to generate new samples. By setting the kernel bandwidth to match the time step size used in the unadjusted Langevin algorithm, our method effectively circumvents any stability issues typically associated with time-stepping stiff stochastic differential equations. More precisely, we introduce a novel split-step scheme, ensuring that the generated samples remain within the convex hull of the training samples. Our framework can be naturally extended to generate conditional samples. We demonstrate the performance of our proposed scheme through experiments on synthetic datasets with increasing dimensions and on a stochastic subgrid-scale parametrization conditional sampling problem.

Sampling via Gradient Flows in the Space of Probability Measures

Sampling a target probability distribution with an unknown normalization constant is a fundamental challenge in computational science and engineering. Recent work shows that algorithms derived by considering gradient flows in the space of probability measures open up new avenues for algorithm development. This paper makes three contributions to this sampling approach by scrutinizing the design components of such gradient flows. Any instantiation of a gradient flow for sampling needs an energy functional and a metric to determine the flow, as well as numerical approximations of the flow to derive algorithms. Our first contribution is to show that the Kullback-Leibler divergence, as an energy functional, has the unique property (among all f-divergences) that gradient flows resulting from it do not depend on the normalization constant of the target distribution. Our second contribution is to study the choice of metric from the perspective of invariance. The Fisher-Rao metric is known as the unique choice (up to scaling) that is diffeomorphism invariant. As a computationally tractable alternative, we introduce a relaxed, affine invariance property for the metrics and gradient flows. In particular, we construct various affine invariant Wasserstein and Stein gradient flows. Affine invariant gradient flows are shown to behave more favorably than their non-affine-invariant counterparts when sampling highly anisotropic distributions, in theory and by using particle methods. Our third contribution is to study, and develop efficient algorithms based on Gaussian approximations of the gradient flows; this leads to an alternative to particle methods. We establish connections between various Gaussian approximate gradient flows, discuss their relation to gradient methods arising from parametric variational inference, and study their convergence properties both theoretically and numerically.

Affine Invariant Ensemble Transform Methods to Improve Predictive Uncertainty in ReLU Networks

We consider the problem of performing Bayesian inference for logistic regression using appropriate extensions of the ensemble Kalman filter. Two interacting particle systems are proposed that sample from an approximate posterior and prove quantitative convergence rates of these interacting particle systems to their mean-field limit as the number of particles tends to infinity. Furthermore, we apply these techniques and examine their effectiveness as methods of Bayesian approximation for quantifying predictive uncertainty in ReLU networks.

Gradient Flows for Sampling: Mean-Field Models, Gaussian Approximations and Affine Invariance

Sampling a probability distribution with an unknown normalization constant is a fundamental problem in computational science and engineering. This task may be cast as an optimization problem over all probability measures, and an initial distribution can be evolved to the desired minimizer dynamically via gradient flows. Mean-field models, whose law is governed by the gradient flow in the space of probability measures, may also be identified; particle approximations of these mean-field models form the basis of algorithms. The gradient flow approach is also the basis of algorithms for variational inference, in which the optimization is performed over a parameterized family of probability distributions such as Gaussians, and the underlying gradient flow is restricted to the parameterized family. By choosing different energy functionals and metrics for the gradient flow, different algorithms with different convergence properties arise. In this paper, we concentrate on the Kullback-Leibler divergence after showing that, up to scaling, it has the unique property that the gradient flows resulting from this choice of energy do not depend on the normalization constant. For the metrics, we focus on variants of the Fisher-Rao, Wasserstein, and Stein metrics; we introduce the affine invariance property for gradient flows, and their corresponding mean-field models, determine whether a given metric leads to affine invariance, and modify it to make it affine invariant if it does not. We study the resulting gradient flows in both probability density space and Gaussian space. The flow in the Gaussian space may be understood as a Gaussian approximation of the flow. We demonstrate that the Gaussian approximation based on the metric and through moment closure coincide, establish connections between them, and study their long-time convergence properties showing the advantages of affine invariance.

Infinite-Dimensional Diffusion Models for Function Spaces

We define diffusion-based generative models in infinite dimensions, and apply them to the generative modeling of functions. By first formulating such models in the infinite-dimensional limit and only then discretizing, we are able to obtain a sampling algorithm that has \emph{dimension-free} bounds on the distance from the sample measure to the target measure. Furthermore, we propose a new way to perform conditional sampling in an infinite-dimensional space and show that our approach outperforms previously suggested procedures.

Combining machine learning and data assimilation to forecast dynamical systems from noisy partial observations

We present a supervised learning method to learn the propagator map of a dynamical system from partial and noisy observations. In our computationally cheap and easy-to-implement framework a neural network consisting of random feature maps is trained sequentially by incoming observations within a data assimilation procedure. By employing Takens' embedding theorem, the network is trained on delay coordinates. We show that the combination of random feature maps and data assimilation, called RAFDA, outperforms standard random feature maps for which the dynamics is learned using batch data.

Learning effective stochastic differential equations from microscopic simulations: combining stochastic numerics and deep learning

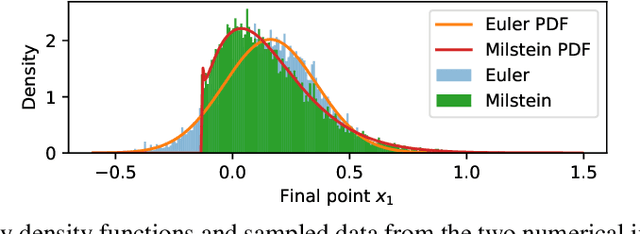
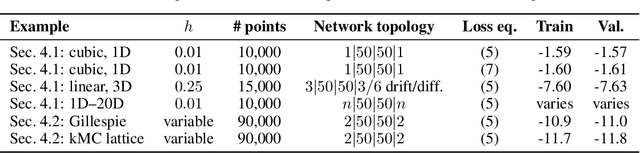
We identify effective stochastic differential equations (SDE) for coarse observables of fine-grained particle- or agent-based simulations; these SDE then provide coarse surrogate models of the fine scale dynamics. We approximate the drift and diffusivity functions in these effective SDE through neural networks, which can be thought of as effective stochastic ResNets. The loss function is inspired by, and embodies, the structure of established stochastic numerical integrators (here, Euler-Maruyama and Milstein); our approximations can thus benefit from error analysis of these underlying numerical schemes. They also lend themselves naturally to "physics-informed" gray-box identification when approximate coarse models, such as mean field equations, are available. Our approach does not require long trajectories, works on scattered snapshot data, and is designed to naturally handle different time steps per snapshot. We consider both the case where the coarse collective observables are known in advance, as well as the case where they must be found in a data-driven manner.